|
#1 - 24-10-2014 01:03:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#2 - 26-10-2014 23:39:03
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Gâeau 82
En fait je ne comprends pas tes dessins, les flèches rouges symbolisent-elles le déplacement du bâton? Si oui dans quel sens faut-il lire ton enchaînement? 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#3 - 27-10-2014 00:28:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteeau 82
Il me semble que personne n'a compris le problème , la formulation n'était donc vraiment pas claire .
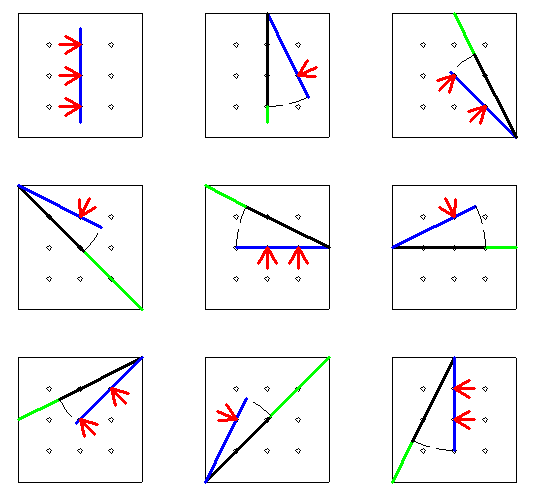
Imaginons une grille cloutée infinie dont les clous sont les points à coordonnées entières d'un repère orthonormé . Entre les clous , on pose une tige parallèle à l'un des axes de coordonnées et on essaie de la retourner sans traverser les clous . Sur une grille infinie , c'est toujours possible mais si on limite le cadre des opérations , la manœuvre devient plus délicate .
Vasimolo
PS : flèches rouges = point de blocage . Segments verts = glissement avant rotation .
PPS : c'est un problème personnel donc pas de solution garantie sans faille 
#4 - 27-10-2014 17:17:12
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
hâteau 82
OK c'est bon j'ai compris, je vais y réfléchir !
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#5 - 01-11-2014 11:34:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteu 82
Pour ne pas laisser en plan la question...
Je trouve une formule générale approximative N=y(2L-rac(x²+y²)/rac(x²+y²)
On cherche le max de N pour cette formule.
Pour L=40, je trouve un max de N avec x=1 et y=5 de 74, qu'il faut corriger en N=75.
(x,y) sont les dimensions d'un triangle rectangle placé dans le milieu du carré, cas le plus défavorable.
#6 - 01-11-2014 19:07:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâteai 82
Il faudrait que tu détailles un peu Nodgim ( tu devrais savoir que j'ai une toute petite tête et aucune imagination  ) )
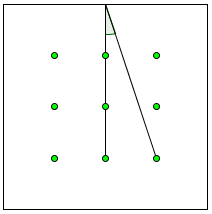
Pour une grille de taille 3 la plus grande baguette que l'on peut retourner est de taille 2 :
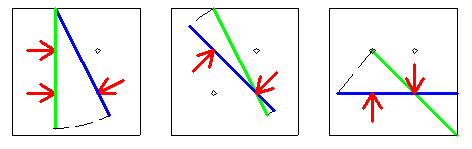
Il y a sûrement un moyen de rendre les manœuvres compréhensibles .
En tout cas merci de t'intéresser au problème qui ne mobilise pas les foules .
Vasimolo
#7 - 02-11-2014 09:07:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteau 28
Un peu compliqué à développer pour l'instant. J'ai lancé cette valeur de 75 en fonction de mon idée. J'imagine que tu as dû aussi de ton coté trouver une valeur, j'aimerais bien la connaitre.
#8 - 02-11-2014 11:50:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtau 82
Bonjour Nodgim
Je n'ai pas de valeur à te proposer mais je peux te dire ce que j'avais commencé à faire .
On prend le problème à l'envers c'est à dire qu'on cherche la taille t(n) de la plus grande aiguille que l'on peut retourner dans une grille cloutée de côté n . T(n) est clairement croissante et t(mn)=<mt(n) car multiplier la taille de la grille revient à ajouter des clous .
Sauf erreur , les premières valeurs de t(n) : 1 ; 2 ; 2 ; 2V2 ; 3 ; 4 ; ...
Toujours sauf erreur il semblerait que les blocages de l'aiguille se fassent toujours sur les lignes horizontales , verticales ou diagonales . Je me demande d'ailleurs si le blocage sur la diagonale pour n=4 n'est pas exceptionnel .
Ca fait tout de même beaucoup de points d'interrogations 
Remarque : A priori ta proposition n'est pas en contradiction avec la fonction t :
t(75) = t(15 X 5)=< 15 X t(5) = 45 .
Il reste encore pas mal de grain à moudre .
Vasimolo
PS : tout ça est un peu pénible à lire mais Latex a encore rendu l'âme .
#9 - 02-11-2014 12:25:49
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
#10 - 02-11-2014 12:49:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteaau 82
Comme j'aimerais que ce soit aussi simple 
Pour l'exemple que tu as choisi , tu devrais pouvoir retourner une baguette de taille V(10)=3,16...
Je crois que c'est un problème difficile mais c'est vraiment sympa de participer 
Vasimolo
#11 - 15-11-2014 15:23:53
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâtteau 82
Il faut arriver à faire 1/8 de tour (45°), et c'est gagné.
La suite s'obtient par symétrie.
On peut essayer avec des baguettes de longueurs 2, 3, 4, etc...
et regarder si OEIS donne la séquence des dimensions nécessaires
d'après les premières valeurs trouvées.
#12 - 15-11-2014 17:24:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâeau 82
Je ne pense pas qu'un quart de tour suffise , la sortie d'une position horizontale étant justement l'une des plus délicates en démarrant verticalement . J'avais essayé l'OEIS sans succès avec les carrés des valeurs proposées dans le message #8 : il s'agit donc d'une suite inédite .
Vasimolo
#13 - 15-11-2014 19:54:41
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
gâreau 82
Vasimolo a écrit:Sauf erreur , les premières valeurs de t(n) : 1 ; 2 ; 2 ; 2V2 ; 3 ; 4 ; ...
Sauf erreur aussi , ces valeurs sont fausses.
Grille de dimension 1 : barre de longueur 1 OK
Grille de dimension 2 : barre de longueur 2 OK
Grille de dimension 3 : barre de longueur 2 Bah, non, 2 rac(2) ça passe
Grille de dimension 4 : Pas encore réfléchi mais j'aurais tendance à être d'accord avec sydre
Quoique je rajouterais un facteur (n-2)/(n-1)

#14 - 15-11-2014 23:47:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 882
Si je précisais "sauf erreur" c'est que j'avais de sérieux doutes sur les valeurs proposées . Pour une grille de taille 3 je vois mal comment on peut retourner une aiguille de taille supérieure à 2 ( voir message #6 ) .
Vasimolo
#15 - 16-11-2014 09:59:16
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteauu 82
Pour ma part, j'ai trouvé que pour une longueur L de segment, il fallait à peu près un coté C de valeur 2L -(2L)^(1/3).
#16 - 16-11-2014 11:03:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâetau 82
Si on inverse ta relation on obtient tes barres de taille :
1,16 ; 1,76 ; 2,34 ; 2,90 ; 3,45 ; 4,00 ; ...
Que l'on peut comparer aux valeurs que j'ai fourni :
1,00 ; 2,00 ; 2,00 ; 2,82 ; 3,00 ; 4,00 ; ...
L'estimation a l'air assez bonne .
Il me semble important de se mettre d'accord sur les valeurs exactes de la barre pour les premières tailles de la grille si on veut avoir une petite idée pour les suivantes .
Vasimolo
PS : j'ai proposé le problème à plusieurs sites de maths et tout le monde sèche 
PPS : j'ai fouillé un peu sur la toile pour voir si le problème était connu mais je n'ai rien trouvé 
#17 - 16-11-2014 11:46:11
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
Gâetau 82
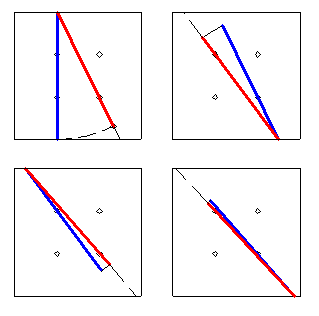
Au risque de me répéter : 3 => 2rac(2)
Même si j'ai eu la flemme de faire le second quart de tour.

#18 - 16-11-2014 12:14:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#19 - 16-11-2014 12:17:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
gâyeau 82
Je dirais que le point crucial est le passage d'un point autour du centre par une extrémité de la barre.
Dans les dimensions impaires, on est donc limité par le passage de la diagonale [(n+1)/2] rac(2)
Dans les dimensions paires, on gagne un cran car on tourne autour du point central sans le franchir:
Pour 4, cela donnerait 3/2 rac(5)
On doit tendre vers un rapport (n+1)/2 rac(2) sinon, on ne franchira pas le point central de la diagonale et on sera borné à un quart de la grille.
En fait, je pense qu'il faut raisonner sur un quart de grille plus éventuellement le carré central.
Je penche pour : 1 / 2 / 2,82 / 3,35 / 4,24 ...
#20 - 16-11-2014 12:24:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
hâteau 82
Je n'ai pas trop le temps de te lire mais je vais y réfléchir ce soir 
gwen27 a écrit:PS ton gâteau précédent, je n'ai même pas compris le problème  et je ne le trouve pas très ludique. et je ne le trouve pas très ludique.
Vasimolo
#21 - 16-11-2014 12:28:57
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
âGteau 82
Bah c'est plus rigolo quand c'est mieux expliqué 
#22 - 16-11-2014 12:33:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâteay 82
C'est évident que je ne suis pas toujours très clair  ( euphémisme ) ( euphémisme )
En tout cas merci de t’intéresser au problème 
Vasimolo
#23 - 16-11-2014 18:25:01
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
gâteai 82
La formule que j'ai sortie est une approximation d'autant plus proche de la réalité qu'on augmente la valeur du segment. Elle est issue de la formule générale qui avait été citée plus haut.
Je ne me suis pas du tout intéressé aux cas particuliers des petits carrés. Et j'ai cherché la taille du coté en fonction de la longueur du segment et non l'inverse.
Vasimolo a écrit:Si on inverse ta relation on obtient tes barres de taille :
1,16 ; 1,76 ; 2,34 ; 2,90 ; 3,45 ; 4,00 ; ...
Que l'on peut comparer aux valeurs que j'ai fourni :
1,00 ; 2,00 ; 2,00 ; 2,82 ; 3,00 ; 4,00 ; ...
L'estimation a l'air assez bonne .
Il me semble important de se mettre d'accord sur les valeurs exactes de la barre pour les premières tailles de la grille si on veut avoir une petite idée pour les suivantes .
Vasimolo
PS : j'ai proposé le problème à plusieurs sites de maths et tout le monde sèche 
PPS : j'ai fouillé un peu sur la toile pour voir si le problème était connu mais je n'ai rien trouvé 
#24 - 16-11-2014 18:28:08
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteu 82
gwen27 a écrit:Je dirais que le point crucial est le passage d'un point autour du centre par une extrémité de la barre.
Dans les dimensions impaires, on est donc limité par le passage de la diagonale [(n+1)/2] rac(2)
Dans les dimensions paires, on gagne un cran car on tourne autour du point central sans le franchir:
Pour 4, cela donnerait 3/2 rac(5)
On doit tendre vers un rapport (n+1)/2 rac(2) sinon, on ne franchira pas le point central de la diagonale et on sera borné à un quart de la grille.
En fait, je pense qu'il faut raisonner sur un quart de grille plus éventuellement le carré central.
Je penche pour : 1 / 2 / 2,82 / 3,35 / 4,24 ...
A mon sens, non, on ne peut pas tendre vers le rapport (n+1)/2 rac2: C'est l'orientation quasi verticale (ou horizontale) qui est la plus contraignante.
#25 - 16-11-2014 18:36:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteeau 82
J'avais bien compris Nodgim 
Chercher une tendance pour les grands carrés n'est certainement pas inutile , on peut aussi chercher les valeurs exactes pour les petits carrés 
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum