|
#26 - 12-11-2014 16:39:19
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
#27 - 12-11-2014 16:42:26
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
Enigmaths 3 QCM 1
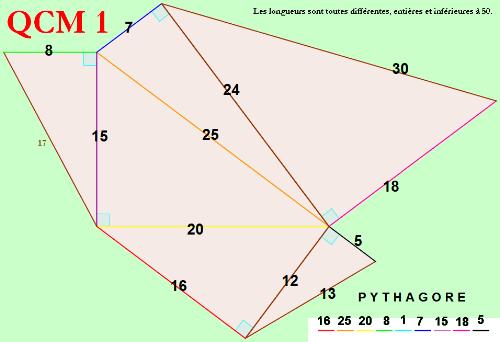
Le A est donné par la longueur des segments marquants les angles droits.
#28 - 12-11-2014 16:43:58
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Enigmaths 3 : QCM
Too late ! 
#29 - 12-11-2014 20:13:51
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Enigmaths 3 QCM 1
Bonjour 
Je voudrais savoir si le dessin est "à l'échelle", c'est-à-dire que si un segment s1 est plus petit qu'un autre segment s2 sur le dessin alors c'est que la valeur entière correspondante à s1 est plus petite que la valeur entière correspondante à s2 ?
Parce que pour l'instant j'ai plusieurs solutions, et je ne vois que le truc expliqué ci-dessus pour déterminer une solution unique.
Il y a sûrement plus simple.
#30 - 12-11-2014 20:29:03
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
enigmaths 3 : qxm 1
Normalement, vous devriez voir le nombre 17 sur l'image. Si vous ne l'avez pas faites F5.
Oui j'avais à l'idée que l'image soit "à l'échelle" (segment plus grand sur l'image est plus grand en réalité) mais comme me l'a fait remarqué gwen, je n'ai nulle part préciser que c'était "à l'échelle" donc le 17 rend la solution unique.q
N'oubliez pas que les longueurs sont toutes différentes et inférieures à 500.
#31 - 12-11-2014 22:26:17
- Puuma
- Habitué de Prise2Tete
- Enigmes résolues : 49
- Messages : 11
enigmatjs 3 : qcm 1
Haha, le segment bleu clair, c'est ce qui symbolise l'angle droit, et qui donne donc l'unité !!
#32 - 12-11-2014 22:39:52
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Enimaths 3 : QCM 1
Oui, j'ai bien vu le 17, mais même avec le 17 j'ai 8 solutions :
Je nommerais les segments comme sur la figure :
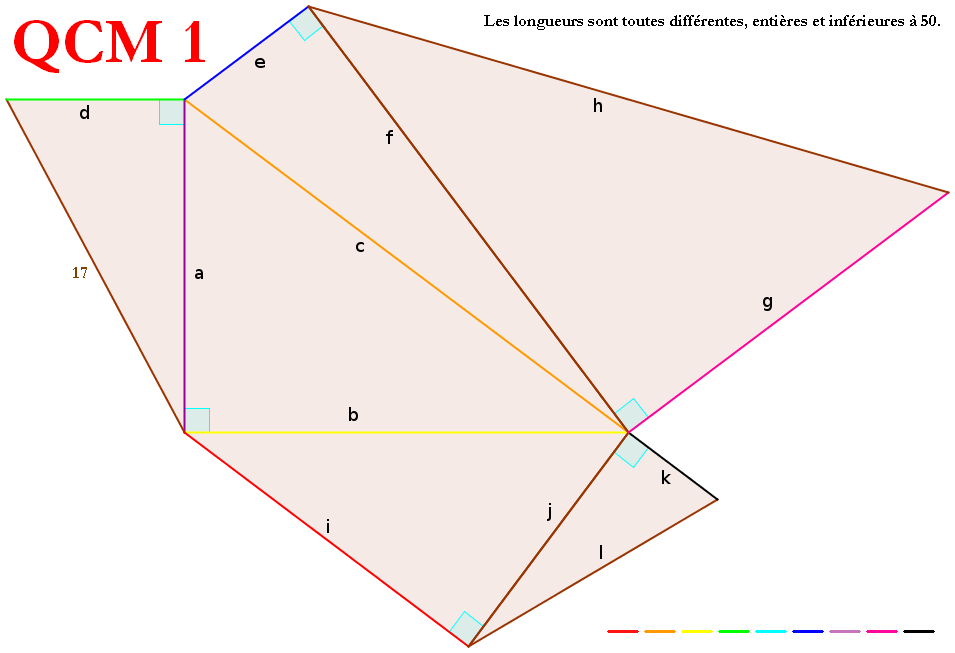
On a donc 6 triangles rectangles dont chacun des trois côtés sont des triplets pythagoriciens. Ces 6 triplets sont :
Tous les triplets pythagoriciens primitifs sont de la forme (p²-q²,2pq,p²+q²) avec :
i) p > q
ii) p et q premiers entre eux
iii) p et q de parité différentes.
Le fait que toutes les valeurs doivent êtres plus petites que 50 implique que l'on doit avoir :
iv) p²+q² < 50
iv) donne p < racine(50) et q < racine(50) autrement dit p et q sont plus petit que 7.
La liste des triplets pythagoriciens primitifs respectant toutes ces conditions est la suivante :
Les autres triplet pythagoriciens ayant leurs valeurs plus petit que 50 sont des multiples de ces triplets là.
Comme 17 est un nombre premier, le triplet (a,d,17) fait forcément partie des triplet primitifs, et parmi ceux-là, il y en a un seul qui se termine par 17 qui est : (15,8,17) donc on a forcément a = 15 et d = 8.
Nos 6 triplets deviennent :
Maintenant nous allons déterminer le triplet (15,b,c) :
Les seuls autres triplets ayant un 15 (qui ne soit pas l’hypoténuse) sont les triplets :
5 * (3,4,5) = (15,20,25)
3 * (5,12,13) = (15,36,39)
Or c ne peut être égal à 39 car 39 est l’hypoténuse de l'unique triplet (15,36,39) alors que c doit être l’hypoténuse des deux triplets (15,b,c) et (f,e,c).
Il ne reste donc plus pour (15,b,c) que le triplet (15,20,25) et donc b = 20 et c = 25.
Nos 6 triplets deviennent donc :
Déterminons maintenant le triplet (f,e,25). Les deux seuls triplets ayant 25 pour hypoténuse sont (15,20,25) et (7,24,25), le premier étant déjà utilisé il ne reste lus pour (f,e,25) que (7,24,25). Ici on a deux choix :
soit (f,e,25) = (7,24,25)
soit (f,e,25) = (24,7,25).
Or f apparaît dans deux triplets qui sont (f,e,25) et (g,f,h), mais 7 n'apparaît que dans le triplet (7,24,25) donc on a forcément (f,e,25) = (24,7,25) et donc f = 7 et e = 24.
Nos 6 triplets deviennent donc :
à partir de là on ne peut plus déterminer algébriquement une solution unique.
Je ne vais pas continuer à tout détailler parce que les raisonnement sont répétitifs, mais les huit solutions que je trouve sont les suivantes :
Solution 1 :
a = 15, b = 20, c = 25, d = 8, e = 7, f = 24,
g = 18, h = 30, i = 16, j = 12, k = 35, l = 37
Ce qui donne les triplets
Solution 2 :
a = 15, b = 20, c = 25, d = 8, e = 7, f = 24,
g = 32, h = 40, i = 16, j = 12, k = 35, l = 37
Ce qui donne les triplets
Solution 3 :
a = 15, b = 20, c = 25, d = 8, e = 7, f = 24,
g = 10, h = 26, i = 16, j = 12, k = 35, l = 37
Ce qui donne les triplets
Solution 4 :
a = 15, b = 20, c = 25, d = 8, e = 7, f = 24,
g = 18, h = 30, i = 16, j = 12, k = 5, l = 13
Ce qui donne les triplets
Solution 5 :
a = 15, b = 20, c = 25, d = 8, e = 7, f = 24,
g = 32, h = 40, i = 16, j = 12, k = 5, l = 13
Ce qui donne les triplets
Solution 6 :
a = 15, b = 20, c = 25, d = 8, e = 7, f = 24,
g = 10, h = 26, i = 16, j = 12, k = 5, l = 13
Ce qui donne les triplets
Solution 7 :
a = 15, b = 20, c = 25, d = 8, e = 7, f = 24,
g = 32, h = 40, i = 12, j = 16, k = 30, l = 34
Ce qui donne les triplets
Solution 8 :
a = 15, b = 20, c = 25, d = 8, e = 7, f = 24,
g = 10, h = 26, i = 12, j = 16, k = 30, l = 34
Ce qui donne les triplets
La figure suggérant k < j laisserait les solutions 4,5 et 6 avec i = 16, j = 12 , k = 5 et l = 13.
Et la figure suggérant a < g < c ne laisserait que la solution 4 avec g = 18 et h = 30
la solution attendu serait donc : 1625208_715185
En remplaçant par les lettres de même rang dans l'alphabet on obtient :
Pythagore 
et donc la valeur en bleu ciel vaut 1 (au départ comme c'était la couleur des angles droit, je pensais que c'était 90).
Il y a sûrement plus simple.
#33 - 12-11-2014 22:56:44
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Enigmaths 3 : QC 1
Ca fait un moment que je ne me frottais pas à une énigme et celle ci est sympathique.
Bon avec un petit excel et un peu de logique visuelle quand il peut y avoir plusieurs réponses on trouve les longueurs qui correspondent aux lettres de l'alphabet en donnant par la suite PYTHAGORE.
Allons voir la suite...
#34 - 12-11-2014 23:13:37
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Enigmaaths 3 : QCM 1
Il fallait que je prenne un peu de temps pour ouvrir Paint et faire les mesures ! 
Merci Pythagore et Saban ! 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#35 - 13-11-2014 10:26:16
- babah
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 6
#36 - 13-11-2014 10:34:50
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Enigmaths 3: QCM 1
Il faut retrouver les triplets pythagoriciens. Merci Wiki pour ceux dits "primitifs" :
(3, 4, 5) (5, 12, 13) (8, 15, 17) (7, 24, 25) (20, 21, 29) (12, 35, 37) (9, 40, 41),
auxquels il faut ajouter leurs multiples :
(6, 8, 10) (9, 12, 15) (12, 16, 20) (15, 20, 25) etc ...
En associant les valeurs aux couleurs, on obtient :
16 25 20 8 ? 7 15 35 5
(Mais pourquoi avoir donner la valeur 17  ? Je ne l'avais pas vue au départ et je n'en ai donc pas eu besoin ? Je ne l'avais pas vue au départ et je n'en ai donc pas eu besoin  ! il suffisait de partir sur la valeur 25 commune au 2 hypoténuses confondues) ! il suffisait de partir sur la valeur 25 commune au 2 hypoténuses confondues)
ET en remplaçant par l'ordre des lettres :
P Y T H ? 7 O ? E
On devine alors le nom du grand mathématicien PYTHAGORE.
Voici une énigme originale, merci  . .
PS : ne va pas trop vite dans la diffusion de ta série  !!! !!!
Certains d'entre nous ne sont pas disponibles tous les jours (je parle en particulier pour moi  ) )
#37 - 13-11-2014 12:14:56
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Eniggmaths 3 : QCM 1
Salut.
s'il manque un segment il doit mesurer 20 pour construire le triangle isocèle de côtés 20 , 20 & 24 sous réserve que j'ai tout compris dans cette énigme .
car en appliquant la formule de Ptolémée au quadrilatère inscrit de côtés
7 , 15 , 20 & 24 et de diagonales 20 & 25
20 x 25 = 7 x 20 + 15 x 24
500 = 140 + 360
#38 - 13-11-2014 13:33:09
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Enimgaths 3 : QCM 1
Congratulations ! 
Décidément, personne n'aime le 17. (Ah je t'avais bien dit que ça servait à rien de l'ajouter !!!)
#39 - 13-11-2014 23:02:28
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1015
#40 - 14-11-2014 21:04:14
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Enigmmaths 3 : QCM 1
Bon, bah c'est terminé !
Beaucoup de réponses et des bonnes ! Je ne vous ferai pas l'injure de parler de Pythagore.
Alors pour le "concept", c'était juste tout simplement l'explication du titre : QCM pour Quel est Ce Mathématicien ? (je vois certains se dire : "Ah ... Juste ça ?"  ) )
#41 - 15-11-2014 03:37:00
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Enigmaths 3 QCM 1
Ah ... Juste ça ? 
|
 |

 Accueil
Accueil
 Forum
Forum