Ben oui , il y a en une infinité dénombrable pour chaque premier chiffre

Vasimolo

Intuitivement, je dirais que ça suit la fameuse loi de Benford: f = log10 (1+1/d) ... mais l'intuition est souvent dangereuse en maths.

Bonjour,
Existe-t-il une raison mathématique pour que l'on trouve plus de 1 que de 2 que de 3 etc?
Le passage de base 10 en base 9 des 10^n est édifiant...

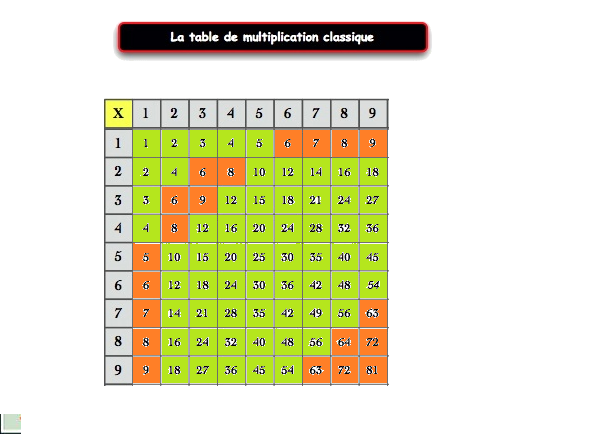
A mon avis, regarder une table de multiplication suffit, même s'il faudrait tenir compte des retenues possibles. si c'est réparti équitablement à un rang, ça ne peut pas l'être. et encore, j'ai laissé un 5 en orange par erreur.

Répartition du 1er chiffre à gauche des puissances des entiers.
L'ensemble des puissances d'un nombre différent de 10 a comme premier chiffre à gauche une valeur variable de 1 à 9 dont on va s'efforcer de mesurer la répartition.

Pour cela, on commence par démontrer que, quel que soit le nombre n et ses puissances, il existe un p tel que n^p=(1+e)*1000...., e aussi petit que l'on veut.

n>1 et il existe n/10^q <1. On pose que n est une borne sup et n/10^q une borne inf. 
On fait le produit des 2 bornes: il est encadré par ses bornes.   
Si le produit >1, on change la borne sup par ce produit. Si le produit <1, on change la borne inf par ce produit.
On refait alors le produit des 2 bornes. 
En renouvelant cette opération autant de fois que nécessaire, on obtiendra ce qu'on voulait: (1+e)*1000...=n^p, e aussi petit que l'on veut.
(En pratique, il faut e < 1/9 pour être sûr d'avoir tous les chiffres représentés au moins une fois. Mais plus e sera petit, plus le décompte sera précis).   

L'utilisation de (1+e)*1000....= n^p à la place de n permet d'ordonner et de grouper les différentes valeurs du 1er chiffre des puissances, ce qui permet leur calcul direct.
1, 1+e, (1+e)², (1+e) ^ 3, ....au lieu de 1,n,n²,...dont le 1er chiffre est aléatoire.

Elle nous permet de tester un échantillon complet ordonné pour les valeurs du 1er chiffre des puissances allant de 1 à 9.
La taille de cet échantillon est telle que (1+e)^p'=10 (on n'arrive pas tout à fait à la valeur exacte 10, mais on peut l'approcher autant qu'on veut).
p' ln(1+e)=ln10
p'=ln10/ln(1+e)
Les valeurs testées entre la puissance 0 de n et la puissance p' de n sont, pour le 1er échantillon:
1,1+e,(1+e)²,....(1+e)^p'
Pour le second échantillon (puissance 1 à p'+1):
n,n(1+e),n(1+e)²....n(1+e)^p'
Pour le 3ème (puissance 2 à p'+2):
n², n²(1+e), n²(1+e)², ...n²(1+e)^p'
Pour le dernier (puissance p-1 à p'+p-1):
n^(p-1), n^(p-1)(1+e), n^(p-1)(1+e²)...n^(p-1)(1+e)^p'.

Dans le 1er échantillon, calculons séparément le nombre de puissances qui commencent par 1, 2 , 3...
(1+e)^p1=2
p1 ln(1+e) = ln2
p1 = ln2/ln(1+e). p1 est le nombre de puissances qui commencent par 1.

Quand on a atteint 2, pour aller jusqu'à 3:
2(1+e)^p2=3
p2=ln(3/2)/ln(1+e)

et ainsi de suite jusqu'à p9.


Si on fait la somme de p1 à p9, par téléscopage, on trouve ln10/ln(1+e)
Si on calcule la valeur de chaque cardinal par rapport au total, on aboutit à un rapport indépendant de 1+e
Pour 1: ln2/ln10
Pour 2: ln(3/2)/ln10
etc...

Cela signifie que, quel soit le nombre n de départ, la répartition sera toujours identique.

Cette répartition suit la loi de Benford, dont on peut rappeler les valeurs approximatives:
pour le 1: 30,10%
pour le 2: 17,61%
pour le 3: 12,49%
pour le 4: 09,69%
pour le 5: 07,92%
pour le 6: 06,69%
pour le 7: 05,79%
pour le 8: 05,12%
pour le 9: 04,58%

Il n'est pas difficile de comprendre que pour les p-1 autres échantillons, on aura la même répartition. La seule différence est qu'on ne démarre plus à 1, mais à un chiffre quelconque, et qu'on termine sur ce chiffre (pour le décompte de ce chiffre, ajouter aux nombres du début ceux de la fin).

J'aurai du mal à te dire si ton raisonnement est juste, mais pour l'instant je n'y vois pas de problème, ta solution est potentiellement juste dans le sens ou elle respecte la loi de Benford dont voici un super article ici

En revanche le seul petit défaut à ta preuve c'est d'avoir utilisé la lettre e, étant donné que ça fait penser à l'exponentielle tout ça tout ça quoi.. voilà c'est tout j'arrête de faire mon casse bonbons

Shadock