|
#26 - 08-01-2015 19:22:47
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,045E+3
Gâtaeu 88
Il n'y a pas trop de solution générale mais la tienne a été démontrée optimale si on a des cercles de rayon 8 dans un carré de 24 pour tenir compte des contraintes de l'énoncé.
http://www2.stetson.edu/~efriedma/cirinsqu/
Après, se pose la question de savoir si le cercle est une forme optimale, vu que des répartitions irrégulières sont parfois plus performantes avec cette forme....
#27 - 08-01-2015 19:27:14
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
GGâteau 88
Ok, c'est une fois de plus bâclé, mais il doit y avoir la place dans ton dessin pour 4 cercles de diamètre (racine (2)- 1). Mieux on peut agrandir en suivant la courbe des cercles distants (croix faite d'arcs de cercle)...
Beh non en fait !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#28 - 08-01-2015 19:45:58
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 888
J'aime bien le dessin de Gwen, j'avais fait le même à peu de chose près ^^
#29 - 08-01-2015 22:41:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#30 - 09-01-2015 15:25:29
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâteeau 88
On voit aisément que N , U(N) et V(N) sont disjoints
Je ne comprends pas pourquoi. Tu pars du principe que N a quelle forme et quelle taille ?
OK, s'il s'agit d'un disque de rayon 2, mais il ne me semble pas qu'on ait prouvé que cette forme était optimale. C'est certes tentant...
Quoi qu'il en soit, chapeau de trouver encore et encore des problèmes aussi intéressants ! 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#31 - 09-01-2015 18:16:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtaeu 88
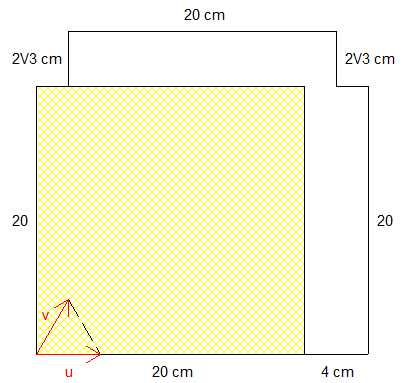
Le fait que N , U(N) et V(N) sont disjoints ne dépend pas de la forme du coulis .
On va essayer de l'expliquer sans Latex :
On a ||u||=||v||=||u-v||=4 .
Si x € N et x € U(N) alors il existe y € N tel que x=U(y) , alors d(x,y)=4 .
Si x € N et x € V(N) alors il existe y € N tel que x=V(y) , alors d(x,y)=4 .
Si x € U(N) et x € V(N) alors il existe y € N et z € N tels que x=U(y)=V(z) , alors z=V^-1 o U(y) donc d(y,z)=4 .
C'est donc impossible dans les trois cas .
Vasimolo
#32 - 09-01-2015 19:34:56
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
gâtezu 88
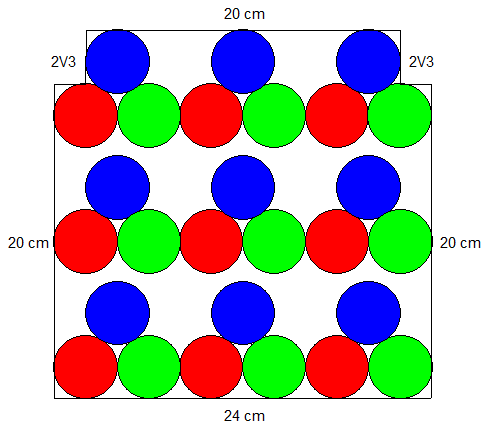
Vasimolo, je ne sais pas si on se comprend bien, mais ton dessin ne correspond pas du tout à ce que j'ai décrit. Je ne comprends pas les ronds de 3 couleurs différentes, et encore moins le calcul associé. Mon nappage correspond à une grosse tàche centrale unitaire de forme presque carrée. Toutes les autres tàches sont très petites et sur le pourtour.
#33 - 09-01-2015 19:39:44
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
gâtzau 88
Il semble en effet que seul Vasimolo comprenne ses propres énigmes 
#34 - 09-01-2015 19:41:20
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 888
Hummm, j'avoue que j'ai du mal à comprendre les explication de nodgim moi aussi.
Nodgim, tu pourrais faire un dessin de quelque chose d'approchant ?
(Mieux que des mots : Une démo !) 
#35 - 09-01-2015 19:42:28
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,045E+3
Gâteua 88
DANS ta grosse tache unitaire, aucun des points de la tache n'est distant de 4 cm d'un autre ?
Parce que sinon, la tache n'a pas plus que la superficie d'un cercle de rayon 2
#36 - 09-01-2015 20:07:26
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâteau 888
La grosse tache carrée au centre s'arrête à un peu plus de 4 cm du bord. Elle a donc une superficie de (20-2*4)²=12²=144. Comparée au 20²=400, Elle occupe donc 144/400=36% de la superficie totale. Ensuite, rien de plus facile que de mettre 16 petites tàches sur le pourtour.
N'est ce pas clair ?
#37 - 09-01-2015 20:09:59
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,045E+3
Gâtea 88
Non, car DANS ta tache il y a des points distants de 4 cm entre eux, et c'est interdit par l'énoncé (une fois qu'on le comprend  ) )
#38 - 09-01-2015 20:15:07
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,045E+3
Gâtaeu 88
OK ! Tu assimile ta tache à 1 points , Vasimolo l'assimile à un ensemble de points.
#39 - 09-01-2015 20:17:27
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
hâteau 88
Mais pourquoi veux tu éclater ma grosse tàche carrée ? Ma grosse tàche carrée est du coulis, c'est une tàche. ça fait quand même un moment que je demande de clarifier les contraintes, on a assez dit qu'on était libre sur la taille et la forme des taches. Alors je choisis un grosse tache carrée au centre.
#40 - 09-01-2015 20:19:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
gâtezu 88
OK je viens de comprendre.
#41 - 09-01-2015 20:28:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#42 - 09-01-2015 20:38:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâeau 88
A la lecture des derniers messages , je comprends enfin le malentendu de départ : une tache n'est pas un point . Je l'ai signalé tardivement car pour moi c'était une évidence 
Vasimolo
#43 - 10-01-2015 10:23:20
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
hâteau 88
C'est bien moi même qui ai fait une mauvaise lecture de l'énoncé, Vasimolo n'y est pour rien.
Maintenant que c'est rentré dans l'ordre, on peut tout de même avancer une règle pour une surface infinie. Tout d'abord, il est curieux de remarquer qu'il suffit d'énoncer qu'aux extrémités d'un segment de longueur donnée, on ne doit pas trouver 2 points rouges pour calculer un recouvrement de rouge indépendant de cette longueur: Le disque de diamètre cette longueur est forcément la forme optimale pour une tache. Ensuite, le placement des taches en nid d'abeille est optimal. De là, on peut calculer facilement le recouvrement max d'une surface infinie: Pi/(8rac3)=0.2267....
Le 0.28 est donc nettement mieux que cette limite, c'est sans doute dû à la possibilité de placer des ronds entiers dans les coins, ce qui est impossible avec la structure nid d'abeille, le rapport entre largeur et hauteur n'étant pas rationnel. On peut sans doute améliorer le rendement nid d'abeille en plaçant le carré en travers de la façon la plus judicieuse possible, mais ce n'est pas sûr qu'on arrivera au 0,28. Avis aux amateurs.
Comme l'a fait remarquer Gwen, le placement en carrés perd de son intérêt pour des surfaces plus grandes: le recouvrement vaut Pi/16 soit 0.1963...
#44 - 10-01-2015 11:41:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gteau 88
nodgim a écrit:Tout d'abord, il est curieux de remarquer qu'il suffit d'énoncer qu'aux extrémités d'un segment de longueur donnée, on ne doit pas trouver 2 points rouges pour calculer un recouvrement de rouge indépendant de cette longueur: Le disque de diamètre cette longueur est forcément la forme optimale pour une tache.
Pour une tache c'est évident mais il y interaction entre les taches . Par exemple dans un carré de côté 4+2R(2) est-on assuré que le meilleur coulis est constitué de deux disques de rayon 2 cm ? Ou même uniquement de morceaux de tels disques ?
Vasimolo
#45 - 10-01-2015 12:02:22
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gtâeau 88
Vasimolo, ma phrase est précédée du contexte de surface infinie (sans bordure).
#46 - 10-01-2015 19:00:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 888
D'accord , mais faire des rapports dans une surface infinie et sans forme n'a pas vraiment de sens 
On peut choisir une forme donnée et observer ce qui se passe quand on l'agrandit à l'infini . La configuration du pâtissier tend vers 19,635..% , la limite avec les translations est 1/3 , entre les deux il y a de la marge .
Il est clair qu'en étendant la taille du gâteau par rapport à celle des taches on estompe les effets de bord mais pourquoi la disposition en nid d'abeille serait-elle la plus performante ?
Ça fait beaucoup de questions sans réponse .
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum