Enigme Gâteau 91 1/3 @ Prise2Tete

Vasimolo · #1

Bonjour à tous

Sa boutique ne désemplit plus depuis qu'il propose ses petits gâteaux carrés , coupés par une diagonale et confectionnés avec des gaufrettes rectangulaires identiques .

Il cache une fève dans l'une des gaufrettes centrales ( coupée par la diagonale ) . Sur l'exemple proposé la chance d'obtenir la fève est la même pour chacune des deux parts ( vert = bleu ) est-ce toujours le cas ?

Bien sûr , le nombre , la taille et la disposition des gaufrettes ne dépend que de la fantaisie du pâtissier

Amusez-vous bien

Vasimolo

Promath- · #2

Quid de la taille de nos gaufrettes?

Vasimolo · #3

Les gaufrettes sont rectangulaires et de taille quelconque

Vasimolo

nodgim · #4

Pour un nb et taille de gaufrettes donnés arrangées en carré, le nb de celles ci coupées par la diagonale est invariant. Celles non coupées aussi. Or on peut tjs réarranger les gaufrettes ttes verticales par exemple. Dans ce cas, par symétrie le nb de gaufrettes non coupées est égal de part et d'autre. Leur surface aussi. Du coup, la surface des coupées est aussi égalisée de part et d'autre. Et donc, c'est la même chose pour n'importe quel arrangement.

Vasimolo · #5

Quelques affirmations mériteraient d'être détaillées , Nodgim

1°) Le nombre de rectangles coupés par la diagonale est invariant ?

2°) Il y a autant de gaufrettes non coupées de chaque côté de la diagonale ?

Il est clair que ces deux résultats permettent de conclure .

Vasimolo

nodgim · #6

Non, le nb de gaufrettes coupées par la diagonale n'est pas forcément invariant. C'est vrai seulement si la coupe traverse 2 bords parallèles, mais ce n'est pas forcément tjs vrai, la coupe peut traverser dans un angle.

Vasimolo · #7

Tu as un exemple où la diagonale traverse un nombre différent de gaufrettes pour deux dispositions des même gaufrettes dans le même gâteau ?

Vasimolo

kossi_tg · #8

Soient respectivement L et l les longueurs et largueurs des gaufrettes. Pour pouvoir faire des bateaux carrés, L doit une multiple de l donc: L=n*l ; n entier non nul.
Par ailleurs le côté noté C des gâteaux carrés est une multiple de L: C=x*L ; x entier non nul. Soit Gx le nom d'un tel gâteau qui contient x*x*n gaufrettes.

Dx=racine(2)*x*L=racine(2)*n*x*l où Dx est la longueur d'une diagonale Gx.

Le plus petit gâteau est constitué de n gaufrettes, c'est le gâteau G1 et D1=racine(2)*L.

Dx/D1=x, il y a donc x gâteaux de même dimension que G1 traversés par une diagonale or dans un G1 toutes les gaufrettes sont traversées les diagonales donc il y a x*n gaufrettes coupées par la diagonale quelle que soit la disposition.

Il y a (x*x*n-x*n)=n*x*(x-1) gaufrettes non traversées soit, par symétrique introduite par la diagonale, 0.5*n*x*(x-1) de chaque côté de la diagonale. Remarquons que x*(x-1) est pair.

I y a au tant de gaufrettes non coupées de chaque côté de la diagonale. A part ces dernières, il reste donc la même surface de gâteau couverte par des gaufrettes coupées des 2 côtés de la diagonales ==> CQFD

nodgim · #9

En fait, il me manque une preuve sous jacente, bien plus compliquée à montrer:
On ne peut poser les gaufrettes dans le désordre (des gaufrettes posées verticalement et horizontalement) qui si le produit Hauteur/ Largeur d'une gaufrette divise le coté du carré (ici dans ton dessin 3*1=3 et coté carré=6).
par au moins 2.
J'ai une autre démo pour ce problème, mais elle fait aussi appel à cette preuve manquante.

Vasimolo · #10

@Kossi : il n'y a aucune raison que L soit multiple de l . On peut tout à fait réaliser le pavage d'un carré 6X6 avec des gaufrettes 3X2 .

@Nodgim : le côté du carré est toujours un multiple du produit de la longueur par la largeur de la gaufrette ( le rapport entre les deux est le nombre de gaufrettes utilisées ) .

Vasimolo

nodgim · #11

Pas tout à fait Vasimolo. Pour un (2,4) un coté 4 suffit. Le coté est un multiple du ppcm. Mais là n'est pas tout à fait la question.

Vasimolo · #12

Oui c'est vrai , c'est l'aire du carré qui est multiple du produit des côtés de la gaufrette .

Vasimolo

titoufred · #13

J'ai une démonstration quand la longueur de la gaufrette est un multiple de la largeur.

On prend alors comme unité de mesure la largeur de la gaufrette, b la longueur entière de la gaufrette, et c = kxb le côté entier du carré, qui est un multiple de b (voir gâteau 80 pour les justifications).

On fait alors un quadrillage du carré et l'on colorie en noir les cases de certaines diagonales, séparées de b cases. Sur l'exemple que tu donnes avec b=3 et c=6 ça donne :

100100
010010
001001
100100
010010
001001

où les 1 sont les cases noires et 0 les cases blanches.

Chaque gaufrette occupe exactement 1 case noire, donc par symétrie, on voit facilement qu'il y a autant de gaufrettes ne touchant pas la diagonale principale au-dessus celle-ci qu'en dessous.
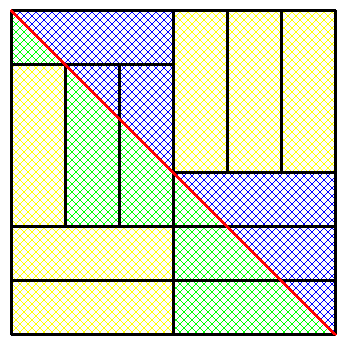
Ceci implique que la surface bleue vaut la surface verte.

Je sèche encore pour le cas général. Tu donnes un peu de temps ?

Vasimolo · #14

A la demande de Titoufred , j'ajoute un peu de temps

On peut estimer que je suis un peu avare en indices ( j'ai une solution ) , mais j'aimerais bien voir d'autres façons d'aborder le problème .

Vasimolo

gwen27 · #15

J'ai du mal à mettre ça en forme, mais je crois tenir une piste.

En passant cette diagonale, on passe d'un coin inférieur gauche à un coin supérieur droit.

J'ai du mal à expliquer pourquoi il y en a autant de l'un en bas que de l'autre en haut.
Ca reste encore trop intuitif... enfin non, mais je n'ai pas le truc """simple et bluffant" qui permette de le prouver.

Si j'arrive à l'expliquer, les formes coupées, en retirent un de chaque côté , donc ça prouverait que le nombre de rectangles entiers de part et d'autre sont égaux.

gwen27 · #16

Bon, je vais essayer de faire simple...

Il y a 5 types de rectangles déterminés par un coin inférieur gauche et un coin supérieur droit. Il y a autant de CIG et de CSD que de rectangles.

Code:

Le coin inférieur gauche est en bas, 
le coin superieur droit est sur la diagonale.

Le coin inférieur gauche est sur la diagonale, 
le coin superieur droit est en haut.

Ces deux cas incrémentent à la fois l'un et l'autre des compteurs suivants, mais bon, on doit pouvoir faire plus clair....

Code:

1 Le coin inférieur gauche est en bas,  
  le coin superieur droit est en bas.

2 Le coin inférieur gauche est en bas,  
  le coin superieur droit est en haut.

3 Le coin inférieur gauche est en haut, 
  le coin superieur droit est en haut.

La coupure par une diagonale implique que le cas 2 est équilibré.
Il reste donc 1 et 3 qui correspondent aux rectangles inscrits entièrement dans une moitié.

Il y a donc autant de rectangles complets en bas qu'en haut, la diagonale ne peut couper que la moitié de la surface restante.

Mais bon, les noeuds "sur la diagonale" me posent un souci de rédaction car ils ont beau être de même nombre, ils ne sont pas pour autant identiques entre eux, n'empêche que l'un incrémente à la fois les CSD du bas et les CIG du haut donc dans ma tête c'est clair car la seconde balise code est vérifiée.

Vasimolo · #17

@Titou : c'est bon pour le cas où la longueur est un multiple de la largeur
@Gwen : ça semble être une bonne piste mais ça reste "un peu" confus

Bonne recherche !!!

Vasimolo

gwen27 · #18

J'ai édité entre temps. On peut faire plus clair, mais ça me semble imparable si on cherche à comprendre mon charabia.

Vasimolo · #19

@Gwen : pour moi ça reste un peu compliqué et pas vraiment clair , la fatigue sûrement

Vasimolo

gwen27 · #20

S'il y a n rectangles, il y a n points B et n points H

B = inférieurs à gauche et H= supérieurs à droite. Ces points peuvent être confondus... (B=H )

Pour un rectangle on a 3 cas :
B et H en bas (sous ou sur la diagonale tous les deux )
B et H en haut (desus ou sur la diagonale tous les deux )
B strictement en bas et H strictement en haut Ce sont les cas où la diagonale coupe le rectangle en deux parties (non nulles) .

Les cas où le rectangle est entier sous la diagonale sont donc égaux aux cas où il est entier au dessus

Vasimolo · #21

Bon j'ai compris l'idée mais il me semble qu'il y a quand même un hiatus dans la démonstration .

Les rectangles de type 2 ne sont pas coupés en deux parts égales par la diagonale . Il pourrait se créer tout le long de la diagonale un déficit d'un côté équivalent à la surface d'une gaufrette . Il y aurait alors une gaufrette de plus d'un côté que de l'autre .

J'ai manqué quelque chose ?

Vasimolo

Vasimolo · #22

Une petite illustration qui montre que la forme carré du gâteau est nécessaire .

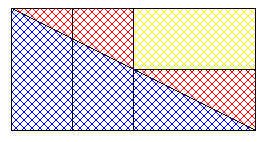
Vasimolo

Franky1103 · #23

J'ai la conviction que, même avec un gâteau carré, ça ne marche pas. Dans ce cas, je dois indiquer un contrexemple ... que je ne trouve pas

Vasimolo · #24

Les avis sont partagés Franky

Je ne donnerai pas le mien ( pour l'instant ) .

Vasimolo

dylasse · #25

Soit c la longueur du coté du gâteau et a et b les longueurs et largeurs des gaufrettes (a>=b).
n est le nombre de gaufrettes (nab=c²)

1. Dans le cas où b=1, montrons que a est diviseur de c.

On va remplir chaque case du gâteau par des chiffres de 1 à a, en commençant par des 1 sur la diagonal, puis des 2 sur la ligne oblique au dessus de la diagonale, puis des 3, etc, jusqu’à a et en recommence avec 1,2, etc et on fait la même chose sur la partie inférieure dans le sens décroissant (exemple avec c=10 et a=4).

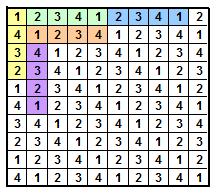
On remarque que chaque gaufrette recouvre exactement a cases, toutes avec a nombres différents.
Calculons N1, le nombre de cases marquées du nombre 1.

soit c=aq+r (où q et r sont les quotients et restes de la division euclidienne de c par a).
N1=c + 2 somme(c – ia) où i varie de 1 à q
N1=c + 2 qc – 2a(q+1)q/2
N1=r + q(c+r)

Pour avoir un recouvrement complet, il faut que N1=n, on calcule c²-N1 a = (a-r)r

Donc un recouvrement total n’est possible que si r=0, c’est à dire a divise c.
Si a divise c, un pavage horizontal est évidemment possible donc a divise c est nécessaire et suffisant pour avoir un recouvrement complet.

2. Toujours lorsque b=1, montrons que les c gaufrettes recouvrant la diagonale occupent la même surface de part et d’autre de la diagonale.
Il y a autant de 1 au dessus de la diagonale qu’en dessous, donc autant de gaufrette au dessus qu’en dessous de la diagonale, qui remplissent une même aire (c²-ac)/2. Comme la diagonale coupe également le gâteau en 2 surface2 égale 2, Les c gaufrettes qui coupent la diagonale occupent une surface identique de part et d’autre de la diagonale.

3. Dans le cas où b est quelconque, on montre également que b est diviseur de c. On se ramène à a et b premiers entre eux (sinon on peut faire un changement d’unité pour avoir B=1).

4. Il nous reste à étudier le cas a et b premiers entre eux.
Une piste :
En découpant toutes les gaufrettes dans le sens de la longueur, on crée un pavage de gaufrette de largeur 1. A ce pavage, on applique le résultat 2.
On ne peux pas conclure à ce stade car certaines gaufrettes placées sur la diagonale initialement (=avant redécoupage) ont été découpées en au moins une gaufrette sur la diagonale mais on ne peut a priori rien dire les b-1 autres…

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 25-01-2015 19:02:00

gâteay 91

#0 Pub

#2 - 25-01-2015 19:32:42

gâtrau 91

#3 - 25-01-2015 21:33:15

Gâtaeu 91

#4 - 26-01-2015 11:44:08

gâteai 91

#5 - 26-01-2015 17:49:54

GGâteau 91

#6 - 27-01-2015 09:23:40

gâteai 91

#7 - 27-01-2015 17:39:41

âGteau 91

#8 - 27-01-2015 21:38:53

gâteay 91

#9 - 28-01-2015 09:03:37

gâteay 91

#10 - 28-01-2015 10:13:49

Gâteu 91

#11 - 28-01-2015 11:42:57

âGteau 91

#12 - 28-01-2015 12:02:50

Gâtea 91

#13 - 28-01-2015 12:42:09

Gâtteau 91

#14 - 28-01-2015 13:42:11

gâyeau 91

#15 - 28-01-2015 21:31:54

Gâteeau 91

#16 - 28-01-2015 22:30:06

fâteau 91

Code:

Code:

#17 - 28-01-2015 22:41:15

Gâteau 1

#18 - 28-01-2015 22:44:21

GGâteau 91

#19 - 28-01-2015 22:57:30

Gâteau 1

#20 - 28-01-2015 23:32:13

gâreau 91

#21 - 29-01-2015 17:26:15

Gâtea u91

#22 - 29-01-2015 22:48:49

Gâtea u91

#23 - 29-01-2015 23:19:39

Gâtaeu 91

#24 - 30-01-2015 00:04:09

Gtâeau 91

#25 - 30-01-2015 18:16:47

Gâteu 91

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums