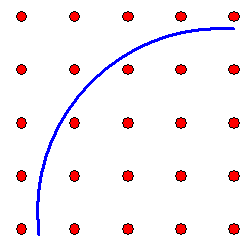
Plaçons le centre du cercle de rayon 30 au centre du repère orthonormé.
Un quart du cercle est décrit par y=g(x)=racine (900 - x^2 )

Notons f(x)=g(x) - ent (g(x))

En calculant f(x) pour x=0, 1, ...30   on remarque:
f(0)=0
f(7)=0.172..
f(20)=0.361...
f(14)=0.533...
f(4)=0.732...
f(11)=0.911...

qui décrit  +/- 0.1 toutes les valeurs entre 0 et 1

Toute grille sera donc touchée par au moins un de ces 6 points et  le pâtissier ne prend donc pas trop de risques...


Alert : je suis n ai pas considéré les décalages horizontaux. On peut les intégrer avec la méthode .indications à suivre


edit

Ainsi on a montré que si la grille passe par une abscisse nulle alors tout cercle touche.

Idée de la démonstration générale que j'essaierais d'écrire correctement ultérieurement si j'y suis encouragé...

Soit un cercle qui maintenant peut aussi être décalé horizontalement.
Considérons des décalages progressifs de 0.14 vers la gauche
Avec le formalisme précédent on a

f(x)=racine (900 - (x - k*0.14 ) ^2  - ent (racine (900 - (x - k*0.14 ) ^2 )

Pour chacun des décalages avec k=0, 1, 2, ..7   , on calcule f(x) pour x=0,1,2...30

On ordonne les résultat à k donné afin de connaitre le maximum de différence. Il est inférieur à 0.7 pour chacun (espérons)

On construit alors des "bulles d'exclusion" de rayon racine( 2*0.07^2 )<0.1

Et on est ramené au cas précédent à montrer qu'il y a forcement un point du repère dans les bulles

Est ce l'idée ?
Cette méthode est un peu lourde car nécessite l'emploi d'un tableur pour que les calculs montrent bien le résultat.

@Portugal : c'est sûr que ta méthode va finir par donner le résultat mais c'est un peu laborieux . Personnellement je n'ai sorti la calculatrice que pour extraire une unique racine carrée
@Enigmatus : tu as raison pour le résultat mais le but est de trouver une méthode permettant de conclure sans utiliser un nuage de point avec un tableur . Pour répondre à la fin de ton message la recherche de ce minimum risque d'être le prolongement naturel du problème .

Pour tous : on peut faire sans artillerie lourde et avec des connaissances de niveau seconde ( voit-on encore l'équation du cercle en seconde ? ) .

Il faut quand même un peu de calcul : je n'ai pas trouvé d'astuce qui tue l'exercice en une phrase .

Bon courage

Vasimolo

Salut Vasimolo,
ça ne passe pas.
Regardons en haut et en bas du cercle: il faut au moins passer la 1ère ligne horizontale de pts. La pente du cercle au franchissement de cette ligne doit être supérieure à la pente min imposée par l'espace entre 2 pts, pente modélisée par un triangle rectangle d'hypothénuse 5 et de petit coté 1, et donc de grand coté V24. Le cos vaut V24/5, son carré 1-1/25=1-12/300.
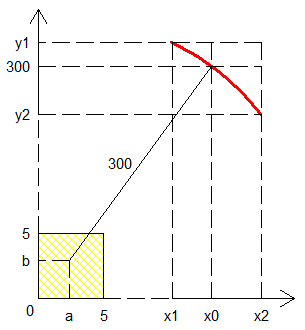
Pour que le cercle passe et en haut et en bas, on vérifie que ça passe quand le pt haut du cercle est à une hauteur à mi-distance entre la ligne immédiatement au dessus et celle immédiatement en dessous (300 est un multiple de 1,donc le pt bas du cercle se trouve aussi au milieu de son interligne). Dans ce cas, on a un triangle rectangle d'hypothénuse 300 et de grand coté 295, donc de cos 295/300=1-5/300 et donc de cos²=(1-5/300)²>1-10/300.

1-10/300 > 1-12/300
Le cos du triangle du cercle est plus grand que le cos du triangle des 2 pts, la pente du cercle est plus petite que la min exigée.

On ne peut pas tracer ce cercle sans toucher les points puisqu'on ne franchit même pas la première ligne de points.

Si le pt le plus haut du cercle est placé à très courte distance au dessus d'un  point du quadrillage, le cercle ne pourra pas franchir la 1ère ligne horizontale de points. Si en revanche il est en dessous et à très courte distance d'un point du quadrillage, il pourra passer la 1ère ligne horizontale de points. Mais c'est le bas du cercle qui ne passera pas.
C'est sur cette idée que j'ai développé mon raisonnement.

Le 300 multiple de 1, c'est un peu le modulo. Si le pt le plus haut du cercle est à x mm au dessus d'une ligne de pts, alors le pt le plus bas du cercle est aussi à x mm au dessus d'une ligne de pts.

Oui. Si ça doit franchir les lignes de pts, ça doit au moins le faire quand le pt du haut du cercle est 5 mm au dessus de sa ligne de pts à franchir, et le pt bas du cercle à 5 mm en dessous de sa ligne de pts à franchir. Si ça ne passe pas quand le cercle est positionné ainsi, ça ne peut pas passer avec un décentrage. Si on décale vers le haut, ça coince en bas, et vice versa.

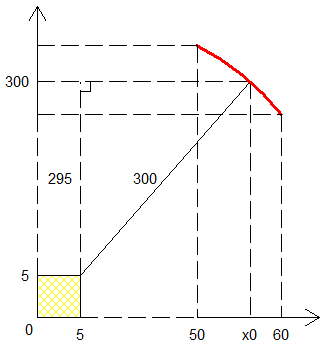
Indépendamment de l'explication que je pourrais donner après, je sais que la pente est variable entre l'entrée du cercle dans la ligne de pts et la sortie de cette ligne de pts. En prenant la sortie, le plus critique, le cos est 294/300=1-6/300. Son carré vaut (1-6/300)² >1-12/300, et ce 1-12/300 est exactement le carré du cos de la pente mini exigée.
J'avais évacué cette possibilité d'emblée en estimant que la variation de pente était négligeable pendant la traversée de la ligne. Calcul fait, ça confirme, mais j'ai eu chaud quand même.

La pente que j'ai calculée ici est égale à l'angle entre la verticale du centre du cercle d'une part, et d'autre part la droite passant par le centre du cercle et le point du cercle situé exactement à hauteur de la 1ère ligne de points franchie.

@Nodgim : je vois un peu mieux de quoi tu parles ( mais je n'ai pas tout compris ) , c'est vraiment très proche de l'idée que j'avais eu .

Le problème est maintenant visible par tous donc chacun peut donner son avis

Bien sûr : immense merci aux participants .

Vasimolo

J'ai la mienne mais j'attends de comprendre celle de Nodgim avant de la donner

Vasimolo

Avec un gâteau plus petit (rayon 5 dm), c'est possible à vue de nez.
Avec un gâteau de rayon 30 dm, cela semble impossible.

Ne serait-il pas intéressant de déterminer la taille maximale pour laquelle le problème a une solution ?
Et la forme de la plage dans laquelle doit se trouver le centre par rapport à la "grille" de points.