|
#1 - 02-08-2015 19:22:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 03-08-2015 08:12:24
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
GGâteau 103
Un gâteau en forme de disque, par exemple, avec des trous pour échapper au maillage ?
#3 - 03-08-2015 09:51:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtea u103
Bien sûr Nodgim avec des trous c'est trop facile 
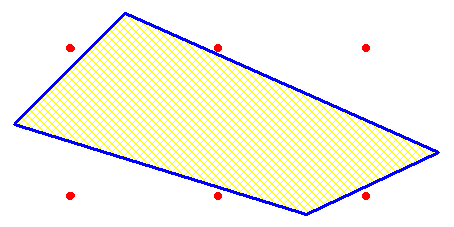
Disons que la base du gâteau est d'un seul tenant et sans trou ( simplement connexe pour les matheux ) .
Vasimolo
#4 - 04-08-2015 18:03:30
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâteau 130
Ah tout de même, je m'en doutais bien, mais je n'ai pas la preuve....
Si le gâteau occupe 5 cases consécutives, c'est la bonne surface mais le périmètre est trop long.
Si le gâteau occupe 4 cases consécutives, c'est le bon périmètre mais pas la bonne surface.
Si le gâteau occupe 1 case, et qu'on prolonge chaque face par une amorce de disque (gâteau en forme de trèfle à 4 feuilles) ça ne va pas non plus.
Si le gâteau occupe 2 ou 3 cases consécutives et qu'on complète la surface manquante par des amorces de disque sur chaque face, ça ne marche pas non plus.
Je n'ai pas même regardé du coté de l' Ellipse, le rapport longueur / largeur est intuitivement bien trop fort.
J'en suis là et je ne vois pas d'autres formes qui seraient meilleures pour le rapport surface/périmètre.
#5 - 04-08-2015 22:38:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
hâteau 103
Le meilleur rapport périmètre/aire est réalisé par les disques , c'est l'inégalité isopérimétrique qui a son rôle à jouer dans l'histoire 
Vasimolo
#6 - 04-08-2015 23:07:18
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâtea u103
Désolé, je ne pense à rien de mieux qu'une sorte de fleur à 4 pétales.
Mais le rapport aire / surface doit valoir 5 cm et le mieux que j'obtienne avoisine 257/62,8 ~ 4,1...
La solution consiste peut-être à déplacer le centre de notre gâteau non pas au centre d'un carré de paillasse, mais au centre d'un côté. On obtiendrait alors quelque chose ressemblant un peu à une paire de...rognons bien écrasés !
Si on part d'un disque de 9 cm de rayon environ et qu'on l'aplatit de façon à ce que ses bords frôlent les points de la paillasse, et qu'on puisse ajouter le complément de gâteau pour la partie symétrique (symétrie par rapport au côté du carré), on obtient une surface de 500 cm2, pour un périmètre qui pourrait avoisiner 100 cm, ce que je ne sais absolument pas démontrer ! Et ce n'est qu'une hypothèse !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#7 - 07-08-2015 01:08:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 1103
Le trèfle de Fix ( le rapport est meilleur que ce qu'il annonce ) .
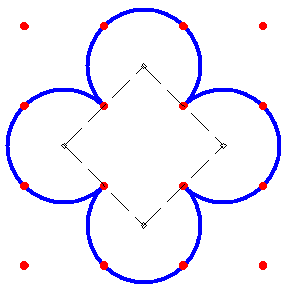
Mais on n'a toujours pas de solution 
Vasimolo
#8 - 07-08-2015 08:43:22
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gteau 103
Le rapport est peut être meilleur mais ce trèfle dépasse 500 cm². Ceci explique sans doute cela.
#9 - 07-08-2015 19:55:37
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâtaeu 103
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#10 - 07-08-2015 23:04:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#11 - 08-08-2015 19:15:37
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
gâteai 103
Bonjour,
En reprenant l'idée du trèfle du message #7, et en plaçant les centres des cercles (qui passent chacun par 2 points rouges de la maille centrale) à une distance d des côtés de la maille centrale (au lieu de 5 cm), j'obtiens ceci :
Cependant, les deux contraintes ne sont pas vérifiées siultanément.
#12 - 08-08-2015 21:14:26
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
gâteai 103
Je ne suis pas convaincu par l'explication de Vasimoolo... Pourrais-tu joindre un schéma?
Un promath- actif dans un forum actif
#13 - 08-08-2015 23:36:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#14 - 09-08-2015 08:11:50
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteeau 103
En partant du trèfle en #7, et en appliquant l'idée de Vasimolo (homothétie ayant pour centre le centre de la maille centrale et de rapport k), on obtient ceci :
Pour info, la transformation ne modifiant les dimensions que dans une seule direction est une affinité.
#15 - 09-08-2015 08:36:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâtau 103
Je ne comprends pas: Vasimolo semblait avoir une solution courte, mais ses derniers messages laissent penser que ce n'est pas tout à fait le cas. Vasimolo, peux tu nous éclairer sur ta position ?
Sinon, une aire max dans un périmètre min, je vois bien ça comme un ballon qu'on gonfle, sauf qu'ici on est en dim 2, mais c'est assez intuitif: ce ballon plat va d'abord recaler son centre dans le carré, puis il va le déborder par les 4 cotés. L'image du trèfle est donc sans doute la plus représentative du max recherché. Ensuite, il a été dit et redit que ça ne marchait pas. Qu'est ce qu'on cherche de plus ?
Autre remarque: pour un disque de diamètre d, le rapport aire/périmètre est d/4, pareil pour un carré de coté c: c/4 !
#16 - 09-08-2015 11:04:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtau 103
Qu'est-ce qu'on cherche de plus 
Contrairement à ce que tu affirmes absolument rien n'a été montré jusqu'à présent . Personnellement je n'ai pas tous les éléments de réponse . Je sais prouver que si le gâteau est convexe alors A/P <5 . Cette inégalité est assez surprenante car elle n'est pas homogène dans les unités et c'est bien sûr le quadrillage qui en est responsable . Le quadrillage ne peut gêner que pour des figures assez grandes on peut donc penser que si on a trouvé une figure dont l'aire est supérieure à 500 cm² avec un rapport A/P supérieur à 5 , on doit pouvoir faire aussi bien avec une aire plus petite .
Pour résumer , beaucoup de questions restent ouvertes 
Vasimolo
#17 - 09-08-2015 11:28:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
âGteau 103
enigmatus a écrit:En partant du trèfle en #7, et en appliquant l'idée de Vasimolo (homothétie ayant pour centre le centre de la maille centrale et de rapport k), on obtient ceci :
Pour info, la transformation ne modifiant les dimensions que dans une seule direction est une affinité.
Merci pour l'info sur l'affinité , on apprend à tout âge 
Tu as fait tes calculs avec l'affinité ou l'homothétie ?
Vasimolo
#18 - 09-08-2015 12:36:37
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteau 1103
Vasimolo #17 a écrit:Tu as fait tes calculs avec l'affinité ou l'homothétie ?
Avec l'homothétie, comme je l'ai indiqué.
#19 - 09-08-2015 12:39:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
âteau 103
Donc le calcul avec l'affinité reste à faire 
Vasimolo
#20 - 09-08-2015 14:58:13
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
hâteau 103
Donc le calcul avec l'affinité reste à faire
L'axe invariant ne peut pas être une médiatrice de la maille centrale, car 4 points rouges se retrouveraient dans le gâteau.
En prenant une diagonale de la maille centrale comme axe invariant, sauf erreur de ma part, on a ceci :
Le calcul du périmètre est beaucoup plus délicat (longueur d'arcs d'ellipse). Je me suis inspiré de ceci : http://serge.mehl.free.fr/anx/long_ellipse.html
#21 - 09-08-2015 17:45:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâeau 103
Bon , on est vraiment très loin du compte , l'aire diminue trop vite par rapport au périmètre .
Vasimolo
#22 - 09-08-2015 18:24:09
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâtteau 103
il faut faire attention que dans une homothétie quand le périmètre est divisé par k , l'aire est divisée par k² . Mais on peut tout à fait réduire la figure selon un seul axe en conservant le rapport A/P . Quand l'aire atteint 500 cm² , il suffit de déformer légèrement la frontière en gardant une aire constante pour satisfaire le pâtissier .
Vasimolo
Sauf que l'affinité (écrasement selon un seul axe) ne conserve pas forcément (certainement même rarement) le rapport A/P : il vaut 2,5 cm pour un carré de 10 cm de côté mais 1,666... pour un rectangle de 10 par 5 !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#23 - 09-08-2015 18:51:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gteau 103
C'est bien pour cette raison que j'avais émis de gros doutes sur l'écrasement selon un axe . A dire vrai je ne suis pas sûr qu'on puisse construire un gâteau réalisant les contraintes du pâtissier mais l'existence du trèfle avec A/P>5 me perturbe un peu .
Si on oublie momentanément l'obligation A=500 cm² , quelqu'un voit-il une autre configuration ( pas une simple variation du trèfle ) où le rapport A/P serait supérieur à 5 ?
Sans doute les rognons de Fix 
Vasimolo
#24 - 10-08-2015 09:28:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâteai 103
La nuit porte conseil 
Il y a une solution au problème et c'est le ballon de Nodgim qui m'a mis la puce à l'oreille . Je ne donne pas la solution mais je vous propose d'imaginer la forme que prendrait une boucle de 1 m de longueur si on l'ouvrait au maximum dans notre réseau pointé .
Vasimolo
#25 - 10-08-2015 11:09:29
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Gâteau 10
Un trèfle à quatre feuilles dont chaque pétale aurait une longueur de 100 / 4 = 25cm, inférieure à 3 x 10 = 30cm. Chaque pétale ne toucherait donc pas à priori de points extérieurs.
|
 |

 Accueil
Accueil
 Forum
Forum