Oui , les points sont choisis selon une loi uniforme et indépendamment les uns des autres .

Vasimolo

Bonsoir,
J'ai commencé par faire des simulations (1 000 000 de galettes à chaque fois), et je trouve que la probabilité de perdre la fève dépasse 10.9 %.
Pour 3 points, on calcule une probabilité de 75 %, confirmée par la simulation.
Je continue à réfléchir…

@Gwen : à quel raisonnement "simpliste" fais-tu allusion ?
@Enigmatus : bonne estimation , après il faut justifier
@Mathieu : Je ne suis pas convaincu .

Vasimolo

Chez moi l'épiphanie, c'est ça...



La fève étant au centre, et le centre étant creux, il a donc 100% de chance qu'elle ne soit pas dedans.

On en conclue qu'il se trompe.
C'était facile cette fois...

Soyons sérieux.
Soit un demi-cercle. Dans le cas où l'ensemble des 7 points est situés sur ce demi-cercle, alors la fève n'est pas dans le gâteau. Mais ça ne me donne pas la probabilité, ni même une approximation valable.
Considérer les points de façon individuel et réduire la probabilité à quant à l'appartenance où non à ce demi-cercle me paraît être un raisonnement un peu simple.
Une loi binomiale ferait-elle l'affaire? Pas sur du tout...

Dans le cas où X est la variable aléatoire tel que X associe k points parmi 7 appartenant au même demi-cercle, on a :

P(X=7) = C(7;7) * (1/2)^7 * (1/2)^0 = (1/128)

On cherche la probabilité contraire :

P(X<7) = 1 - (1/128) = 0,99 environ.

Soit 1% de chance que la fève ne soit plus dans le gâteau.
Résultat qui ne me satisfait pas.

J'ai bien une méthode, mais je sais pas si elle est valable.

Si on partage le gâteau en 4 parts 1234:
Il y a 4 moitiés: 12,23,34,41.
Comme les moitiés ont une partie commune, par exemple 2 entre 12 et 23, et que cette partie commune est comptée 2 fois, il faut la déduire:
Résultat : 4[(1/2)^7-(1/4)^7]=0.03 environ.

Si on partage le gâteau en 8 parts, on fait pareil sauf que c'est un peu plus compliqué, car il y a plusieurs niveaux de surcomptage, qu'il faut déduire du niveau précédent.
Je ne donne pas le détail, mais le résultat: 0,054....

Si la méthode est bonne, je donnerais le détail pour les 8 parts, et tenterais le partage en 16 parts.

J'ai 7 points de départ possibles pour ce raisonnement. ==> 7/64

J'aurais peut-être du rajouter "et chaque chance exclut totalement les autres" pour justifier l'addition des 7 cas.

Je reviens avec une méthode différente, moins fausse j'espère

On va diviser le cercle en [latex]2n[/latex] secteurs de tailles égales et y répartir les 7 points. Pour exclure la fève tout les points doivent être du même côté. Parmi les distributions défavorables, il y a [latex]2n[/latex] possibilités pour la position du premier point précédent les 6 autres dans le sens des aiguilles d'une montre.

Soit une probabilité d'exclusion :
[TeX]2n\frac{\binom{n-1}{6}}{\binom{2n}{7}} \
= \frac{7*2n(n-1)...(n-6)}{2n(2n-1)...(2n-6)}[/TeX]
En passant à la limite on trouve une proba de [latex]\frac{7}{2^6} = \frac{7}{64}[/latex] d'exclure la fève.

Alors soit je me suis encore trompé soit le pâtissier est légèrement prétentieux

Oui c'était l'idée

Il faut et il suffit qu'il y existe un point suivie de 6 points sur le même demi cercle dans le sens des aiguilles d'une montre. Soit [latex]\frac{1}{2^6}[/latex] chances pour un point donné.
Ces probabilités sont exclusives donc la probabilité totale est la somme des 7 probabilités, soit [latex]\frac{7}{2^6} = \frac{7}{64}[/latex]

C'est vrai que dit comme ça c'est beaucoup plus simple

S'agit-il de considérer un heptagone régulier, donc une répartition homogène des points assimilée à une moyenne (dont on donnera une approximation par dispersion), et d'approximer une probabilités en soustrayant l'aire du cercle, à l'aire de cette heptagone régulier?
Ce raisonnement me paraît trop simple, encore une fois.

Le problème exige des connaissances pointues en mathématiques?

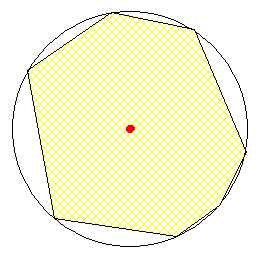
Graphiquement, la fève sera retirée si il existe un demi cercle ne contenant pas de sommets. Il y aura 0 ou 1 sommet situé à l’extrémité gauche de cet éventuel demi cercle

Avec 7 sommets :
Pour un sommet donné, la probabilité qu'il soit situé a l’extrémité gauche du demi cercle est (1/2)^6=1.56%

Comme il y a au plus 1 sommet situé à gauche du vide , la probabilité cumulée est inférieure à 7*1.56=10.9%

Pas tout a fait 10% mais le pâtissier, commerçant, s'octroie le droit d'arrondir les angles…de ses galettes…

___

remarque

Avec 3 sommets, une intégration élémentaire montre que la probabilité est de 3/4 de perdre la fève.

En effet, Si on prend les 2 premiers sommets formant un angle alpha (entre 0 et pi ) alors la probabilité que les 3 incluent la fève est alpha/2pi. (il faut 3 points couvrant plus de pi pour couvrir la fève)

En intégrant la valeur de alpha entre 0 et pi (le problème étant symétrique ) on trouve que le probabilité que la fève soit dans la galette  est de 1/4.

Est ce la bonne voie ou suis a coté de la plaque de cuisson ?