bonjour.

si je prend le plus grand côté sur lequel je place debout 63 rectangles j'obtiens un ratio de 32/33 . je perd donc 1/33 du gâteau .

Vasimolo #22 a écrit:

@Enigmatus : c'est bien ça mais pourquoi est-ce la meilleure solution ?

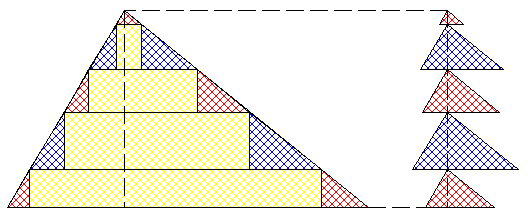
On découpe le triangle initial en n bandes horizontales (y compris le triangle vide tout en haut), de hauteurs h_1, h_2,...,h_n.
H est la hauteur du triangle initial, et S sa surface. On définit les coefficients k_i = h_i / H.
La surface perdue est égale à (somme, pour i=1->n)(S * k_i^2).
On sait que somme(k_i)=1, et on veut minimiser somme(k_i^2). On montre facilement que les k_i doivent être égaux (k_i=1/n, surface perdue=S/n).
On veut que n soit le plus grand possible, donc chaque bande horizontale ne contient qu'une part de gâteau, et n=64.

Il me semble avoir donné une réponse en français ; et je ne comprend pas la réponse donnée ; excuse moi de t'avoir importuné.

Bon impossible pour moi de charger la moindre image depuis mon ordinateur
Pour le moment je trouve qu'un triangle isocèle rectangle est la meilleur des solutions. Partant du fait que les rectangles s'agencent bien dans un grand rectangle, bon il reste un peu de place puisqu'ils ne sont que 63.
Du coup en coupant le grand rectangle en deux de selon une diagonale et en ajoutant une hauteur de rectangle (petit) à la hauteur du triangle qui passe par son sommet droit est suffisant. Mais il y a sans doute mieux.

shadock

Après une nuit de réflexion , la solution est probablement un empilement de 63 rectangles semblables en progression géométrique. Quant à prouver que c'est la solution optimale, il me faudra une autre nuit de réflexion.

Ah oui mais attend 63=9*7 donc ils s'agencent parfaitement dans le grand rectangle

Bon j'essaye de finaliser ma réponse au plus vite du coup

En dernier recours, avant la fin du temps règlementaire, je divise le plus grand côté du triangle en 65 parties égales: les 63 parties centrales forment le petit côté des parts de gâteau toutes perpendiculaires à ce grand côté du triangle, toujours sans prouver un éventuel optimum.

•    Un peu déçu car je cherchais une explication pour laquelle cette forme d’empilement est optimale au delà de l’explication intuitive sur le fait que les parts « verticales » perdent de la place du fait de la séparation du sommet.

•    Pour la somme minimale je vois que je ne suis pas le seul à ne pas avoir écrit une démo digne de ce nom. Je m’y colle :

-    Soit la somme des Ai ^2 avec Ai quelconque.
-    On note M la moyenne arithmétique de Ai, et des Bi tels que Ai = M + Bi
-    On développe Somme [ (M+Bi) ^2 ] = nM + Somme (Bi) ^2 + 0
                 (car somme Bi=0 par construction)
-    Qui est donc minimum pour Bi=0 quel que soit i
-    D’où Ai=M pour tout i