Question supplémentaire :

La plus haute tour du monde mesurera bientôt 1000 mètres de hauteur, pour 250 mètres de largeur.

Saurez-vous estimer la différence de mesure entre le côté de la base, et le côté du sommet de la tour?

Je suppose qu'il s'agit de la verticale, qui diffère au sommet de la base à cause de la rotondité de la terre...

On trouve (approximativemet) une différence de c.h/6 400 000 si h est la hauteur du building et c la longueur du côté de la base données en m

Pour 1000 m de haut et 250m de large, ça donne 25/640=1/25,6 soit autour de 4 cm... rien de méchant !

Bonsoir / Bonjour,

Si les verticales du gratte-ciel sont déterminées au fil à plomb, alors elles ne sont pas parallèles mais présentent un angle d'ouverture (dont le sommet serait le centre de la terre)

C'est ça ?

Bonne nuit !

Peut être que les faces de l'immeuble sont parfaitement à la verticale du lieu ?

Les verticales passent par le centre de la terre.
Elles ne sont pas parallèles d'un endroit de la tour à un autre.
La tour est un tronc de pyramide.

Ou je n'ai rien compris au problème, car rien n'empêche de construire une tour cylindrique à base carrée.

EDIT ça doit faire dans les 4 cm (pi/80 m)

Saurez-vous estimer la différence de mesure entre le côté de la base, et le côté du sommet de la tour?

Grosso modo 40cm erreur de conversion 40mm soit 4 cm

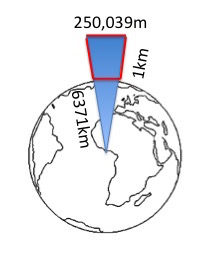
Edit calcul
je néglige la courbure de la terre sur 250m
2 droites parallèles, un triangle -> Thales

(6371+1)/6371*250 = 250,039m

Bonjour

On peut considérer qu'un grand cercle sur la terre fait environ 40 000 km . le côté de la tour fait 1/4 km c'est à dire 1/160 000 du grand cercle . L'angle au centre de la terre qui va capter le côté de la tour vaut a=pi/80 000 ( en radians ) . Cet angle va capter R.a au bas de la tour et (R+1).a au sommet ( R est le rayon de la terre ) . La différence est donc de a km soit environ 4 cm .

Vasimolo

C'est plutôt amusant.
Tout le monde a compris l'évidente raison, mais tout le monde ou presque trouve un résultat différent pour le calcul...

Bonjour

Un petit schéma très exagéré (en rouge le pourtour du building) (r : rayon de la Terre, h : hauteur du building, Lh : largeur en haut et Lb : largeur en bas)



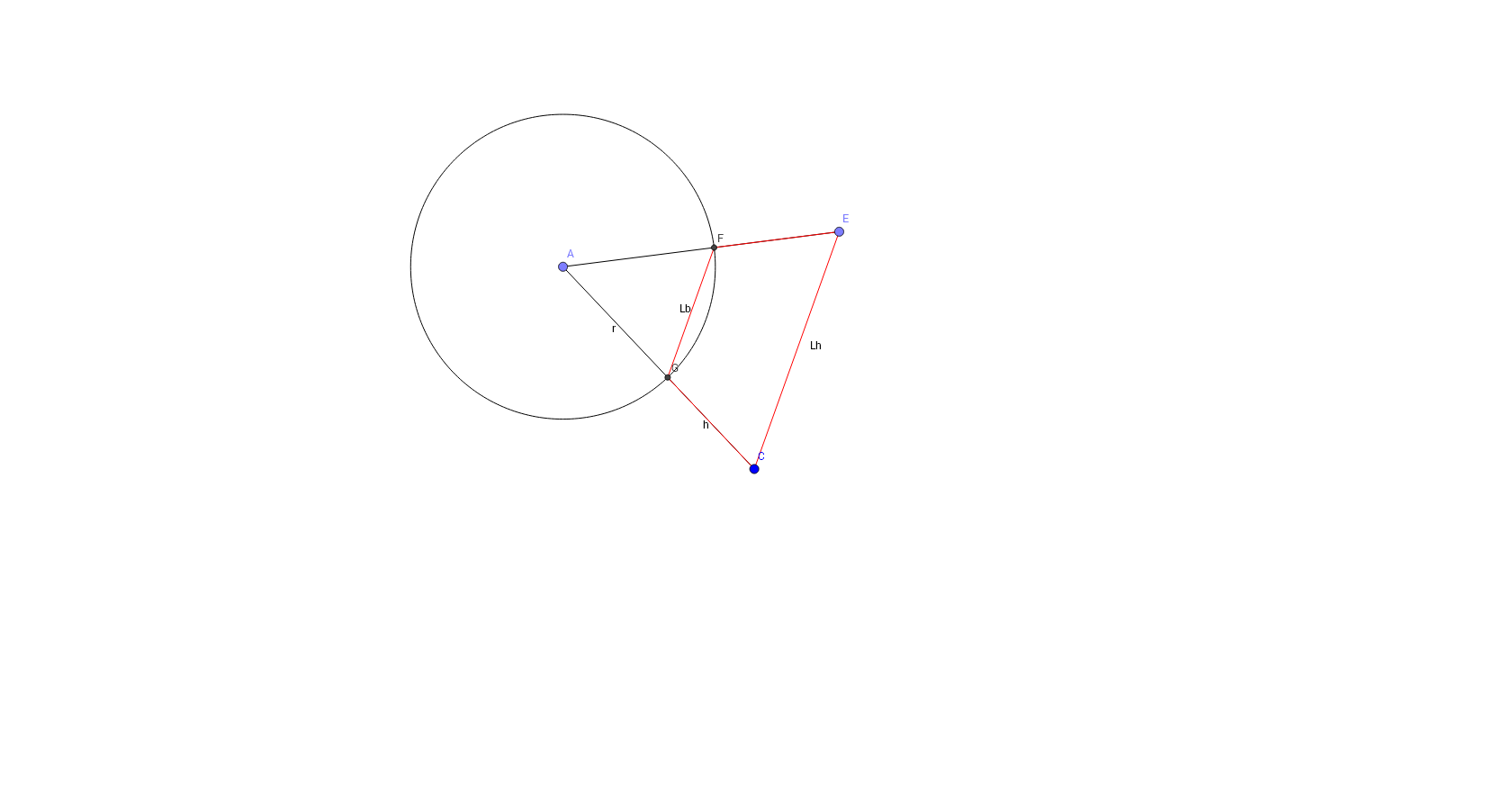
Celui-ci est un trapèze et non un rectangle. On peut discuter sur la façon d'en mesurer la largeur à la base, il y a trois options : celle que j'ai retenue (la corde), la mesure de l'arc de cercle et la mesure du segment tangentiel entre les deux piliers et parallèle à la corde. Ça dépend avec quel instrument on mesure, mais ne changera pas grand chose numériquement.

La hauteur est normalement mesurée sur les piliers. Si on est d'accord sur ces mesures, on a r/Lb = (r+h)/Lh, soit Lh-Lb=h/r.

A cet endroit de la Terre, celle-ci a un rayon proche du rayon équatorial qui vaut 6378,137 km d'après Wikipedia, on a donc une différence de Lh-Lb égale à 0,0157cm.

Largement inférieur aux imprécisions liées à la construction du truc si je ne me suis pas trompé.

PrOliG, je ne comprends pas bien ton calcul. Ton raisonnement est correct, mais ton résultat est faux.

Effectivement, cela donne 4 cm.
Quand m'est venu l'idée de faire ce petit calcul pour la tour en construction, je m'attendais à 1 mm d'écarts dans le pire des cas, ou plus surement non visible à l’œil nu...

Je n'avais pas notion que la courbure de la terre puisse impacter la structure de plusieurs centimètres, et sur le coup, j'étais assez bluffé (mais je suis peut-être naïf) ...
Enfin, c'est vrai, quoi, 4 cm, c'est deux doigts, ce n'est pas complètement négligeable. Ca se voit clairement à l’œil nu. Pas suffisant pour fragiliser la structure, probablement. Mais avec deux doigts, on en fait des choses, c'est large, on peut les mettre dans plein de trucs (je parlais pas de ça, bande de vicieux).
Enfin, bref, vous m'avez compris, je suis surpris par ce résultat plutôt inattendu pour moi.
Je n'ai aucune notion d'architecture, mais je me demande si ce genre de problème est pris en compte dans les calculs des architectes et des ingénieurs.

Sur la lune, la même tour aurait près de 14 cm d'écart entre la base et le sommet.
Et quand nous serons en mesure de construire des tours sur la lune, on peut imaginer sans peine que la pesanteur étant moindre, et la technologie plus grande, une tour de 10 km de hauteur soit concevable... Farfelu, on est d'accord, mais cela donnerait près de 150 cm d'écart entre la base et le sommet.
Je trouve ça étonnant et plutôt amusant.

Bravo à tous.

De toutes façons, le fait de garder les murs parallèles va dans le bon sens : Les 2 murs penchent alors l'un vers l'autre, lui conférant une structure en pyramide tronquée, plus solide qu'un pavé droit !

golgot59 a écrit:

De toutes façons, le fait de garder les murs parallèles va dans le bon sens : Les 2 murs penchent alors l'un vers l'autre, lui conférant une structure en pyramide tronquée, plus solide qu'un pavé droit !

La pyramide est renversée, les murs auront plutôt tendances à s'écarter.
Mais effectivement, ça ne doit pas impacter grand chose en terme de structure, les tours de ce type sont de toute façon souples, elles peuvent subir des variations de quelques mètres.

J'ai envie d'introduire un effet de relativité générale dans ce problème

Je t'en prie...