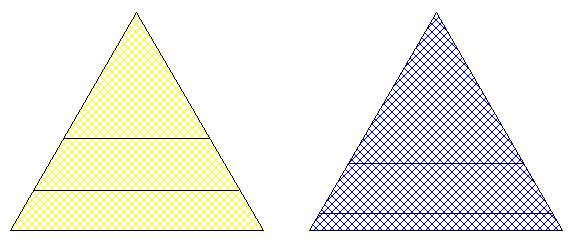
|
#1 - 11-11-2016 18:32:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#2 - 11-11-2016 20:24:21
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
gâtezu 129
J'ai une solution pour n=1 ...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#3 - 11-11-2016 22:24:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtau 129
n=1 , d'accord, mais il va falloir salir un peu le couteau ou dire pourquoi on ne peut pas le salir 
Vasimolo
#4 - 11-11-2016 22:42:45
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gâteaau 129
Bon... Pour la découpe type 1, avec perimetres constants les longueurs de coupe (l1, l2, l3...) sont des fractions de nombres entiers de la forme:
l1= 3^(n-1) / ((3^n -1 )/2), l2=l1+3^(n-2) / ((3^n -1 )/2), l3 = l2+3^(n-3) / ((3^n -1 )/2), etc...
Pour la découpe type 2, avec aires contantes, les longueurs de coupe (l1, l2, l3...) sont des racines carrées de fractions de nombres entiers de la forme:
l1 = sqrt(1/n), sqrt(2/n), sqrt(3/n), sqrt(4/n), etc...
Donc pour qu'il y ait une chance qu'une coupe type 1 soit égale à une coupe type 2, il faut n soit un carré sinon on a un rationnel égal a un irrationnel.
Je n'en ait pas vu pour n=4, 9, 16 ou 25.. et si on va plus loin on a trés vite des fractions de nombres trés grand...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#5 - 11-11-2016 22:53:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtau 129
C'est l'idée Dan , après il faut salir un peu le couteau 
Vasimolo
#6 - 11-11-2016 23:06:21
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gâteau 12
ok.. je viens d'en voir une coupe presque identique...
pour n=27: la 1ere coupe type 1 est de 2541865828329/3812798742493 soit tres legerement au dessus de 2/3, et la 12eme coupe type 2 est de sqrt(4)/sqrt(9) soit 2/3. Voila donc 2 coupes identique à la precision pres du couteau...
Cependant je pense que au sens strict, ce n'est pas possible...
Voici mes resultats jusqu'à 12:
Pour 2 parts avec perimetres constants:
3/4 , soit:
0.750000
Pour 2 parts avec aires constantes:
sqrt(1/2) , soit:
0.707107
Pour 3 parts avec perimetres constants:
9/13 12/13 , soit:
0.692308 0.923077
Pour 3 parts avec aires constantes:
sqrt(1/3) sqrt(2/3) , soit:
0.577350 0.816497
Pour 4 parts avec perimetres constants:
27/40 9/10 39/40 , soit:
0.675000 0.900000 0.975000
Pour 4 parts avec aires constantes:
sqrt(1/4) sqrt(1/2) sqrt(3/4) , soit:
0.500000 0.707107 0.866025
Pour 5 parts avec perimetres constants:
81/121 108/121 117/121 120/121 , soit:
0.669421 0.892562 0.966942 0.991736
Pour 5 parts avec aires constantes:
sqrt(1/5) sqrt(2/5) sqrt(3/5) sqrt(4/5) , soit:
0.447214 0.632456 0.774597 0.894427
Pour 6 parts avec perimetres constants:
243/364 81/91 27/28 90/91 363/364 , soit:
0.667582 0.890110 0.964286 0.989011 0.997253
Pour 6 parts avec aires constantes:
sqrt(1/6) sqrt(1/3) sqrt(1/2) sqrt(2/3) sqrt(5/6) , soit:
0.408248 0.577350 0.707107 0.816497 0.912871
Pour 7 parts avec perimetres constants:
729/1093 972/1093 1053/1093 1080/1093 1089/1093 1092/1093 , soit:
0.666972 0.889296 0.963403 0.988106 0.996340 0.999085
Pour 7 parts avec aires constantes:
sqrt(1/7) sqrt(2/7) sqrt(3/7) sqrt(4/7) sqrt(5/7) sqrt(6/7) , soit:
0.377964 0.534522 0.654654 0.755929 0.845154 0.925820
Pour 8 parts avec perimetres constants:
2187/3280 729/820 3159/3280 81/82 3267/3280 819/820 3279/3280 , soit:
0.666768 0.889024 0.963110 0.987805 0.996037 0.998780 0.999695
Pour 8 parts avec aires constantes:
sqrt(1/8) sqrt(1/4) sqrt(3/8) sqrt(1/2) sqrt(5/8) sqrt(3/4) sqrt(7/8) , soit:
0.353553 0.500000 0.612372 0.707107 0.790569 0.866025 0.935414
Pour 9 parts avec perimetres constants:
6561/9841 8748/9841 729/757 9720/9841 9801/9841 756/757 9837/9841 9840/9841 , soit:
0.666701 0.888934 0.963012 0.987705 0.995935 0.998679 0.999594 0.999898
Pour 9 parts avec aires constantes:
sqrt(1/9) sqrt(2/9) sqrt(1/3) sqrt(4/9) sqrt(5/9) sqrt(2/3) sqrt(7/9) sqrt(8/9) , soit:
0.333333 0.471405 0.577350 0.666667 0.745356 0.816497 0.881917 0.942809
Pour 10 parts avec perimetres constants:
19683/29524 6561/7381 28431/29524 7290/7381 243/244 7371/7381 29511/29524 7380/7381 29523/29524 , soit:
0.666678 0.888904 0.962979 0.987671 0.995902 0.998645 0.999560 0.999865 0.999966
Pour 10 parts avec aires constantes:
sqrt(1/10) sqrt(1/5) sqrt(3/10) sqrt(2/5) sqrt(1/2) sqrt(3/5) sqrt(7/10) sqrt(4/5) sqrt(9/10) , soit:
0.316228 0.447214 0.547723 0.632456 0.707107 0.774597 0.836660 0.894427 0.948683
Pour 11 parts avec perimetres constants:
59049/88573 78732/88573 85293/88573 87480/88573 88209/88573 88452/88573 88533/88573 88560/88573 88569/88573 88572/88573 , soit:
0.666670 0.888894 0.962968 0.987660 0.995890 0.998634 0.999548 0.999853 0.999955 0.999989
Pour 11 parts avec aires constantes:
sqrt(1/11) sqrt(2/11) sqrt(3/11) sqrt(4/11) sqrt(5/11) sqrt(6/11) sqrt(7/11) sqrt(8/11) sqrt(9/11) sqrt(10/11) , soit:
0.301511 0.426401 0.522233 0.603023 0.674200 0.738549 0.797724 0.852803 0.904534 0.953463
Pour 12 parts avec perimetres constants:
177147/265720 59049/66430 19683/20440 6561/6643 264627/265720 729/730 265599/265720 6642/6643 20439/20440 66429/66430 265719/265720 , soit:
0.666668 0.888891 0.962965 0.987656 0.995887 0.998630 0.999545 0.999849 0.999951 0.999985 0.999996
Pour 12 parts avec aires constantes:
sqrt(1/12) sqrt(1/6) sqrt(1/4) sqrt(1/3) sqrt(5/12) sqrt(1/2) sqrt(7/12) sqrt(2/3) sqrt(3/4) sqrt(5/6) sqrt(11/12) , soit:
0.288675 0.408248 0.500000 0.577350 0.645497 0.707107 0.763763 0.816497 0.866025 0.912871 0.957427
[...] je saute a n=28:
Pour 18 parts avec perimetres constants:
129140163/193710244 43046721/48427561 14348907/14900788 47829690/48427561 192913083/193710244 531441/532171 193621671/193710244 48420180/48427561 19683/19684 48426741/48427561 193709151/193710244 532170/532171 193710123/193710244 48427551/48427561 14900787/14900788 48427560/48427561 193710243/193710244 , soit:
0.666667 0.888889 0.962963 0.987654 0.995885 0.998628 0.999543 0.999848 0.999949 0.999983 0.999994 0.999998 0.999999 1.000000 1.000000 1.000000 1.000000
Pour 18 parts avec aires constantes:
sqrt(1/18) sqrt(1/9) sqrt(1/6) sqrt(2/9) sqrt(5/18) sqrt(1/3) sqrt(7/18) sqrt(4/9) sqrt(1/2) sqrt(5/9) sqrt(11/18) sqrt(2/3) sqrt(13/18) sqrt(7/9) sqrt(5/6) sqrt(8/9) sqrt(17/18) , soit:
0.235702 0.333333 0.408248 0.471405 0.527046 0.577350 0.623610 0.666667 0.707107 0.745356 0.781736 0.816497 0.849837 0.881917 0.912871 0.942809 0.971825
et pour n=27, c'est un peu pareil...
On voit que les fractions pour les perimetres identiques ont des nombres (numerateur et denominateur) de plus en plus grand qui ne se simplifient pas (ou pas suffisament (il y a le cas ci-dessus de 729/730)), alors que les fractions pour les aires identiques ont des nombres qui restent tout petit... On aura donc jamais 2 coupes identiques
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#7 - 11-11-2016 23:07:45
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
âGteau 129
au fait quand tu dit "2 coupes identiques" c'est :
- 2 coupes sur chaque gateau (ce qui devient tres improbable..)
ou
- 2 coupes total (une sur chaque gateau) ?
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#8 - 11-11-2016 23:12:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
hâteau 129
Il faut trouver une ligne de coupe identique sur chaque gâteau .
Vasimolo
#9 - 11-11-2016 23:28:04
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
gâtrau 129
Aussi.. il s'agit bien de gateau théorique, car pour la découpe à périmêtre constant, dês que l'on a plus de 7 ou 8 parts, la dernière part est si petite qu'il n'y a plus rien a manger...
En fait si on veut parler de limites...
Quand x tend vers l'infini, on prend n=9*x
la premiere ligne en decoupe par aire est egale a la ligne 4*x de la decoupe par perimetre. Je crois que c'est le mieux que je puisse faire....
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#10 - 12-11-2016 05:17:12
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Gâteeau 129
Salut,
On montre que l'existence de lignes de coupe identiques est équivalente à l'existence d'un triplet (n,ka,kp)∈N3 vérifiant l'équation :
√kan=3−31−kp3−31−n
La ka-ème ligne de coupe (en partant du sommet) sur le gâteau des aires est alors identique à la kp-ème ligne de coupe sur le gâteau des périmètres.
En étudiant le comportement des différents termes on se rends compte assez rapidement qu'il n'existe pas de solution !
#11 - 12-11-2016 10:34:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâreau 129
@Dan : Il faut aller jusqu'au bout même si la fin est purement théorique 
@Sydre : Je ne trouve pas tout à fait les mêmes équations que toi , il me semble qu'il manque un facteur .
Bon courage aux autres .
Vasimolo
#12 - 12-11-2016 11:09:23
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteau 19
Salut Vasimolo.
Je donne ici les résultats des hauteurs hn (prises depuis le sommet du triangle, et donc n croît de haut en bas)) pour le partage en n parts, dans chacun des 2 cas. La hauteur du triangle est supposée égale à 1.
Pour le partage en aire :
Entre 3 traits consécutifs, on a la relation hn² = 2 h(n-1)² - h(n-2)²
Et on arrive à la formule simple, pour tout k compris entre 1 et n : hk = V(k/n)
Pour le partage en périmètre :
Entre 3 traits consécutifs, on a la relation hn= (4/3) h(n-1) - (1/3) h(n-2)
Et on arrive à la formule, pour tout j compris entre 1 et n :
hj = (3^j-1)* 3^(n-j) / (3 ^ n - 1)
Pour un même n, pour avoir au moins une découpe au même endroit, il faudrait :
V(k/n) = (3^j-1) * 3^(n-j) / (3 ^ n - 1) avec 0 < k,j < n.
En mettant au carré et en déplaçant des termes, ça donne :
3^( 2n - 2j) = (k/n) * (3^n-1)²/ (3^j - 1)²
A gauche on a une puissance de 3 (au moins 3²). A droite, il n'y a aucun multiple de 3² disponible, car k/n < 1 et le reste est premier avec 3.
C'est donc impossible d'avoir des découpes confondues.
#13 - 12-11-2016 11:20:30
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Gâtea 129
Bon, commencons:
En supposant le triangle de côté 1, avec n parts
Si on résout pour les aires, on trouve rac(p/n) p allant de 1 à n-1 pour les longueurs des coupes.
Si on résout pour les périmètres, on trouve (3^p-1)C/2*3^p avec C le périmètre de chaque part
En détermine en sachant que pour p = n, on trouve le trait du bas, de longueur 1, donc C = 2*3^n/(3^n-1)
Les longueurs des coupes sont finalement 3^(n-p)*(3^p-1)/(3^n-1) p allant de 1 à n-1.
Il ne reste plus qu'à trouver un n tel qu'il existe p,q < n tels que n3^(2n)/(3^n-1)^2 = q3^(2p)/(3^p-1)^2
Le n est très embêtant car on ne peut pas se ramener à une équation polynomiale...
Edit:
petite simplification, les deux dénominateurs ne sont pas divisibles par 3. pour compenser la mutiplicité du terme de gauche, q doit donc être divisible par 3^2(n-p)
q =q'3^2(n-p) alors le problème devient n/(3^n-1)^2 = q'/(3^p-1)^2
Ca devient plus agréable...
#14 - 12-11-2016 11:28:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâreau 129
@Nodgim : il doit manquer quelques carrés dans ta formule .
@Caduk : tu as presque fini , il n'y a plus qu'à se débarrasser des fractions ...
Vasimolo
#15 - 12-11-2016 12:08:54
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteu 129
Si l'on suppose que le gâteau est de côté 1, les distances entre le sommet du gâteau et les lignes de coupes sont de la forme V3/2.Vk/Vn pour le premier gâteau, et V3/2.(3^k-1)/(3^n-1).3^(n-k) pour le deuxième (où 1<=k<=n-1).
On est donc amené à se demander si, pour une certaine valeur de n, il existe k et k' tels que (3^k-1)/(3^n-1).3^(n-k) = Vk'/Vn.
Or si a et b sont premiers entre eux, la fraction (3^a-1)/(3^b-1) ne se simplifie que par 2, d'où on tire que le dénominateur de la fraction (3^k-1)/(3^n-1).3^(n-k) après simplification vaut au minimum 3^(n/2)+1, ce qui est bien trop grand pour être égal au dénominateur de Vk'/Vn après simplification.
#16 - 12-11-2016 12:17:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 1229
@Ebichu :3a−13b−1 ne se simplifie que par 2 : tu as une justification ?
Vasimolo
#17 - 12-11-2016 12:54:19
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 219
En supposant a<b, ça fait 1+3+32+...+3a−11+3+32+...+3b−1 après simplification par 2, et donc 1+3+...+3a−11+3+...+3a−1+3a.[1+3+...+3b−a−1].
S'il y a un facteur commun au numérateur et au dénominateur, c'est donc un facteur commun à (1+3+...+3a−1) et 3a.[1+3+...+3b−a−1], donc un facteur commun à 3a−12 et à 3b−a−12.
Ce qui est valable pour a et b est valable pour a et (b-a). On conclut en utilisant que PGCD(a;b)=1.
#18 - 12-11-2016 13:07:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 1129
Parfait : j'avoue être impressionné par la simplicité de ta solution , bravo !!!
Vasimolo
#19 - 12-11-2016 13:21:10
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gââteau 129
Moi aussi  L'arithmétique est mon point faible, alors quand je trouve un truc c'est la fiesta. L'arithmétique est mon point faible, alors quand je trouve un truc c'est la fiesta.
Et comme je disais à nodgim l'autre jour, merci pour tes énigmes. Tes gâteaux son toujours aussi appétissants !
#20 - 12-11-2016 13:33:24
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâtaeu 129
Testé sur plan, il me semble que la formule pour le périmètre est correcte.
Et pour la formule pour l'aire, c'est assez évident que les différentes hauteurs sont en relation directe avec la racine carrée de la hauteur totale. (Attention, j'ai mis V pour racine carrée).
#21 - 12-11-2016 17:26:37
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâreau 129
D'accord ( j'avais mal lu ) , il ne reste plus qu'à résoudre cette équation 
Vasimolo
#22 - 12-11-2016 18:01:40
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
hâteau 129
Résolu par complément du message initial.
#23 - 12-11-2016 18:15:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâreau 129
Ok Nodgim , j'avais fait pareil 
Vasimolo
#24 - 12-11-2016 18:53:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteau 29
J'ai vraiment aimé cette énigme.
C'est surtout le résultat du partage en périmètres égaux qui est surprenant: la première découpe du haut ne va jamais au delà du tiers de la hauteur ( en partant du bas) et ensuite ça tombe très vite vers des valeurs proches de zéro quand n grandit.
#25 - 12-11-2016 19:23:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
|
 |

 Accueil
Accueil
 Forum
Forum