Bonsoir ,

La première question est en effet très classique ( et pas évidente ) , la solution est donnée par les nombres de Catalan .

Je n'ai pas regardé la deuxième question , je suppose que certains points sont strictement à l'intérieur de l'enveloppe convexe de l'ensemble .

Vasimolo

@Caduk: j'ai apporté une précision: polygones non symétriques.

Si j'ai bien compris la question, il s'agit des nombres de Catalan. C'est un problème très classique : https://en.wikipedia.org/wiki/Catalan_n … binatorics
Ici, pour un ennéagone, la réponse attendue est 429.

Pour la question de la parité des nombres de Catalan, je vous livre une démo qui n'est pas de moi mais que j'aime beaucoup.

Tout d'abord, le nombre de Catalan Cn = (2n)! / n!.(n+1)! permet de dénombrer les chemins de longueur 2n, comme dans la figure 1, qui commencent et terminent sur la droite, et limités au demi-plan supérieur. Par exemple, il y a C5=42 chemins de longueur 10 du type de celui de la figure 1.



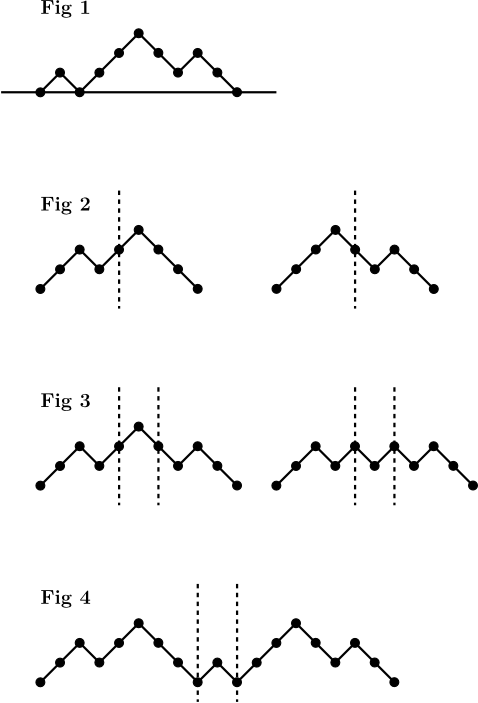
Ces chemins peuvent être assemblés par paires, comme ceux de la figure 2, sauf ceux qui sont symétriques. Donc en notant Sn le nombre de chemins symétriques de longueur 2, Cn et Sn ont la même parité.

Maintenant, les chemins symétriques peuvent également être assemblés par paires, comme sur la figure 3, en inversant la portion constituée des deux segments médians. Mais là encore, il reste des chemins : ce sont ceux pour lesquels la portion médiane est tout en bas, comme dans la figure 4. Or, on peut dénombrer ces exceptions : il y en a C((n-1)/2) si n est impair (car les n-1 segments de gauche déterminent entièrement la figure 4), et 0 si n est pair.
Donc, là encore, Sn a la même parité que C((n-1)/2) si n est impair, et Sn est pair si n est pair.

En résumé, Cn a la même parité que C((n-1)/2) si n est impair, et Cn est pair si n est pair. Par récurrence, Cn est impair si et seulement si n est de la forme 2^k-1.

Pour ton nuage de points, je ne suis pas sûr de la définition du "polygone qui enferme ce nuage" : est-ce que un carré, ou une étoile à 4 branches aplatie en bas, ou autre chose ? Car on peut imaginer des manières plus pathologiques d'enfermer le nuage...

Salut,

Sauf erreur pour un [latex]9[/latex]-gone convexe il existe [latex]429[/latex] découpes possibles.

Plus généralement la suite définie par :
[TeX]U_2=1[/TeX]
[TeX]U_n=\sum_{k=2}^{n-1}U_kU_{n+1-k}[/TeX]
Donne au rang [latex]n[/latex] le nombre de découpes possibles pour un [latex]n[/latex]-gone convexe.

On remarque que la somme, qui contient [latex]n-2[/latex] termes, est symétrique donc paire si [latex]n-2[/latex] est pair donc [latex]n[/latex] pair.

A l'inverse lorsque [latex]n[/latex] est impair donc [latex]n+1[/latex] pair la somme n'est pas symétrique à cause du terme [latex]U_{\frac{n+1}{2}}^2[/latex] et sa parité dépends donc de la nature de ce celui-ci.

Par récurrence il vient :

Si [latex]\frac{n+1}{2}[/latex] est pair alors [latex]U_{\frac{n+1}{2}}[/latex] est pair sinon il est de même nature que [latex]U_{\frac{n+3}{4}}[/latex]

...

Au final on conclus que le nombre découpes possibles pour un [latex]n[/latex]-gone convexe est impair si et seulement si [latex]n-1[/latex] est une puissance de [latex]2[/latex].

Pour le découpage du nuage de points, est-on obligé d'utiliser les 9 points ? Par exemple, le découpage du carré en 2 triangles en traçant juste une diagonale est-il valide ?

@ Sydre : c'est parfait pour la 1ère partie de la question, bravo à toi.
@ Ebichu : Idem, après la retouche, c'est OK pour la 1ère partie. Bravo.

Pour le nuage, je tente 92, sans certitude.

Cela correspond à la suite des nombres de Catalan pour k=n-2

Autrement dit, pour 9 sommets le septième nombre de Catalan est 429.

Les seuls nombres de Catalan impair sont pour n = 2x+1.
Pour conserver cette imparité, le terme suivant doit être (2 fois +1) le précédent...

On tombe donc plutôt sur les 2^n-1.

Pour le nuage de points, je trouve 31 possibilités.

C'est revu et corrigé.

Je relance de 14 : pris par le doute suite à ton message, j'ai vérifié ma preuve en refaisant les calculs d'une autre façon, ce qui m'a permis de corriger une erreur.

Mes deux calculs trouvent maintenant le même résultat, et c'est 120

J'espère que je n'aurai pas à tous les tracer pour me justifier. En attendant, je peux déjà dire que 12 segments appartiennent à toutes les triangulations.

@ Caduk: c'est bon pour la première partie, j'imagine que pour le nombre de combis, tu as oublié un chiffre dans ta réponse.

@ Ebichu: Tu en as 14 de plus que moi. Perso, je suis sûr de n'avoir pas de redondant, et, pour autant que j'ai vérifié, il ne m'en manque pas, mais c'est tellement facile d'en oublier....
Ce qui m'intéresse, c'est la méthode, bien sûr.

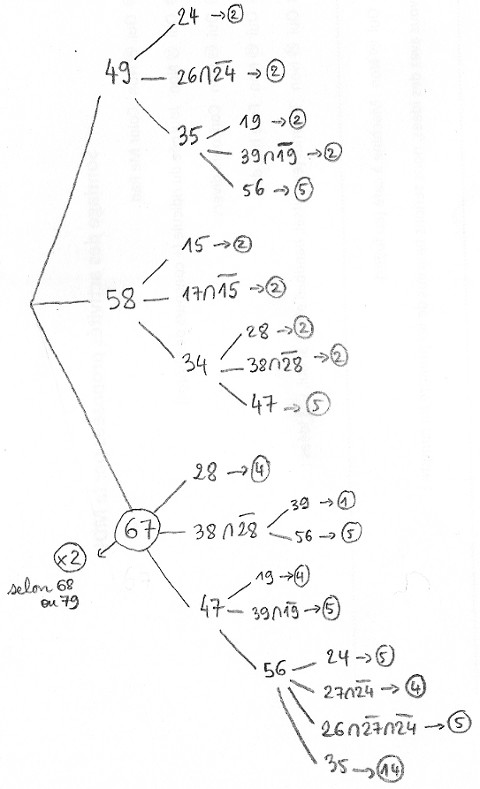
J'ai commencé par remarquer que les arêtes 12, 13, 14, 18, 23, 25, 29, 48, 59, 69, 78, 89 sont obligatoires.

Ensuite, j'ai réalisé un arbre pour répertorier toutes les possibilités. Chaque noeud de l'arbre correspond à une disjonction de cas. Par exemple, il part trois branches de la racine de l'arbre, qui indiquent qu'une triangulation contient soit l'arête 49, soit l'arête 58, soit l'arête 67 (il y en a forcément une et une seule).

Si 49 est tracée, alors 47 et 79 le sont également, ce que je n'ai pas indiqué dans l'arbre. Puis, il y a encore 3 cas : ou bien 24 est tracée, ou bien 26 est tracée mais pas 24, ou bien 35 est tracée. On voit à droite de la première feuille de l'arbre que si on trace 49 puis 24, il y a deux triangulations possibles (le nombre entouré).

Enfin, 67 (en bas de l'arbre) est un sommet un peu particulier, car si on trace l'arête 67, alors en bas de la figure, on a le choix entre tracer 68 ou 79 : il faut donc multiplier par 2 le nombre de triangulations qui commencent par 67.

On a donc au total : (2+2+2+2+5) + (2+2+2+2+5) + 2*(4+1+5+4+5+5+4+5+14) = 120 triangulations possibles.