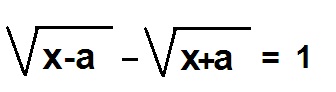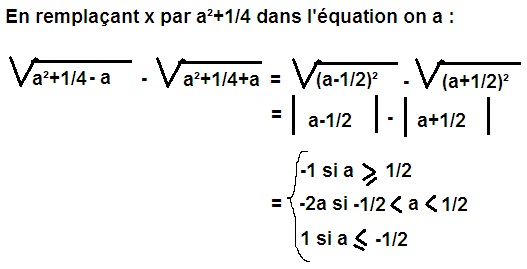Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 03-10-2012 22:51:07
une équation sympzthique !Bonjour,
#0 Pub#2 - 03-10-2012 23:28:57
Une équation symppathique !Bonsoir, J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit. #3 - 03-10-2012 23:41:43
Une équation sympaathique !x-a=1+x+a+2 rac(x+a) The proof of the pudding is in the eating. #4 - 03-10-2012 23:52:53
Un eéquation sympathique !Je trouve un truc bizarre: x = a² +1/4, à la condition que a soit inférieur ou égal à -1/2. Si a est supérieur à 1/2, alors le membre de gauche vaut -1. #5 - 04-10-2012 09:01:05
Une ééquation sympathique !Conditions: il faut que x>=-a et que a<=0 #6 - 04-10-2012 12:37:24
Une équation smpathique !
On additionne (a) + (b) : #7 - 04-10-2012 12:43:49
Une équation sympathique@Gilles : J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit. #8 - 04-10-2012 13:52:56
Une équation symppathique !C'est sur le point (f) que je vais râler.
est toujours valide, donc infirme ce que nous avons fait... Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #9 - 04-10-2012 15:03:58#10 - 04-10-2012 15:45:34
une éqyation sympathique !Bof ! Il suffit de remplacer a par -a et cela marche. #11 - 04-10-2012 16:26:51
Une qéuation sympathique !
@Mathias : sauf votre honneur, dans l'énoncé initial il faut que a ≤ -1/2. J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit. #12 - 05-10-2012 12:29:06
Unee équation sympathique !
Comment arrive-t-on à cette condition ? Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #13 - 05-10-2012 15:27:19#14 - 05-10-2012 15:55:03
Une ééquation sympathique !
Je reprends le raisonnement de Klimrod, en le trafiquant un peu : #15 - 05-10-2012 16:27:15
Une équuation sympathique !Voilà qui est bien reformulé ! Merci ! J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit. #16 - 06-10-2012 13:14:43
une équation sympzthique !En effet Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.