 |
#1 - 20-12-2016 11:35:30
- Bogriga
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 5
patron truangulaire
Peut-on envelopper un cube avec une forme triangulaire, bien sur de façon "one-to-one" c'est à dire tous les points du cube sont couverts par un point et un seul du triangle, tous les points du triangle recouvrent un point et un seul du cube. Pas de plis.
Origine "Town Tournament". Un jeu-concours d'origine Russe. La réponse intuitive est NON. Je sais commencer : un sommet du cube ne peut pas être recouvert par un point intérieur du triangle, parce qu'autour d'un tel point, il y a 360° de triangle alors que autour du sommet du cube, 270° de faces de cube. Donc un sommet du cube doit être recouvert par un sommet du triangle, ou un point d'un côté du triangle. Mais après... ce n'est pas si facile. Je cherche, évidement, une démonstration claire... ce n'est pas si facile. Je cherche, évidement, une démonstration claire...
#2 - 20-12-2016 18:16:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
patron triangumaire
J'ai jeté un coup d’œil , c'est joli et pas évident 
Le tournoi des villes a une vocation internationale , il s'est arrêté en France il y a quelques années faute de volontaires pour encadrer l'affaire ( je ne sais pas s'il a repris depuis ) .
J'ai toujours adoré ces petits problèmes qui l'air de rien remuent pas mal de choses .
Je ne suis pas sûr qu'il faille raisonner sur les angles . En tout cas il est clair qu'aucun "nœud" du patron ne peut être à l'intérieur du triangle , après il faut voir .
Vasimolo
#3 - 21-12-2016 09:17:01
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
patron truangulaire
Spoiler : [Afficher le message] Il ne manque pas grand-chose à ton raisonnement pour que ce soit bon.
Autour d'un sommet du cube, il y a effectivement 270°. Si tu le recouvres avec un côté du triangle, cela enlève 180°. Il reste alors 90° que tu dois recouvrir avec au moins un sommet du triangle. Sinon, tu peux aussi recouvrir le sommet du cube avec plusieurs sommets du triangle. Mais dans tous les cas, au moins un sommet du triangle sera accaparé par le sommet du cube.
Il y a 8 sommets dans le cube et seulement 3 dans le triangle, donc il n'y aura pas assez de sommets dans le triangle pour tout le monde...
Ce raisonnement montre d'ailleurs qu'il faudrait au moins un octogone pour que ça fonctionne. Et avec un octogone, ça peut fonctionner : voir par exemple le patron classique du cube, formé de 6 carrés placés en forme de "T", c'est un octogone.
#4 - 21-12-2016 09:28:07
- Bogriga
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 5
pztron triangulaire
J'ai compris et je suis d'accord.
#5 - 21-12-2016 10:29:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Patron trianulaire
J'ai trouvé ça http://www.diophante.fr/problemes-par-t … n-triangle qui reprend et prolonge les idées déjà développées .
Une question bonus :
On accepte les chevauchements et les fentes dans le patron ( à condition qu'il reste d'un seul tenant ) . Quelle aire minimale faut-il prévoir au triangle pour qu'il puisse recouvrir complètement les six faces du cube d'arête 1 ?
Vasimolo
#6 - 21-12-2016 12:35:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
patron trianhulaire
Pour le bonus voilà ce que j'ai trouvé de mieux :
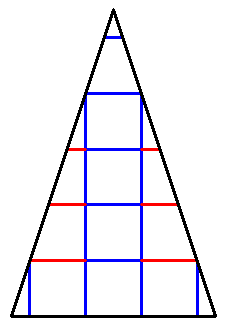
Le patron du cube préexiste dans le triangle ( on peut découper le triangle en conservant un patron du cube ) . Est-ce toujours vrai ou peut-on imaginer un triangle ne contenant aucun patron du cube mais pouvant le former ?
La question est sûrement très con ( un peu comme moi depuis un moment  ) )
Vasimolo
#7 - 21-12-2016 13:21:41
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
oatron triangulaire
Mon idée, plus générale, serait de prouver qu'il est impossible d'envelopper un volume avec un polygone convexe.
#8 - 21-12-2016 14:29:12
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
patrpn triangulaire
Ca parait compromis avec une pyramide à base triangulaire... (tetraèdre, dont le patron est un triangle ) .
#9 - 21-12-2016 15:40:43
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Patron trianggulaire
Voilà de quoi répondre à ta question Vasimolo :
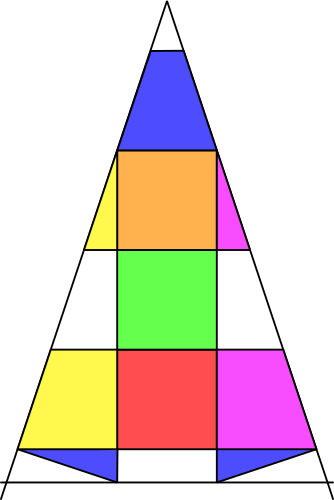
Au passage, si on considère que le cube est de côté 1, mon triangle a pour aire 841/108 soit environ 7,787. Le minimum théorique étant de 6, il y a sans doute encore de la place pour améliorer cela.
#10 - 21-12-2016 17:28:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
patron triangumaire
Joli Ebichu 
A part le tétraèdre , un autre patron convexe ?
Vasimolo
#11 - 21-12-2016 19:05:24
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
pztron triangulaire
Je suppose que si je propose le carré (patron du tore), on va dire que je triche 
#12 - 21-12-2016 19:16:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#13 - 22-12-2016 17:28:18
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Patron triangualire
Je reviens à la question bonus. J'ai amélioré le patron au prix d'une astuce de découpage, et on obtient désormais 361/48 soit environ 7,52.
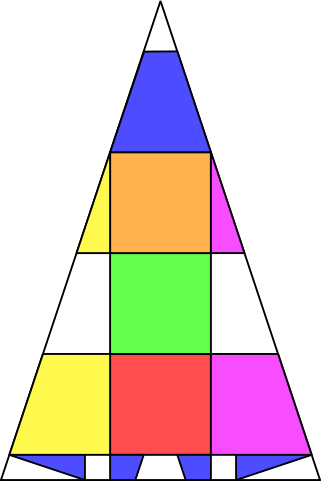
C'est un problème ouvert sans doute très riche !
#14 - 22-12-2016 20:44:23
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
patron trianfulaire
Si on n'accepte pas de chevauchements, on peut se poser la question de combien de triangles il nous faut pour recouvrir un cube...
Il est tres facile de le faire avec 4 triangles, mais peut-on le faire avec 3 seulement. Theoriquement, 3 triangles ont en commun un total de 9 cotés, et on sait qu'il nous faut au moins un octogone, donc serait possible?
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#15 - 22-12-2016 21:28:31
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
pztron triangulaire
c'est exactement ce que propose d'infirmer le lien du message 5
#16 - 23-12-2016 12:42:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Patron tringulaire
@Ebichu,
bravo pour le petit perfectionnement ( à peine plus d'une face et demi perdue en coupe , il sera très difficile de faire mieux ) . Le triangle est construit sur l'un des onze patrons du cube les dix autres étant bien moins performants . J'ai cherché un peu de références sur la toile sans succès .
Sans vouloir ajouter un bonus au bonus , la recherche du meilleur "patron" taillé dans une feuille carrée ou rectangulaire ne manque pas d'intérêt , elle non plus .
Vasimolo
#17 - 23-12-2016 16:15:22
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Patroon triangulaire
Bonjour, voici ma recherche

L'aire de ce triangle est de 7.7511953942878
Ses mensurations sont de 0.2612924 pour la distance entre le bas du carré rouge et le bas du triangle, de 4.78388 pour la distance entre le bas du carré rouge et le sommet supérieur du triangle, et sa demi-base est égale à 1.5363588753256
On obtient donc très légèrement mieux que le premier avec ce découpage. En utilisant l'astuce d'Ebichu pour améliorer son découpage, on obtient 0.2023918959 pour la distance entre le bas du carré rouge et le bas du triangle
Etonnament, on obtient donc une nouvelle aire de 7.6607030820299, donc moins bien que la meilleure solution trouvée...
J'ai essayé de calculer le minimum en prenant directement en compte le découpage optimal, mais mes calculs n'ont jamais aboutis sur wolfram alpha. Quand à le calculer à la main, le système est trop complexe pour obtenir une formule analytique simple.
Conclusion: il y a peut être une forme optimale pas loin de ça, mais bien dure à calculer...
Sinon, il faut révolutionner le découpage, mais je n'ai rien trouvé de mieux...
Pour ouvrir la recherche sur le rectangle, sans avoir trop creusé, o trouve un aire de 8 en mettant 4 carrés d'affilés et 4 rectangles sur les côtés du patron. C'est moins bien que le triangle donc on doit surement pouvoir améliorer...
#18 - 26-12-2016 11:05:52
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
parron triangulaire
On peut faire 7,2 faces en rusant un peu :

#19 - 26-12-2016 11:12:59
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Patron triangulaaire
J'ai un doute sur le carré bleu, es tu sûr qu'il formera un carré après repliement ?(qu'il soit collé au coté bleu ou vert, le triangle bleu en bas à gauche ne semble pas se disposer au bon endroit...)
Edit:
Bon, l'aire de la zone bleue est de toute manière supérieure à 1.
Mais en déplaçant et en rétrécissant le triangle bleu, je pense que l'on conserve une bonne forme...
Edit:
En fait, il suffit de réduire les triangles bleus, et tout tient dans le même rectangle, on trouve donc bien une aire de 7,2
#20 - 26-12-2016 12:07:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Patron triangualire
Super astucieux le triangle bleu : bien vu Gwen !
Vasimolo
#21 - 26-12-2016 17:24:13
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Patron triangualire
Ce qui m'étonne c'est de ne pas réussir à le transformer en triangle...
|
 |

 Accueil
Accueil
 Forum
Forum









