|
#1 - 18-05-2016 18:40:47
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Billar triangulaire
Bonjour à tous.
Sur mon billard (un triangle équilatéral de côté 1), j'ai placé une boule, initialement collée à un des 3 côtés du billard. La boule est supposée ponctuelle ; elle est tirée sans effet, et de sorte qu'elle ne rencontre jamais un des 3 sommets du triangle.
Après 8 rebonds, elle est revenue au point de départ, après avoir effectué un trajet de longueur 4 exactement (les contacts initiaux et finaux avec le côté du triangle ne comptent pas comme rebonds).
Pouvez-vous déterminer la position initiale de la boule, et l'angle avec lequel elle a été tirée ?
#2 - 19-05-2016 12:55:07
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
billard truangulaire
Salut Ebichu,
Si tu confirmes que la position initiale de la boule est à une distance 2-V(7/3) du sommet le plus proche, je chercherais l'angle après, et je donnerais un peu d'explications.
#3 - 19-05-2016 15:08:21
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Billlard triangulaire
@nodgim : c'est la bonne réponse, bravo ! Je veux bien les explications 
#4 - 19-05-2016 18:02:31
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
billard teiangulaire
Elle a été tirée d'un point situé à 0,54138... d'un sommet selon un angle de 79,49...°
#5 - 19-05-2016 18:10:21
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
billard triangumaire
Bon alors la méthode:
Comme dans le billard rectangulaire, l'astuce est bien entendu de vérifier si cette trajectoire en rebonds n'est pas assimilable à une ligne droite. Et en effet, un tout petit peu de géométrie nous apprend qu'on peut effectivement faire un réseau de triangles équilatéraux dans lequel la trajectoire de la balle est une ligne droite.
Pour s'y retrouver dans ce réseau, on numérote les sommets 1,2 et 3. Quand on a numéroté le 1er, tous les autres se déduisent en complétant le sommet manquant de chaque triangle voisin.
En partant d'un segment entre les sommets 1/2, il faut arriver sur un autre segment 1/2. Par tatônnement, on repère une longueur 4 qui semble convenir, avec 8 triangles traversés, entre: si on part d'un repère zéro avec un x horizontal et un y incliné à 30° NE , le 5 ème segment horizontal à gauche sur l'axe x d'une part, le 2ème segment vers le haut sur l'axe y d'autre part, on présuppose une solution. Reste à trouver l'emplacement exact du point.
On pose les données du triangle formé:
-2 segments de longueur 2-x et 4+x formant un angle de 60°
-le 3ème segment de longueur 4.
On a alors toutes les données pour résoudre.
Si je n'ai pas fait d'erreur l'angle de visée est de 38,8° environ avec l'horizontale.
#6 - 19-05-2016 20:07:36
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Billad triangulaire
@nodgim : tout à fait d'accord pour le 1er paragraphe. Après, j'ai plus de mal à suivre, mais comme tu trouves le bon résultat, tes calculs doivent être corrects. Sauf pour l'angle ; tu es sûr de ta valeur ?
@gwen27 : ce n'est pas loin, mais je ne trouve pas tout à fait ça. Tu as une explication pour tes valeurs ?
#7 - 19-05-2016 20:17:58
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Billard trianguaire
Oui. 
Le théorème de Pithagore.
Des rebonds dans un triangle, c'est une ligne droite dans un pavage triangulaire.
Je tombe sur [ rac(37) - 5 ] /2
Pour le calcul de l'arc sinus, j'ai fait confiance à wolfram.
Les côté de même couleur sont les mêmes, j'ai juste essayé de caser 4 de longueur.

#8 - 19-05-2016 21:04:19
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Billard triiangulaire
Mais j'ai pu me tromper...
Sauf erreur, ( (1-x) (1+cos60) )^2 + (2 rac(3) + (1-x) sin60)^2 = 16
Et effectivement, ça fait 2 - rac (7/3) = 0,472474768...
#9 - 19-05-2016 21:12:04
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Billard trianngulaire
@gwen27 : Là on est d'accord, c'est bon 
#10 - 20-05-2016 09:00:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Billrd triangulaire
Un petit 18,6° semble meilleur que ce 38,8°....
#11 - 20-05-2016 10:20:20
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
billard ttiangulaire
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#12 - 21-05-2016 11:59:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
billard triangulaure
@nodgim : tout à fait !
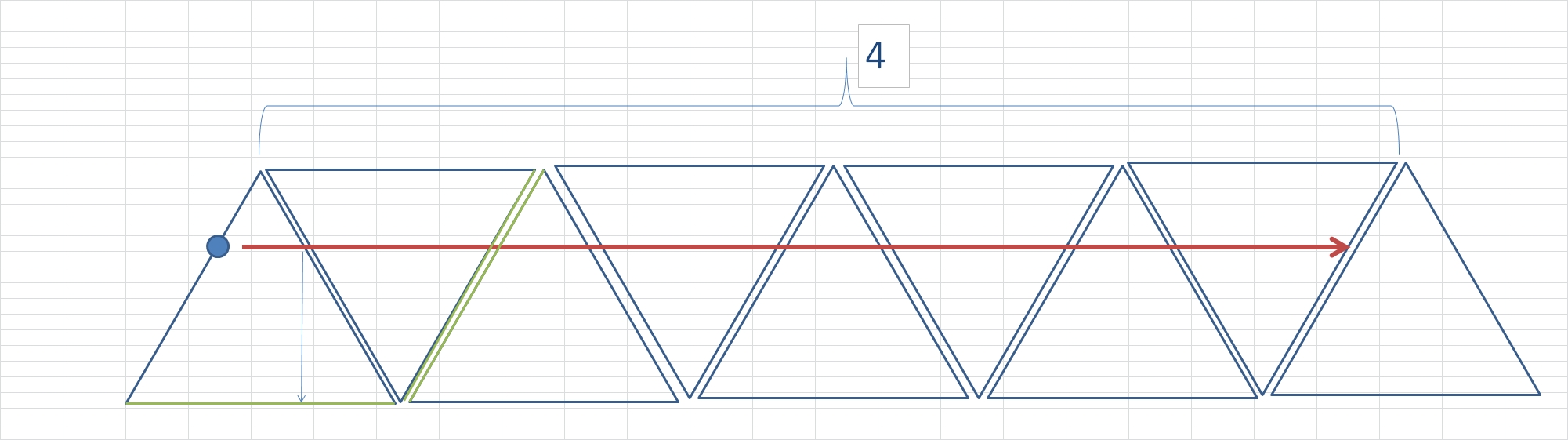
@NickoGecko : il y a "erreur", justement : sur ton dessin, dans le premier triangle, la boule bleue, après le premier rebond, n'a pas une trajectoire verticale, mais une trajectoire parallèle au côté gauche du premier triangle. Si tu complètes la trajectoire de ta boule bleue dans le premier triangle, au bout d'une distance de 4, elle n'est pas au point de départ.
#13 - 21-05-2016 19:16:04
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Billard riangulaire
Je trouve une solution:
La position initiale est de 2−√213 = 0.472474 a partir du sommet le plus proche, et l'angle est de acos(√21−32) = 78.59037789°.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#14 - 21-05-2016 22:48:25
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Billard trianglaire
@dhrm77 : oui, bravo ! Comment as-tu fait ?
#15 - 22-05-2016 00:47:08
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
nillard triangulaire
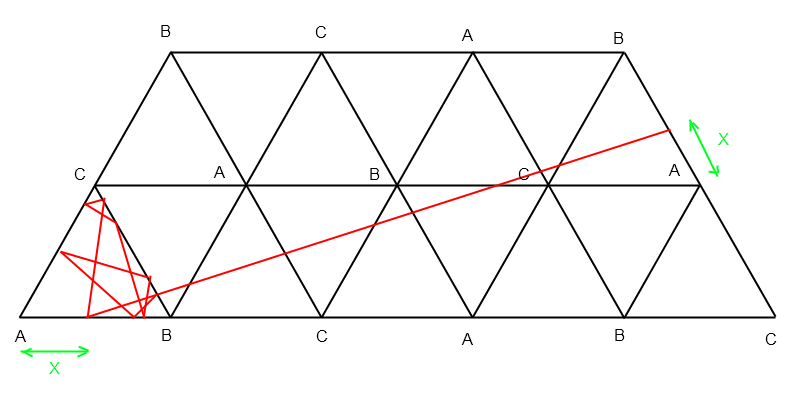
Dx = 9/2 – x – x/2 = 3.(3–x)/2
Dy = V3/2 + V3.x/2 = V3.(1+x)/2
Dx² + Dy² = 4² => 9.(3–x)² + 3.(1+x)² = 64
=> 3.x² – 12.x + 5 = 0 => x = 2–V21/3 = 0,4725 env.
(en ne gardant que la racine comprise entre 0 et 1)
Angle = arctan(Dy/Dx) = arctan(V7–4.V3/3) = 18,6° env.
#16 - 22-05-2016 05:20:33
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
BBillard triangulaire
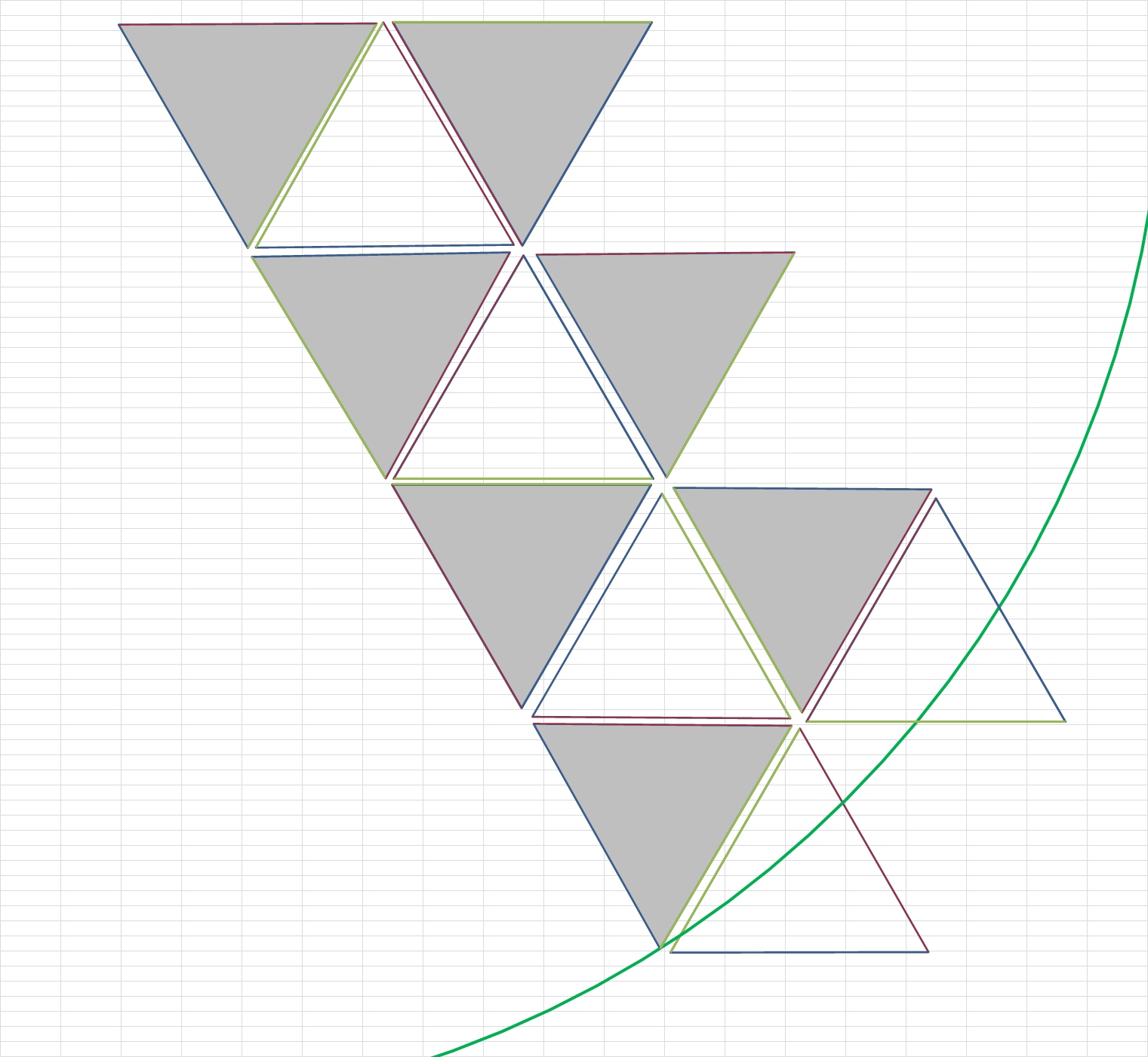
J'ai simplement fait un dessin a la main, de plein de triangles equilateraux juxtaposé qui representent les reflexions de la boule sur plusieurs cotés consécutifs.
Ensuite j'ai placé un point sur un coté, et determiné le point equivalent sur toutes les autres reflexions de ce triangle.
Ensuite j'ai tracé une ligne droite entre 2 points qui traversent 8 cotés de triangles.
Ensuite j'ai calculé la distance entre le point et le sommet, sachant que la ligne droite fait 4, ca m'a donné l'équation dont la solution est plus haut.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#17 - 22-05-2016 05:32:12
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
bilkard triangulaire
En fait cette mèthode marche très bien pour des billards de forme triangulaire equilaterale, carrée ou hexagonale. Mais comment faire si le billard a la forme d'un triangle non-equilateral, d'un pentagone d'un heptagone, ou tout autre forme à huit cotés ou plus?
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#18 - 22-05-2016 10:55:34
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Billard trianglaire
@Franky1103 : parfait ! Joli dessin 
@dhrm77 : je dirais que ça marche aussi. Il suffit de ne pas avoir peur de faire un dessin où les polygones se superposent. Il y a une infinité d'emplacements de polygones possibles, mais il n'y en a que quelques uns qui correspondent à une trajectoire en ligne droite.
#19 - 22-05-2016 12:26:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
billard truangulaire
Bonjour Ebichu
Comme dans beaucoup de problèmes de billards il faut « développer » la trajectoire . Les huit rebonds imposent une trajectoire de type « bleue »
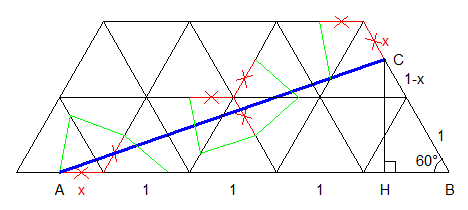
Je n’ai pas le courage de construire la trajectoire dans le billard initial ( en bas à gauche ) , l’idée principale étant que les segments rouges sont tous isométriques .
La propriété de Pythagore dans ACH nous donne x=√73−1≈0,53 . La suite est facile l’angle ^CAH vaut arcos(0,75(1+√73)) soit environ 18,6° .
Ça nous change un peu des billards rectangulaires 
Vasimolo
#20 - 22-05-2016 15:03:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Billard triangularie
@Vasimolo : très bien également !
#21 - 22-05-2016 15:46:51
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
billard trizngulaire
Bonjour,
Je pense avoir une solution.
Le billard est représenté par le triangle ABC. La boule part du point P, sur le côté AB, tel que AP=√7/3−1. Le premier rebond a lieu au point Q, sur le côté AC, tel que tan(PA,PQ)=√7+(4/3)√3.
#22 - 22-05-2016 18:38:17
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Bilard triangulaire
@enigmatus : c'est bon ! une explication ?
#23 - 22-05-2016 19:25:54
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Billard trianulaire
Ebichu #22 a écrit:c'est bon ! une explication ?
C'est du tâtonnement. J'ai tracé un réseau de triangles équilatéraux de côté 1, choisi un segment de départ, et tracé 2 cercles de rayon 4 centrés chacun à une extrémité du segment, pour savoir à peu près où chercher le segment d'arrivée. Ce dernier doit aussi être homoloque au segment de départ, et il faut tenir compte de son orientation.
Il a ensuite fallu calculer la position du point de départ pour que la distance entre les points homologues des segments d'arrivée et de départ soit 4.
Pour finir, un tracé avec gnuplot pour vérifier que la solution trouvée était bonne.
#24 - 22-05-2016 21:52:09
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
illard triangulaire
@enigmatus : OK, très bien.
#25 - 23-05-2016 07:51:21
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
biklard triangulaire
Suite du #21 :
Le huitième rebond a lieu sur le côté AC, en un point R tel que tan(PA,PR)=√7−(4/3)√3. On en déduit que l'angle (PQ,PR)=60° (ce qui se voyait d'ailleurs sur le réseau triangulaire).
Commencer à lancer la boule en direction de R est évidemment une autre solution.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum