 |
#26 - 02-02-2018 17:14:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteaau 149
En fait la migration des pépites est assez bien canalisée , on progresse ligne par ligne et/ou colonne par colonne , et on vire ou on aspire des pépites de la ligne ou la colonne voisine pour combler le déficit ou l'excédent . Pour cela on a presque trop de pépites à notre disposition mais il est difficile d'expliquer pourquoi la même pépite ne va pas être utilisée pour équilibrer à la fois les lignes et les colonnes .
Il reste juste ce point qui accroche mais le diable se cache souvent dans les détails .
Vasimolo
#27 - 11-02-2018 17:26:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtea 149
J'ai une démonstration complète que je dois mettre au propre . En fait c'est celle d'Ocha ( lien fourni ) , j'ai simplement comblé les multiples lacunes 
Je rédige ça dans la semaine .
Il est vraiment joli ce problème !!!
Vasimolo
#28 - 17-02-2018 18:57:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#29 - 18-02-2018 19:14:01
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteaau 149
J'ai un peu de mal à comprendre la preuve. Tu vas peut-être pouvoir m'apporter quelques éclaircissements.
Première question : en bas de la 1e page, sur ton dessin, tu ne traces qu'une partie des flèches, concernant seulement une partie des pépites placées dans chaque angle. Peux-tu expliciter la règle qui fait que tu traces ou non telle ou telle flèche ?
#30 - 18-02-2018 21:39:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 19
On équilibre les lignes en montant des pépites de la ligne k à la ligne k+1 en passant par des pièces "montantes" de la ligne k ou en descendant des pépites de la ligne k+1 à la ligne k en passant par des pièces "descendantes" de la ligne k+1 . Le même procédé est utilisé pour les colonnes .
Vasimolo
#31 - 19-02-2018 18:41:03
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâreau 149
Ça ne répond pas à ma question, je vais la reformuler.
Dans ton exemple, de gauche à droite, les colonnes contiennent initialement 2,2,3,1,1,3 pépites, et de haut en bas, les lignes contiennent initialement 3,1,2,2,1,3 pépites. J'en déduis que c'est pour cela que tu ne traces que les flèches qui vont d'une ligne à 3 pépites vers une ligne à 1 pépite, et idem pour les colonnes.
Mais, en général, quelle règle emploies-tu pour savoir quelles flèches tracer ? Ce n'est pas si évident. Par exemple, j'ai sous la main un exemple de gâteau de taille 12x12, où les les trois premières lignes contiennent respectivement 6, 3 et 4 pépites. Chaque ligne devant contenir 4 pépites à la fin, cela implique qu'il faut tracer des flèches allant de la ligne à 3 pépites vers la ligne à 4 pépites...
#32 - 19-02-2018 19:03:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
âGteau 149
En fait je trace toutes les flèches qui vont dans le sens de l'équilibre ( même s'il y en a trop et c'est toujours le cas ) mais jamais les autres . Après il faut faire un tri et c'est là que le graphe intervient .
Vasimolo
#33 - 20-02-2018 22:53:30
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâtea u149
Donc, si je comprends bien, tu regardes les lignes 1 à k : si elles contiennent plus de 3k pépites, tu traces les flèches [ligne k]--->[ligne k+1], si elles contiennent moins de 3k pépites, tu traces les flèches [ligne k+1]--->[ligne k], et si elles contiennent 3k pépites exactement, tu ne traces pas de flèche entre la ligne k et la ligne k+1. Et idem pour les colonnes.
Si c'est bien cela, c'est OK pour la première page.
Pour la page 2, il faut encore que j'y réfléchisse. Pourrais-tu fournir un exemple avec un gâteau plus grand que 6x6 ? Je pense que ça aiderait vraiment.
#34 - 21-02-2018 10:33:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
gâreau 149
Plutôt destructrice cette énigme....
J'avais un copain cycliste qui se faisait traiter d'assassin quand il nous accompagnait dans les entraînements. Le genre à se mettre en tête et à accélérer imperceptiblement jusqu'à ce que plus personne ne puisse le suivre.
Il ne le faisait pas exprès, il roulait à son niveau.
Cette petite digression pour dire que si on se frotte à des énigmes un peu trop costaudes pour notre niveau, c'est plus destructeur que formateur.
#35 - 21-02-2018 16:14:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
GGâteau 149
@Ebichu : Tu as bien compris et il n'y a rien de difficile dans la deuxième page même si l'idée de départ n'est pas évidente . On fait des chemins reliant les pépites d'angle pouvant bouger aux lignes et colonnes susceptibles de les accueillir jusqu'à saturer le graphe ( chaque arête doit être utilisée une fois et une seule ) . Après on alimente les lignes et les colonnes en utilisant les chemins mais c'est une autre affaire : la construction des chemins est-elle claire ?
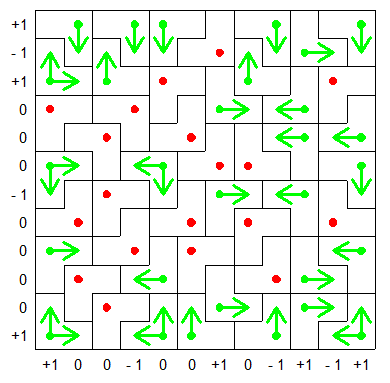
Un exemple avec une grille 12X12 : Il y a 29 pépites susceptibles de bouger , 3 lignes et 5 colonnes pour les accueillir ( les nombres indiquent l'excédent ou le déficit dans la progression ligne par ligne ou colonne par colonne ) . Quels chemins pour illustrer cette configuration ?
@Nodgim : Un peu d'accord , j'ai des tas de problèmes qui me titillent depuis des années et que je ressors régulièrement , souvent pour pas grand chose , mais il m'arrive parfois d'avoir un flash . Il ne faut pas viser trop haut , juste un peu plus haut que ce qu'on sait faire .
Vasimolo
#36 - 22-02-2018 18:06:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâeau 149
En fait la configuration est assez pauvre , seules 6 pépites ont le choix entre deux directions :
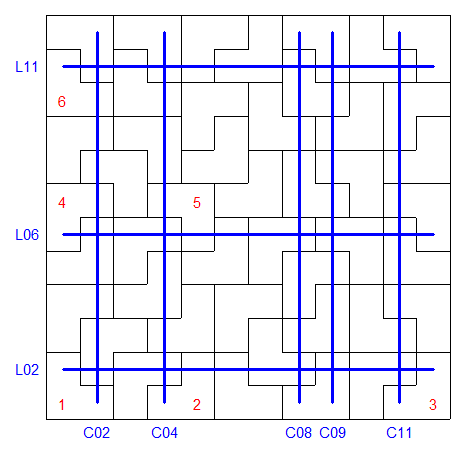
Hormis les déplacements triviaux il ne reste que deux chemins , par exemple :
[TeX]\\[/TeX]
[TeX]L11 \rightarrow 6 \rightarrow C02[/TeX]
[TeX]\\[/TeX]
[TeX]L02 \rightarrow 1 \rightarrow C02 \rightarrow 4 \rightarrow L06 \rightarrow 5 \rightarrow C04 \rightarrow 2 \rightarrow L02 \rightarrow 3 \rightarrow C11[/TeX]
Chaque case d'angle est liée à la ligne et à la colonne quelle peut atteindre .
Ensuite on considère les déplacements de pépites :
[TeX]\\[/TeX]
[TeX] 6 \rightarrow C02 , 1 \rightarrow C02 , 4 \rightarrow L06 , 5 \rightarrow C04 , 2 \rightarrow L02 , 3 \rightarrow C11[/TeX]
Les déplacements ne sont pas nécessairement effectués mais ils sont tous possibles simultanément .
Jusque là est-ce clair ?
Vasimolo
#37 - 22-02-2018 22:57:57
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 1149
Oui, c'est clair  J'ai compris ce qui, en général (pour tout gâteau) permet d'écrire quelque chose de similaire à ce que tu as écrit jusqu'à maintenant. J'attends de voir comment tu conclus. J'ai compris ce qui, en général (pour tout gâteau) permet d'écrire quelque chose de similaire à ce que tu as écrit jusqu'à maintenant. J'attends de voir comment tu conclus.
Un détail : pourquoi avoir tracé C08 et C09 sur ton dessin ?
#38 - 22-02-2018 23:23:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
hâteau 149
Une réponse rapide car je travaille demain 
Au départ j'avais dessiné l'ensemble des chemins y compris ceux constitués d'une seule arête dans lesquels les colonnes C08 et C09 interviennent . J'ai préféré ne pas faire figurer ces chemins pour simplifier la lecture mais j'ai laissé ces colonnes ( j'ai hésité ) .
Une chose importante pour la suite : deux chemins non triviaux ne peuvent pas partager la même extrémité .
Je donnerai la suite demain , tu ne devrais pas avoir du mal à l'accepter car tu as admis le plus difficile .
Vasimolo
#39 - 23-02-2018 17:11:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâetau 149
Récapitulons avant de donner la fin de la démonstration :
1°) On place les pépites dans les angles .
2°) Pour équilibrer la ligne [latex]k[/latex] on va selon les cas , monter [latex]\frac{h_k-b_{k+1}}{3}[/latex] pépites de la ligne [latex]k[/latex] à la ligne [latex]k+1[/latex] ou descendre [latex]\frac{b_{k+1}-h_k}{3}[/latex] pépites de la ligne [latex]k+1[/latex] à la ligne [latex]k[/latex] . Pour réaliser cet équilibre on a au moins trois pièces à notre disposition pour chaque déplacement .
3°) Même chose avec les colonnes en remplaçant bas et haut par gauche et droite .
4°) On relie les pépites qu'on peut déplacer pour réaliser les équilibres souhaités en 2°) et 3°) aux lignes et colonnes pouvant les accueillir .
5°) On ne touche pas aux arêtes des cases de degré 1 ( un seul voisin ) .
6°) On partitionne l'ensemble des arêtes restantes en chemins maximaux commençant et finissant par une ligne ou une colonne ( on passe une seule fois par chaque arête ) .
Maintenant , comment finir ?
On conserve chaque arête du 5°) et on supprime alternativement une arête sur deux des chemins définis en 6°) . Chaque case d'angle du graphe est alors reliée à une unique ligne ou colonne et on autorisera uniquement les déplacements de ces cases vers ces lignes ou colonnes . On avait initialement un surplus de pièces à disposition pour réaliser les deux équilibres mais certains conflits pouvaient apparaître : reste-t-il assez de liens pour satisfaire les deux ?
La réponse est clairement oui .
On avait au moins trois fois trop de pièces pour équilibrer chaque ligne ou chaque colonne . Ces lignes ou colonnes ne perdent aucune liaison si elles sont reliées à des cases d'ordre un , elle perde une liaison sur deux si elle figurent à l'intérieur d'un chemin et brutalement une liaison si elles figurent à la mauvaise extrémité d'un parcours . Heureusement elles ne peuvent pas figurer à plus d'une extrémité d'un chemin : il reste donc un nombre suffisant de cases d'angle permettant d'équilibrer les lignes et les colonnes .
Il n'y a plus qu'à choisir les pièces que l'on veut pour réaliser l'équilibre .
Vasimolo
#40 - 24-02-2018 11:33:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#41 - 24-02-2018 19:45:22
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 14
Non, non, attends, je n'ai pas dit que je ne comprenais pas. J'étais parti faire du bois.
D'ailleurs, j'ai compris  Le truc principal qui m'avait échappé, c'est quand tu dis : "pour réaliser cet équilibre on a au moins trois pièces à notre disposition pour chaque déplacement". C'est bien vu, et c'est très utile dans la suite, car dans ton graphe biparti, si une ligne (ou colonne) est de degré d, alors la partition du graphe en chemins puis la conservation d'une arête sur deux permettent de conserver au moins E(d/2) pépites pour reboucher cette ligne. Ça plus les pépites de degré 1, ça suffit amplement à notre bonheur. Le truc principal qui m'avait échappé, c'est quand tu dis : "pour réaliser cet équilibre on a au moins trois pièces à notre disposition pour chaque déplacement". C'est bien vu, et c'est très utile dans la suite, car dans ton graphe biparti, si une ligne (ou colonne) est de degré d, alors la partition du graphe en chemins puis la conservation d'une arête sur deux permettent de conserver au moins E(d/2) pépites pour reboucher cette ligne. Ça plus les pépites de degré 1, ça suffit amplement à notre bonheur.
Bref, là, j'ai compris la totalité de ta preuve. Félicitations pour ce raisonnement, c'était pas du gâteau !
#42 - 24-02-2018 23:12:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gteau 149
En effet l'hiver est tardif mais dur 
Je reste convaincu qu'on peut choisir trois couleurs pour les pépites et mettre une pépite de chaque couleur dans chaque pièce de façon à ce que chaque ligne et chaque colonne contienne le même nombre de pépites de chaque couleur mais tout reste à faire . Il y a aussi le problème que tu as évoqué pour les rectangles .
Personnellement je vais laisser reposer le problème mais toute idée pour ces prolongements sera bienvenue .
Ce n'est pas la première fois que je trouve une solution à un problème qui me chiffonne depuis longtemps en le postant ici : je crois que je vais garder cette habitude .
Si on regarde de près les connaissances mathématiques nécessaires pour comprendre et résoudre le problème , on ne dépasse pas le niveau collège .
Un énorme merci à Ebichu qui a fait l'effort de décrypter mes messages 
Vasimolo
#43 - 25-02-2018 01:01:22
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteua 149
Pour la généralisation aux rectangles, il me semble que ta preuve fonctionne telle qu'elle, non ?
J'ai un problème du même style sous le coude, d'énoncé très simple et de preuve très dure, à ceci près que j'ai trouvé une démonstration (qui n'utilise pas non plus de connaissance mathématique avancée). J'avais envie de le proposer, au cas où quelqu'un trouve une preuve élémentaire, on ne sait jamais. Mais j'hésite, car c'est un cadeau empoisonné. J'ai dû y passer 2 mois avant d'y arriver...
#44 - 25-02-2018 07:59:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtau 149
Tu as raison pour le rectangle, il reste le cas des trois couleurs qui s'annonce bien plus difficile .
Pour ton problème prise 2 tête n'hésite pas , je ne trouverai sans doute pas mais j'aime bien chercher et j'ai un peu de temps libre en ce moment 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









