 |
#1 - 20-03-2019 19:39:16
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
La conjecture d Tantrix
Je sais que bon nombre de conjectures déjà proposées n'ont pas encore trouvé de résolution et que certaines ont attendu plus d'un siècle pour en trouver une.
Je vous propose néanmoins et modestement celle-ci, que j'ai testé sur un bon nombre de cas et que masab sous-entendait dans ses conclusions :
Toute boucle fermée d'une couleur réalisée à partir des 14 pièces de Tantrix comportant les trois mêmes couleurs peut trouver une solution satisfaisant les trois conditions suivantes :
1 : les deux autres couleurs forment des chaînes continues, fermées ou non.
2 : les zones hexagonales situées sur le pourtour de la figure obtenue ne reçoivent pas plus de deux chaînes de couleur identique.
3 : Il ne doit pas y avoir de trou à l'intérieur de la boucle.
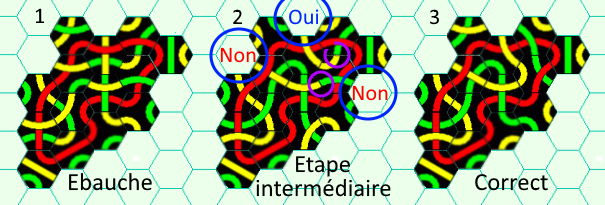
Exemple : A partir d'un contour rouge obtenu sans se soucier des tracés jaunes et verts (fig1), on doit toujours pouvoir aboutir par permutation des tuiles, à un tracé correct respectant ces deux conditions (fig. 3), conditions qui ne sont pas encore respectées à l'étape intermédiaire (fig. 2).
Qui donc pourra, soit démontrer la véracité de cette conjecture, soit trouver un contre-exemple ?
Pour tester, c'est ici
Je vous rappelle que vous pouvez saisir ou déposer une tuile à l'aide du bouton gauche, et la faire pivoter de 60° à l'aide du bouton droit.
#2 - 21-03-2019 20:00:22
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
La conjectur du Tantrix
Salut,
a-t-on le droit de créer la boucle rouge de sorte qu'au milieu de la boucle, il y ait des hexagones vides, sans tuile posée dessus ?
À part ça, j'aurais tendance à répondre à la question par un programme : je pense que le nombre de formes de boucles n'est pas trop important (ça doit se compter à vue de nez en milliers, au pire en millions) et pour chacune, il y a 6! * 6! * 8 = 4147200 façons de poser les tuiles. Donc on est dans des ordres de grandeurs raisonnables pour les machines actuelles. Le plus dur serait de se retrousser les manches pour écrire le programme 
#3 - 22-03-2019 13:15:39
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
La conjecture du Tantrixx
Très bonne question  . Il ne doit pas y avoir de "trou" à l'intérieur de la boucle, ce qui limite légèrement le nombre de solutions. . Il ne doit pas y avoir de "trou" à l'intérieur de la boucle, ce qui limite légèrement le nombre de solutions.
Je rajoute cette condition dans le sujet.
A part ça, pourquoi pas un programme ? On a pu en faire un pour calculer toutes les combinaisons du Pentamino. Je pense qu'il y en a nettement moins dans ce problème. Alors, si cela te tente  ... ...
#4 - 23-03-2019 12:51:23
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
la conjecrure du tantrix
D'après la page suivante, il y a moins de 13224 boucles, "moins" car on interdit les trous.
http://oeis.org/A284869
Donc ça confirme que la principale limitation ne sera ni la mémoire, ni le temps de calcul, mais le temps du programmeur...
#5 - 24-03-2019 10:24:17
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
La coonjecture du Tantrix
Moins car le nombre de type de virage est également limité.
Je réfléchissais plutôt à l'inverse, quel serait le contre exemple, quel est le cas limite qui imposerait le plus de contrainte jusqu'à atteindre le point bloquant.
Avec un trou au milieu, il est facile de trouver un contre exemple, mais la contrainte sans trou rend le problème vraiment difficile à bloquer.
#6 - 24-03-2019 19:25:28
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
La conjecture du Tantri
Moins car le nombre de type de virage est également limité.
En effet, bien vu. Ça reste quand même trop pour traiter tous les cas à la main 
#7 - 24-03-2019 19:46:47
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
La conjjecture du Tantrix
Je me faisais la même réflexion que godisdead, ainsi que celle-ci :
Est-il bien judicieux d'essayer de transposer un réseau triangulaire sur un réseau en hexagones ? En plus, deux tuiles ont un parcours rectiligne, avec des faces parallèles, ce qui rend difficile l'obtention d'un réseau triangulaire...
Voici ce que donne le découpage en un maximum de triangles en conservant les frontières entre les tuiles sur l'exemple que je donnais dans le sujet :
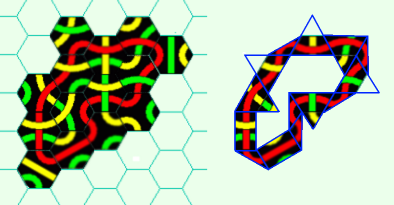
Ce n'est pas à proprement parler un réseau !
Enfin, l’obtention de toutes les configurations de lignes rouges fermées sans tenir compte des autres couleurs, laisse ouverte la conjecture : est-ce qu'il y aura autant de configurations qui respecteront la continuité des autres lignes et le fait que toutes les zones hexagonales du pourtour puissent recevoir (au moins) l'une des 14 tuiles en respectant encore cette continuité ?
#8 - 24-03-2019 21:49:50
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
La onjecture du Tantrix
En fait, un chemin rouge est équivalent à un chemin bleu sur le réseau triangulaire ci-après, il suffit de placer un point bleu au centre de chacun des hexagones :
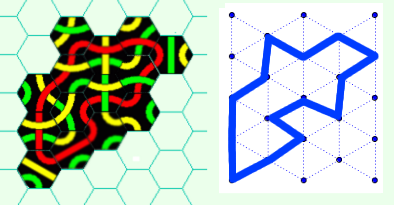
Raté 
#9 - 25-03-2019 11:10:24
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
L aconjecture du Tantrix
Merci pour cette leçon. Décidément, je suis vraiment un piètre amateur en mathématiques  ... ...
Si j'ai bien compris, il faut commencer par repérer parmi les 13224 solutions, celles qui sont sans trous et qui possèdent à la fois 6 angles de 60° et 6 angles de 120°.
Il devrait déjà y en avoir beaucoup moins.
Puis vérifier (désolé d'y revenir, mais c'était le but de ce problème) que toutes ces solutions sont compatibles avec la continuité des deux autres couleurs des 14 tuiles de Tantrix, y compris sur les bords...
#10 - 25-03-2019 13:44:51
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
La conjecture u Tantrix
Oui, c'est bien cela, tu as bien compris le principe. Dans un premier temps, on pourrait essayer de déterminer un nombre plus précis que ce 13224.
#11 - 25-03-2019 15:50:39
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
la conjecture di tantrix
Comme il ne doit pas y avoir de trou à l'intérieur de la boucle, la figure en bleu sur mon message précédent est un polyomino triangulaire à 12 triangles (un dodekiamond), ce qui limite un peu plus le nombre de figures possibles.
https://oeis.org/A070765 donne 3226 telles figures sans trou.
Sur http://www.mathpuzzle.com/12_e.gif sont représentés ces dodekiamonds (y compris ceux avec trou).
Mais parmi toutes ces figures, assez peu ont exactement 6 angles de 60° et 6 angles de 120°...
#12 - 26-03-2019 21:50:29
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Laa conjecture du Tantrix
Encore une belle référence à oeis  ! !
Cependant, si il est vrai que chacune de mes boucles sans trous de 14 tuiles de Tantrix correspond bien à un polyomino triangulaire à 12 triangles, la réciproque n'est peut-être pas toujours vraie. Si je ne m'abuse, certains dodekiamonds peuvent représenter des boucles de 10 ou 12 tuiles.
Par exemple :
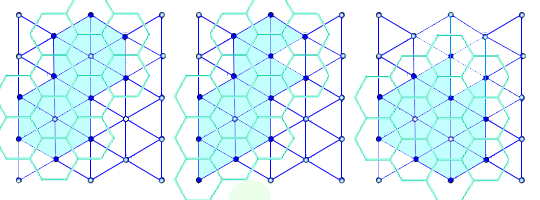
#13 - 29-03-2019 10:23:41
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
La conjecture du Taantrix
Je vais essayer de faire un programme Python pour dessiner toutes les boucles. Ça tombe bien, il faut que j'apprenne à programmer en Python. J'espère juste que tu n'es pas trop pressé 
#14 - 29-03-2019 16:47:21
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
la cobjecture du tantrix
Je ne suis pas du tout, du tout pressé.
Bon courage !
Amuse-toi bien  . .
#15 - 30-03-2019 20:32:41
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
la conjecture di tantrix
Au prix d'un bel effort de procrastination (car j'ai plein de boulot par ailleurs et une fameuse envie de pas le faire), j'ai rédigé un programme. Il trouve 507 boucles, sous réserve d'éventuels bugs.

(enregistrer cette image quelque part pour la voir en plus grand)
Je tiens mon code à disposition de ceux que cela intéresserait, il fait 240 lignes, c'est pour ça que je m'abstiens de le poster (c'est long).
#16 - 31-03-2019 09:38:35
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
La conjecure du Tantrix
Ces 507 boucles sont-elles données à rotation, translation et réflexion près ?
#17 - 31-03-2019 18:13:03
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
#18 - 31-03-2019 22:16:02
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
La connjecture du Tantrix
#19 - 01-04-2019 18:08:28
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
la conjecture su tantrix
Spoiler : [Afficher le message] Mmh, je ne vois pas ce que je casse comme baraque, c'est-à-dire ce que tu comptais faire comme énigmes avec ça ?
Un bug faisait que certaines positions apparaissaient plusieurs fois dans la liste. Il est corrigé, mais il en reste peut-être, prudence...

Ça fait 363 boucles en tout.
#20 - 04-04-2019 22:42:22
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
LLa conjecture du Tantrix
Ebichu a écrit:Je ne vois pas ce que je casse comme baraque, c'est-à-dire ce que tu comptais faire comme énigmes avec ça ?
Peut-être étais-tu passé à coté de mon énigme Tantrix 01, où je demandais de construire des boucles de Tantrix complétant deux pièces déjà posées ?
Le nombre "01" pouvait laisser penser que je comptais en poser au moins 10  ... ...
Spoiler : [Afficher le message] Mais, cela ne fais rien, je vais quand même continuer  ! !
|
 |

 Accueil
Accueil
 Forum
Forum












