(Si je ne me suis pas planté comme d'hab. (sourire)²)
...

Pour les paires orphelines ...
Pour revenir vers un élément générateur on utilise la technique qui correspond à la recherche du PGCD des deux nombres.
Il est la valeur commune trouvée par la méthode des soustractions successives.
(représentation géométrique

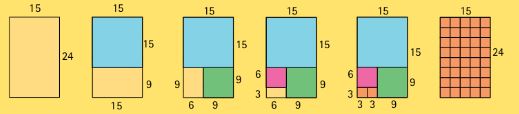
ici revenir de (15,24) ... (3,3))

Si (a,b) est tel que PGCD(a,b) = c alors toutes les paires qui sont dans le même cas "sont familles avec" comme on dit en Lorraine.
donc (il n'y aurait) pas de paires orphelines

Donc (?)
Pour la probabilité que deux paires ne soient pas de la même famille :
je propose 6/π²
?

Salut,
Entend t-on la famille au sens large (éventuellement intergénérationnelle) ou obligatoirement de même génération (comme dans l'exemple donné) ?
(je ne suis d'ailleurs pas certain que cela change le raisonnement)
Bonne journée.

Pour la probabilité, tu n'avais pas demandé dans ton énoncé que l'on justifie sa réponse (sourire)²
(un coup que tu m'as fait je crois (sourire)²² avec un "oui") *
_________

Il y a maintenant ... en prenant du recul, un truc qui me chiffonne
Une paire peut toujours en générer une autre
elle est donc de la famille de cette paire qu'elle génère.

Il n'existe donc pas de paire qui n'est "de la famille d'aucune autre paire"

Faut-il comprendre que tu entends
(Je me dis que ptitours63 a certainement compris ce qui m'échappe là)
"qui n'est générée par aucune paire ?"

à ce compte c'est le cas des paires du type (a,a)
puisque l'antécédant est nécessairement soit
(a, a-a) soit (a-a,a) exclus par ton énoncé. (a et b non nuls)

Merci de ta patience (sourire)²


___
*en rapport avec la probabilité de deux nombres d'être premiers entre eux

Hello ! voici donc les réponses, qui sont les mêmes que celles de ptitours63

A la première question (et bonne réponse d'aunryz aussi sur celle-là) : toute paire (a,b) avec a≠b admet un parent :
* soit a<b et donc le parent était (a,b-a)
* soit a>b et donc le parent était (a-b,b)
(les autres cas donnent des nombres négatifs qui ne sont pas autorisés)
De ce parent, on peut générer une autre paire, soit (b,b-a) soit (a-b,a) suivant les cas, qui sont différentes par construction de la paire initiale : elles sont donc de la même famille.

Si a=b par contre, la paire n'admet pas de parent : ça serait éventuellement (0,b) ou (a,0) si les nombres nuls étaient autorisés, mais ça n'est pas le cas...
Or, comme le précise l'énoncé, "deux paires sont de la même famille si elles ont un ancêtre commun". Les paires qui n'ont pas de parents n'ont a fortiori pas d’ancêtre.

On en déduit que les "paires orphelines" sont celles de la forme (a,a), bien qu'elles soient elles-mêmes les ancêtres d'une infinité d'autres paires.

Pourquoi cette ambiguïté ? Pour aider à mettre le doigt sur quelque chose : le plus haut ancêtre d'une paire quelconque (a,b) est (g,g) où g=pgcd(a,b)
Démonstration en quelques lignes :
- tous les nombres sont des multiples de g par combinaison linéaire de deux entiers
- chaque parent admet un terme plus petit que ses descendants directs
- en remontant le fil, on a donc une suite d'entier décroissante, majorée par 0 exclu et multiple de g, donc majorée par g
--> on arrive à une absurdité via l'argument de descente infinie...
... sauf si on admet que la descente s'arrête, c'est-à-dire que la paire n'a pas de parent. Et comme expliqué ci-dessus, celles qui n'ont pas de parents sont de la forme (n,n), où n est un multiple de g.
Et pour conclure cette démonstration, on ajoute que si n>g, alors a et b seraient eux-mêmes des multiples de n, et donc on aurait un diviseur commun à a et b supérieur à leur pgcd, ce qui serait absurde.

Conclusion : toute paire (a,b) est rattachée à un unique arbre dont la "racine" serait (g,g) avec g=pgcd(a,b)

Ce résultat est utile pour répondre à la seconde question.

La probabilité que a et b aient pour pgcd le nombre k est [latex]P(pgcd(a,b) = k)=\frac{1}{k^2.\zeta(2)}[/latex]

Si vous ne connaissez pas la fonction Zeta, c'est pas hyper grave (elle va sauter 😉)

La probabilité que 2 paires soient rattachées au même arbre de racine (k,k) est donc la probabilité que chacune des paires le soit, autrement dit que le pgcd de chacune des paires soit k
[TeX]P(pgcd(a,b) = k)*P(pgcd(c,d) = k)=\frac{1}{k^4.\zeta(2)^2}[/TeX]
La probabilité totale est donc la somme de tout ça, pour toute valeur de k
[TeX]P=\sum_k\frac{1}{k^4.\zeta(2)^2} = \frac{\zeta(4)}{\zeta(2)^2}[/TeX]
Et pour finir, on peut remplacer la fonction Zeta par sa valeur exacte, qui est connue pour les deux cas particuliers 2 et 4
[TeX]\zeta(2) = \frac{\pi^2}{6}\\
\zeta(4) = \frac{\pi^4}{90}\\
P = \frac{36}{90} = 0.4[/TeX]
Au final donc 40% de chance pour deux paires d'être de la même famille 😊

Wouahou, très joli problème, et très jolie solution. Grâce à vous, je découvre que la fonction Zeta a un rapport avec les PGCD. Si seulement ça pouvait nous aider à trouver tous les zéros de la fonction Zeta !...

Merci Scarta pour l'énigme de haut vol, et les découvertes (pour moi) que cela a engendrées.