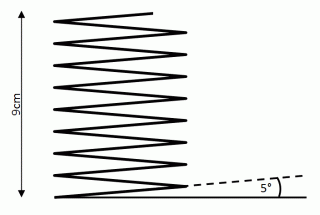
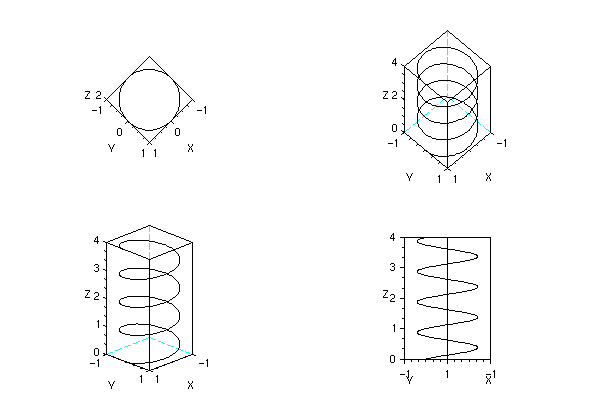
J'appelle D le diamètre d'une spire (donc le diamètre penché). J'appelle α l'angle de 5° (π36).
Si j'appelle h l'élévation d'un demi-tour de spire et l la longueur de fil nécessaire pour ce demi-tour, on a:
hD=sin(α)
Or l=π2D (demi-cercle penché suivant l'angle α)
Donc l=π2hsin(α)
Il faut noter que pour simplifier la compréhension des calculs j'ai pris h égal à un demi-tour mais la proportionnalité reste la même quelque soit h.
En particulier pour h=9 cm, on trouve l~162.2 cm
A première vue, cela semble beaucoup, surtout au regard de la figure mais 5° est un angle très petit. Si ce ressort à un diamètre droit (cylindre circonscrit) de 9 cm aussi par exemple, h~0,79cm et donc une spire entière (un tour complet) permet de monter de ~1,57cm. Il faut donc environ 6 tours complets pour monter de 9cm, soit une longueur d'environ 9∗π∗6/cos(α)≈170, ce qui est bien du même ordre de grandeur.
Pourquoi le diamètre n'intervient pas: si le diamètre est plus grand, l'angle étant fixe, le nombre de spires nécessaires pour atteindre 9cm est plus faible et la longueur totale reste la même.
(J'ai appris a utiliser l'editeur TeX pour les formules  )
)

 Accueil
Accueil
 Forum
Forum