 |
#1 - 22-06-2010 20:05:29
- one_handred
- Habitué de Prise2Tete
- Enigmes résolues : 21
- Messages : 12
Pizza wars ; la dernière part de piizza a partager ...
Bonjour !
Bon voici ma deuxième enigmea propos des pizzas.
(Désolé vasimolo, mais j'ai enfin trouvé le logiciel qu'il me fallait :-/)
C'était il y a quelque année. je rentre de cours de math, ca parlais de trigonometrie et de geometrie. Difficile a l'époque mais j'avais bien compris. Par contre j'avais faim.
quand tout a coup, je vois ma soeur pret a engloutir la derniere part de pizza :
NoOOOOOOOOOOOOOOONOOOOOOoooooN criais-je. D'un commun accord, aidés par le calibre 9mm de papa exedé par tant de cris braqué sur nous, on a decidé de la partager.
Mais comment?
il faut prendre en compte que je possède qu'une règle et une equerre
J'aime la croute et ma soeur non. On decide donc de couper comme sur le schema. (le trait bleu perpendiculaire au trait rouge, a la cote x)
je donne a et b (cf schema).
je veut connaitre x pour que l'aire de nos deux parts soient strictement egales
je rappelle qu'un pizza est ronde a l'origine. celle-ci est supposée parfaite (donc l'arc de cercle fait partie du cercle de centre "le bout pointu de la pizza")
les traits noir representent la pizza
les rouges des traits de construction (celui qui passe par le bout pointu de la part est un bissecteur de l'angle hein !)
le bleu, la maniere dont je compte couper
Bonne chance a tous
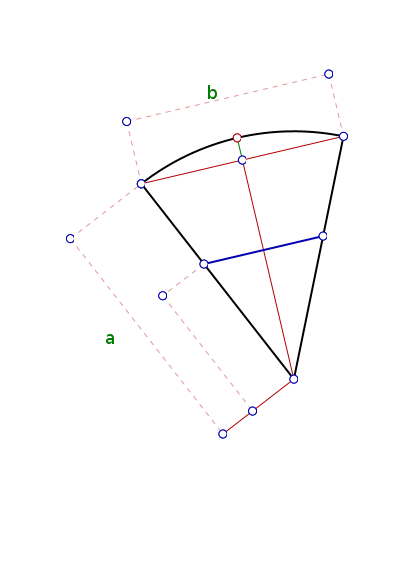
edit : j'ai oublié d'inscrire x, mais ya la cote. elle est dans la meme direction que "a"
j'espere que je suis assez clair. dite moi, je modifiera au cas ou
#2 - 22-06-2010 21:18:07
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Pizza wars ; la dernière prt de pizza a partager ...
vas-y mollo sur les pizzas !
http://enigmusique.blogspot.com/
#3 - 22-06-2010 22:11:34
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Pizza wars ; l adernière part de pizza a partager ...
[edit : oui j'avais mis l'aire de la demie part en m'emmélant les couteaux...et effectivement j'aurais du m'en apercevoir en testant θ→0, mais je me suis dis que x=a/2 était bon, alors que pas du tout... est-ce que c'est bon maintenant ?]
si je note θ le demi angle de la pizza, j'ai :
asinθ=b2
donc
θ=arcsin(b2a)
et les aires sont égales si
x2cosθsinθ=122θ2ππa2=θa22
ie si
x2cosθb2a=θa22
ou sinon en "simplifiant" avec l'identité trigonometrique cela donne :
x2sin2θ=θa2
au final, x=a√θ2cosθb2a=a√aarcsin(b2a)bcos(arcsin(b2a))
ou bien x=a√θsin2θ=a√arcsin(b2a)sin(2arcsin(b2a))
c'est moche mais ca donne le résultat, à condition de garder un angle pas trop grand...
#4 - 22-06-2010 22:59:55
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
Pizza was ; la dernière part de pizza a partager ...
Soit θ la moitié de l'angle de la part de pizza.
Nous avons alors sinθ=b2a, soit θ=arcsinb2a.
La surface totale de la part est θ×b2=b2arcsinb2a
Merci Thales de nous donner la longueur de la coupe : b×xa.
La hauteur du triangle isocèle formant la demi part sans croute est x \times \cos{\theta} = x \times \cos{ (\arcsin{\frac{b} {2a})}
La surface de la demi part sans croute est donc : b×x2×cos(arcsinb2a)2a.
Les demi-parts seront de même surface ssi la surface de la demi-part sans croute fait la moitié de la surface de la part :
b2arcsinb2a2=b×x2×cos(arcsinb2a)2a
Soit x=√a×b×arcsinb2acos(arcsinb2a)
C'est pas beau à mesurer à l'équerre et au compas donc j'imagine que j'ai loupé un calcul ou une simplification 
#5 - 23-06-2010 06:42:58
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
Pizza wars ; la dernière part de pizza a partaager ...
Bonjour
Notons θ l'ouverture angulaire de la part de pizza
On a alors sin(θ2)=b/2a=b2a
Soit θ=2arcsin(b2a)
Soit S la surface de cette part de pizza, a étant le rayon du secteur angulaire
S=θ2a2
On veut donc trouver x tel que la surface du bout "pointu" jusqu'au trait bleu vale S2
La surface du "bout pointu" est xsin(θ2)∗xcos(θ2)
soit x2(sinθ2)
on veut donc x2(sinθ2)=θ4a2
soit x=√θa22sin(θ)
La formule est définie pour θ∈]0;π[ ce qui est en relation avec le domaine de validité de la question.
avec a et b, on détermine θ avec la formule de départ θ=2arcsin(b2a)
> Une application numérique avec a=1 et θ=π4 (proche de l'énoncé)
donne x=0.745 ce qui concorde ...
S=0.393 et S2=0.196
 C'est mon premier post avec des formules LaTex ! C'est mon premier post avec des formules LaTex !
edit : Mise en forme de la formule complète, x exprimé avec a et b seulement en faisant disparaître θ :
\theta = {2 arcsin( \frac b{2a})}
x=√(arcsin(b2a))a2sin(2arcsin(b2a))
et comme sin(2α)=2sin(α)cos(α)
sin(2arcsin(b2a))=2sin(arcsin(b2a))cos(arcsin(b2a))
i.e : sin(2arcsin(b2a))=(ba)cos(arcsin(b2a))
d'où : x=\sqrt{\frac {a^3arcsin( \frac b{2a})}{bcos({arcsin( \frac b{2a})}}
et effectivement comme cos(arcsin(α))=√1−α2
On a :
x=\sqrt{\frac {{a^3arcsin( \frac b{2a})}}{b \sqrt{1-( \frac b{2a})^2}}
x=\sqrt{\frac {2a^4 arcsin( \frac b{2a})} {b \sqrt{4a^2-b^2}
x=a^2\sqrt{\frac {2arcsin( \frac b{2a})} {b \sqrt{4a^2-b^2}
(l'A.N. est vérifiée par cette dernière expression)
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#6 - 23-06-2010 19:09:49
- Khyros
- Habitué de Prise2Tete
- Enigmes résolues : 23
- Messages : 18
Pizza wars ; la dernière part de pizza a partger ...
Il faut d'abord calculer l'angle de cette jolie portion de pizza, pour chopper son aire. Ensuite trouver x en posant que l'aire du triangle vaut la moitié de l'aire de la part...
Ce qui nous fait:
- En nommant A l'angle, on trouve A = (1/2)*arcsin(b/a)
* On peut utiliser le triangle rectangle inscrit dans le cercle en prolongeant le côté a en 2a et en gardant le côté b, ce qui nous permet d'avoir l'angle A/2 avec un joli théorème de 4ème.
- L'aire d'un arc-de-cercle c'est demi-angle*rayon², ici ça fait (1/2*A*a²)
* Pas d'explications à ajouter mais ça faisait joli de mettre une étoile en dessous.
- L'aire d'un triangle c'est demi-base*hauteur, ici ça nous donne (1/2)*sin(A)*x²
* Le demi trait bleu vaut sin(A/2)*x et la hauteur du triangle (bout rouge) vaut cos(A/2)*x en se plaçant dans le triangle rectangle créé par la bissectrice. Donc l'aire vaut sin(A/2)cos(A/2)*x² qui se simplifie en (1/2)*sin(A)*x².
- Finalement on peut poser l'égalité:
(1/2)*sin(A)*x² = (1/4)*A*a²
Soit: x = racine( (A*a²) / (2*sin(A) )
Ou encore avec la valeur exacte de l'angle...
x = racine ( (arcsin(b/a)*a²) / (4*sin( (1/2)*arcsin(b/a) )))
Alors je suis à peu près certain que ça se simplifie joliment avec de la trigo, mais j'ai clairement la flemme.
#7 - 23-06-2010 19:42:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
pieza wars ; la dernière part de pizza a partager ...
Tu es tout pardonné 
Vu les données j'ai bien peur que la construction soit très approximative même en ajoutant un compas et un rapporteur à la liste d'intruments 
Vasimolo
#8 - 23-06-2010 20:07:17
- one_handred
- Habitué de Prise2Tete
- Enigmes résolues : 21
- Messages : 12
pizza wars ; la dernière part de pieza a partager ...
Mon dieu, que vois-je !
Mc flambi et Nicouf on une erreur sur l'aire de la surface totale (ce qui est fortement dommage !)
j'ai pour l'instant deux bonnes réponses.
je n'ai jamais dit que c'etait simple, la formule a la fin n'est forcement jolie. on peut encore l'arranger avec cos(arcsin(x))=sqrt(1-x²) mais c'est un question de gout
dans l'absolu, il me suffit de mesurer a et b, faire l'application numerique (avec une calculette par exmple) et couper au bonne endroit
Pour la petite histoire (c'est une histoire vrai, sauf pour le calibre 9mm de mon pere), ma soeur a mangé la pizza pendant que je faisait les calculs
@vasimolo--> vraiment pas? j'attendais une critique du maitre gateau !!
#9 - 23-06-2010 20:13:32
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
pizza wars ; la dernière part de pizza a partzger ...
Je note α le DEMI-ANGLE de la pointe de la pizza, c la longueur du segment bleu (la ligne de coupe) et d la longueur entre la pointe de la pizza et la ligne bleue.
Commençons:
La surface totale de la part est α.a2 (par définition, α est le DEMI-angle)
La surface de la pointe est c.d2. On cherche donc x tel que c.d2=α.a22(E)
On a: b2a=c2x=sin(α)
Donc c=2x.sin(α)
D'autre part, d=x.cos(α)
Donc c.d=2x2.sin(α)cos(α)=x2.sin(2α)
(E) <=> x2.sin(2α)=α.a2
<=> x2=a22.2αsin(2α)
Il reste à noter que x et a sont positifs, que 2α et sin(2α) sont positifs pour α dans l'intervalle [0,π2]. On peut donc passer à la racine carrée positive.
En notant θ=2α, l'angle de la pointe, on obtient finalement:
x=a.√θ2.sin(θ)
Si on ne veut exprimer la réponse qu'en terme de a et b, θ=2.arcsin(b2a)
Voila, voila, c'était sympa, surtout d'essayer de donner la réponse la plus "compacte" (mais tout en latex, c'est un peu laborieux  ). ).
#10 - 23-06-2010 23:20:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Pizza wars ; la dernière part de pizza a partagre ...
A chacun ses plaisirs 
J'ai fait le calcul et le résultat ne m'emballe pas , je le garde donc pour moi , je préfère quand les découpages se réalisent sans accroc . Tu as bien sûr mon soutien sans faille pour ta série 
Vasimolo
#11 - 25-06-2010 23:07:04
- one_handred
- Habitué de Prise2Tete
- Enigmes résolues : 21
- Messages : 12
Pizza wars ; la derinère part de pizza a partager ...
Bonsoir a tous,
bravo a ce qui ont participé,
on a donc une bonne reponse de rivas, Nickegecko, et khyros
il est vrai que la réponse n'etait pas simple (c'est fou ce qu'on peut se prendre la tete sur un part de pizza)
Le découpage n'était pas si aisé.
pour la prochaine, j'essairai d'avoir un resultat un peu plus sympathique. (c'est ma seconde, j'y vais a taton) pour un découpage sans accroc comme dit vasimolo
A bientot
One_handred
#12 - 25-06-2010 23:56:27
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Pizza wars ; la dernière part de pizzza a partager ...
Bonsoir,
Pour être tout à fait précis, j'ai commis une petite erreur.
Avec mes notations, la surface de la pointe n'est pas c.d comme je l'avais écrit mais c.d2.
J'ai corrigé mon erreur directement dans ma réponse et je trouve donc la même chose que NickoGecko (après avoir sorti 'a' de sous la racine)  et que Khyros (aussi après avoir sorti 'a' de sous la racine). et que Khyros (aussi après avoir sorti 'a' de sous la racine).
Par contre, toujours pour être tout à fait précis, le calcul de 'A' de Khyros me semble incorrect: l'angle n'est pas (1/2)*arcsin(b/a) mais 2.arcsin(b/2a) ce que trouve aussi NickoGecko 
C'était un problème bien sympathique donnant un formule assez belle.
Quand même, je reste intrigué par les limites lorsque θ→0 et θ→π
#13 - 26-06-2010 16:16:17
- Khyros
- Habitué de Prise2Tete
- Enigmes résolues : 23
- Messages : 18
Pizza wars ; la dernièer part de pizza a partager ...
Ahah foui, j'me suis planté comme un bleu sur l'angle, en fait <3
Je trouve donc la même chose que vous après vérification.
Pour ce qui est de la limite en 0, donc a / sqrt(2) je crois, je vois pas bien intuitivement à quoi ça correspond. J'aurais pensé que ça donnerait du (2/3)*a comme pour le centre de gravité puisque quand l'angle tend vers 0 ça s'assimile à un simple triangle.
Mais pour l'angle qui dépasse Pi/2 en tout cas on a pas résolu le problème, et donc la limite en Pi ne signifie rien, puisque la section peut se faire en coupant de la croute pour avoir 2 moitiés égales, alors que là on a calculé la section comme étant l'aire d'un triangle.
#14 - 26-06-2010 19:27:44
- one_handred
- Habitué de Prise2Tete
- Enigmes résolues : 21
- Messages : 12
pizza wars ; la dernière part de pizza a oartager ...
Y'avait peut etre de petite erreur certes.
comme on a besoin de notation intermediaire (a, b , c et theta) et que on peut utiliser thales ou les sinus et cosinus, je ne les ai pas detecté (honte ...)
le principe est de toute facon compris comme dirais mon prof de math 
j'ai juste vue les grosses (et hideuses erreures :p) de calcul d'aire.
je n'ai pas envisagé la cas ou l'angle est superieur a Pi/2, je m'y pencherai peut etre. mais a priori le probleme viendrait du fait qu'on aurait pas theta=arcsin(b/2a) mais un signe moins ou une constante en plus. Il faut voir les modalités de la fonction reciproque de sinus(definit uniquement sur [-Pi/2;Pi/2])
la limite en Pi n'as aucun sens, il n'est plus possible de couper selon le schema
@khyros
Le 1/sqrt(2) est bien logique. Si on fait le calcul en coupant en arc de cercle (et non plus droit) on trouve x=a/sqrt(2) pour tout angle.
ca vient du fait qu'on essaie de séparer une surface (de dimension deux) par un trait (de dimension 1)
c'est donc de l'ordre du m² (metre carré) contre l'ordre du m.
On retombe tres souvent en physique sur quelque chose de proportionnel au carré pour ce genre de calcul. ca ne me choque pas.
#15 - 28-06-2010 11:04:48
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Pizza was ; la dernière part de pizza a partager ...
Merci pour ton indulgence sur l'erreur 
A propos des limites en 0 et pi: la limite en 0 a√(2) me semble finalement logique. Lorsque θ tend vers 0, le problème devient équivalent à partager un triangle isocèle (on néglige la croute).
Pour la limite en pi, le problème ne se pose en fait pas car le partage devient impossible bien avant qu'on atteigne l'angle pi. En effet la part de croute devient trop grosse pour que la partie pointue, même prise en totalité, puisse représenter la même surface. pi est donc en dehors de l'espace de définition du problème.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







