|
#1 - 11-09-2010 12:25:40
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#2 - 11-09-2010 12:51:50
- emmaenne
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3073
- Lieu: Au sud du Nord
Echeecs 6
pourquoi n'utilises-tu pas simplement un rouleau et de la peinture blanche?
Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne)
#3 - 11-09-2010 21:45:28
- Abouri
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 7
Echesc 6
Bonsoir,
Est-ce que l'on peut superposer les "L" ?
Une partie de l'un posée sur l'autre.
Merci pour toute réponse.
#4 - 12-09-2010 01:55:36
- Abouri
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 7
Echeccs 6
Solutionné en moins de 20 minutes en 3 essais décalés dans le temps puisque je travaille sur quelque chose d'autre en même temps.
Comme je suis nouveau, je ne sais pas comment cela se passe pour envoyer la solution.
J'ai peint les "L" en vert pour plus de commodité.
En fait, le problème n'est pas compliqué.
Il suffisait de créer un carré de 5 sur 5 en ayant en tête 9 cases blanches à ne pas couvrir et comme les 2 sur et les 3 sur 2 blanchissent la nappe, le reste est un problème de symétrie : 1 case blanche au centre du plateau, 3 cases blanches en haut et 3 en bas plus 1 case blanche à gauche et à droite.
Ici se trouve la solution, les L sont colorés en vert et numérotées.
Désolé pour la forme.
http://yfrog.com/f1solut1p
#5 - 12-09-2010 11:08:56
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
Echces 6
Ce n'est pas possible.
Il en faut 5 pour s'occuper de la 1ère ligne, 5 autres pour la 3è, 5 autres pour la 5è, 5 autres pour la 7è et 5 autres pour la 9è.
Tu aurais dû colorier les autres cases... ou acheter des L jaunes.
Celui qui fuit les casse-tête ne vaut pas un clou.
#6 - 12-09-2010 11:42:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
ecgecs 6
Bonne réponse de scrablor 
Vasimolo
#7 - 12-09-2010 12:41:14
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Echces 6
Ce n'est pas possible pour une raison de parité.
je fais comme si j'avais cherché 
http://enigmusique.blogspot.com/
#8 - 12-09-2010 15:46:36
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Echesc 6
The proof of the pudding is in the eating.
#9 - 12-09-2010 19:13:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
ecgecs 6
kosmo et franck ont la bonne intuition mais ...
Vasimolo
#10 - 13-09-2010 12:46:38
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Echhecs 6
Après avoir vainement essayé de placer mes 24 triominos sur l'échiquier, je vais essayer de montrer que ce n'est pas possible  . .
Ayant 24 triominos, il faut donc que j'en mette 17 sur une diagonale jaune et 7 sur une diagonale blanche, pour couvrir mes 41 case jaunes (41 = 17 * 2 + 7).
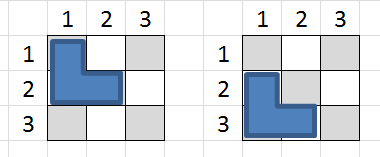
Or, chaque triomino sur 1 diagonale jaune recouvre automatiquement 1 case jaune et une case jaune-rose (voir dessin).
Comme il n'y a que 16 cases jaune-rose, ça n'est pas possible.

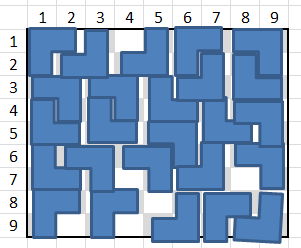
Avec 25 triominos, c'est possible (16 diagonales jaunes et 9 diagonales blanches + 6 cases blanches non recouvertes).
#11 - 13-09-2010 18:00:32
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1972
Echecss 6
J'ai comme l'impression que c'est pas possible, peut-être que je me trompe mais bon.
J'explique: si on analyse l'énoncé et le nombre de cases, on voit qu'on doit avoir 17 L de type "Jaune-Blanc-Jaune" et 7 de type "Blanc-Jaune-Blanc".
De plus, dans un L, on remarque que les deux cases de la même couleur ont un coin en commun.
Autrement dit, peut-on faire des paires de cases jaunes qui se touchent en diagonale, en ayant droit à 7 "jokers"? (un joker est une case jaune libre). Si oui, alors on pourra peut-être répondre au problème et si non, il sera alors impossible d'y répondre.
Considérons maintenant un bord de longueur impaire qui commence et fini par un jaune. Il est impossible de ne pas utiliser de joker sur un tel bord, en effet il y a une case jaune de plus sur le bord que sur la ligne / colonne d'après.
Pour 2 bords, on pourrait penser qu'un seul joker suffit en mettant leur coin commun en joker, mais c'est pas le cas, en effet, il n'y a alors qu'une manière de remplir un bord (toutes les paires "parallèles"), mais on ne peut pas l'appliquer simultanément cette manière au deux bords. Donc pour 2 bords, on utilisera 2 jokers.
On se rend compte de la même manière que pour 3 bords il faudra 3 jokers, et 4 jokers pour 4 bords.
Je commence à remplir mon damier, je peut alors remplir toute la bordure extérieure avec une épaisseur de 2 cases en utilisant 4 jokers sur 7.
Passé cette étape, il me reste quoi ? Un carré 5x5 central vierge. Mince, 5 est aussi un nombre impair, ça veut dire que je vais devoir encore utiliser 4 jokers (vu que ce que je disais est valable pour les cotés de longueur impaire). Ça en fera un de trop (j'avais que 7 jokers à la base)
Voila
#12 - 13-09-2010 23:06:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
echzcs 6
Beaucoup de bonnes réponses mais aucune n'a encore égalé la simplicité de celle de scrabor .
Avis aux amateurs 
Vasimolo
#13 - 14-09-2010 08:38:21
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1972
Echecs
J'ai trouvé mieux que mon précèdent post pour prouver l'impossibilité. On remarque que:
1) On a 4 lignes de 4 cases jaunes et 5 lignes de 5 cases jaunes.
2) Chaque L a cheval sur deux cases jaunes est sur une case jaune d'une ligne de 4 et une case jaune d'une ligne de 5
3) Sur les 24 L, on doit en avoir 17 à cheval sur 2 cases jaunes (34 cases couvertes) et 7 sur une seule case (7 cases couvertes, 7+34 = 41 cases jaunes le compte est bon)
Or, il n'y a que 16 cases jaunes sur les lignes de 4 (d'après 1), donc on peut faire 16 L "Jaune-Blanc-Jaune" au maximum (d'après 2), et il nous en faudrait 17 (d'après 3), donc le problème est impossible à résoudre
#14 - 14-09-2010 16:00:14
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
checs 6
Vasimolo a dit :
On peut faire trourner les "L" mais on ne découpe les pas
Par contre, les mots dans les phrases, on peut découper les et faire les trourner  . .
Bien vu Scrablor  ! !
#15 - 14-09-2010 16:56:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#16 - 14-09-2010 16:59:44
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Echeecs 6
lol^^ je me suis arraché la tete pour trouver, j'ai checrhé en construisant 1 echiqiuer et 24 l blancs, mais j'ai pas trouvé! Mince, pourquoi j'ai pas mis que je pensais qu'il n'y avait pas de solution!!!!! Spoiler : [Afficher le message] [spoiler] [spoiler] Spoiler : [Afficher le message] [spoiler] Lol les 543211 spoilers, ca va marcher, j'espaere ce coup ci! [/spoiler] [/spoiler] [/spoiler]
Un promath- actif dans un forum actif
#17 - 14-09-2010 17:19:29
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
ecgecs 6
Méga lol. Dommage que ça ne fonctionne pas !
#18 - 14-09-2010 19:06:10
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
exhecs 6
http://enigmusique.blogspot.com/
#19 - 14-09-2010 20:40:59
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Echeccs 6
Donc on ne pouvait pas descendre en-dessous de 25 ?
J'ai failli le mettre en réponse, et puis je me suis dit "nooooon, je dois me planter, passer à côté d'une astuce", et du coup je me suis tu  Quel c** je suis ! Quel c** je suis !
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#20 - 14-09-2010 23:01:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Echhecs 6
Pour ta défense la question était un peu piégée 
J'ai eu peur de faire fuir la clientèle en demandant de prouver que c'était impossible . Sûrement ma paranoïa qui reprend le dessus 
Vasimolo
#21 - 15-09-2010 06:30:56
- emmaenne
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3073
- Lieu: Au sud du Nord
Ehecs 6
Moi je me suis dit qu'une fois de plus je ne trouvais pas. 
Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne)
#22 - 15-09-2010 08:50:06
- Flying_pyros
- Sage de Prise2Tete
- Enigmes résolues : 48
- Messages : 3418
- Lieu: Près de la mer
echexs 6
Pareil pour moi... J'avais la solution à 25 mais comme je ne trouvais pas mieux, je me suis dit : "T'es encore à la rue sur ce coup là, passe ton chemin..." 
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum