Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 25-09-2010 09:14:17
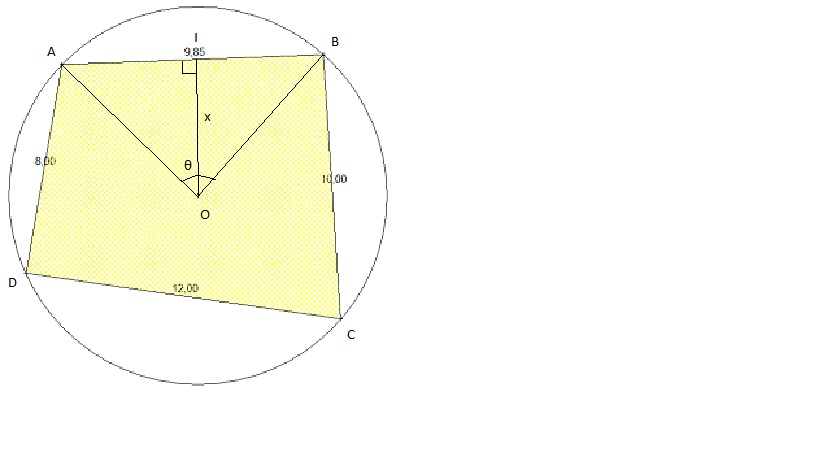
Les mega-terrestresCa y est, je suis dans leur base! Voici un vaisseau alien. Le poste de commande se trouve au dessus du 9,85. Quelle est l'aire de la surface se trouvant au dessus du 9,85? Un promath- actif dans un forum actif
#0 Pub#2 - 30-12-2012 11:25:12
LLes mega-terrestres 3Petit déterrage de topic #3 - 30-12-2012 12:47:05
les mega-terrzstres 3Peut-être que le problème n'avait pas grand intérêt #4 - 30-12-2012 13:36:50
Les mega-terrestres 33J'ai retrouvé ma solution à cette énigme, je l'avais faites mais la réponse était fausse j'avais trouvé 3.256... "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #5 - 30-12-2012 14:05:20
les mega-terrzstres 3Voilà ce que j'ai trouvé: Réponse rapideSujets similaires
|
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.