 |
#1 - 14-11-2010 12:43:30
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
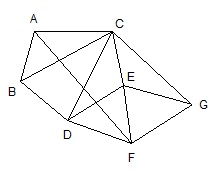
edf ça se compliqur ( + bonus )
#2 - 14-11-2010 12:49:36
- medihv
- Professionnel de Prise2Tete
- Enigmes résolues : 47
- Messages : 123
edf ça se complique ( + bonis )
2 coups nous suffit:
D'abord on touche soit au G soit au F pour éteindre EFG et ensuite on touche au B pour éteindre les 4 autres 
Quand au second problème, je pense que si on laisse les ampoules telles quelles et que on relie B et E je pense que cela serait impossible de tout éteindre (je ne suis pas non plus très sur, la flemme de vérifier  ) )
#3 - 14-11-2010 13:01:14
edf ça se compliqye ( + bonus )
Bonjour,
E puis A. C'est si simple que je ne dois pas avoir compris...
#4 - 14-11-2010 13:30:03
EDF ça se complique (( + Bonus )
Heu... Je vais arrêter la limonade ! Sur le schéma que j'ai vu, A n'était relié qu'à B ; maintenant, il est aussi relié à C...
Du coup, outre que ma réponse est évidemment fausse, l'énoncé "Si j'appuie sur l'interrupteur C je change l'état des ampoules BCDE" le devient aussi puisque A devrait alors changer d'état.
J'aimerais bien être qu'on m'éclaire...
#5 - 14-11-2010 14:46:26
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
EFD ça se complique ( + Bonus )
Coupe le jus au compteur directement ! 
Sinon, je pense que ce qui était valable sur le problème de Yanneck l'est aussi ici (on fait des systèmes d'équation XOR et on résout ce système)
Dans ton exemple, ça donne
A XOR B XOR C = 1
B XOR A XOR C XOR D = 1
C XOR A XOR B XOR D XOR E = 1
D XOR B XOR C XOR E = 1
E XOR C XOR D XOR F XOR G = 1
F XOR E XOR G = 1
G XOR E XOR F = 1
=> D = 0
=> E = 0
=> B XOR C = 1 => A =0
=> F XOR G = 1 => C = 0 => B =1
Conclusion, on appuie sur B et sur F ou G au choix.
#6 - 14-11-2010 15:38:42
- engine
- Professionnel de Prise2Tete
- Enigmes résolues : 37
- Messages : 351
EDF ça se compique ( + Bonus )
Quand c'était une entreprise nationale, il ne s'amusait à faire toutes ces choses embirlificotées.
plouf
#7 - 14-11-2010 16:41:43
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
EDF ça se compique ( + Bonus )
je donne la valeur suivante aux interrupteurs:
On note immédiatement B+F ou B+G=1 1 1 1 1 1 1 c'est a dire qu'ils éteignent toutes les lampes.
aussi
F=G
C+D = A
D+E+F=B
A+B+E+F=C
A+B=D
B+C=E
F et G ne sont pas commandables individuellement
Edit: subsidiairement,
Si on supprime le lien B à D, il n'y a plus rien qui va...
The proof of the pudding is in the eating.
#8 - 14-11-2010 16:53:12
EDF ça se comlpique ( + Bonus )
Quatre propositions :
- B, F
- B, G
- F, B
- G, B
Même commentaire que mon premier...
#9 - 14-11-2010 17:50:02
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 609
EDF ça se commplique ( + Bonus )
#10 - 14-11-2010 18:52:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
EDF ça se compliqu ( + Bonus )
Bonnes réponses de Medihv , RL ( qui râle ) , Scarta , Franck et Gabriel 
Le bonus est très difficile 
Vasimolo
#11 - 14-11-2010 19:12:49
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
edf ça se complique ( + binus )
Je ne vois pas de logique "simple" pour la question normale, par contre j'ai vite eu une idée pour la question bonus : on installe les sept ampoules en cercle. Ainsi, si elles sont initialement toutes allumées, alors on aura toujours un nombre impair d'ampoules allumées 
EDIT : zut, trois ampoules à la fois et non deux (l'ampoule elle-même sera concernée quand on appuie sur son inter). Bon, ça m'apprendra à parler trop vite 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#12 - 14-11-2010 22:47:44
- Flying_pyros
- Sage de Prise2Tete
- Enigmes résolues : 48
- Messages : 3418
- Lieu: Près de la mer
edf çz se complique ( + bonus )
Je dirais BF ou BG pour tout éteindre.
Pour la question bonus, je tente ceci :
Par contre, comment être sur qu'on ne pourra pas tout éteindre après 5, 10 ou 15 manip', aucune idée... 
#13 - 14-11-2010 22:49:30
- supercab
- Habitué de Prise2Tete
- Enigmes résolues : 43
- Messages : 20
EDF ça se compliquee ( + Bonus )
Pour éteindre les lumière on appuie sur B (extinction de A,B,C et D) et F (extinction de E,F et G).
Sauf si l'interrupteur G est plus près que le F, dans ce cas on appuie sur B et G 
Je vais essayer de réfléchir au bonus, mais pour l'instant rien de concluant...
#14 - 15-11-2010 09:07:58
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
edf ça se complique ( + bonuq )
Si j'ai bien compris le bonus, ca revient à montrer que ce sous ensemble de l'ensemble des d'expressions logiques est "SAT-solvable", ou de donner un contre exemple sinon?
Euh...
#15 - 15-11-2010 11:47:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
EDF ça se comlpique ( + Bonus )
Flying_pyros propose sans conviction le contre-exemple suivant :

Alors peut-on tout éteindre ?
Vasimolo
#16 - 15-11-2010 12:25:24
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
EDF ça se complique ( + Bonu s)
Oui, en appuyant sur A, B C, E et G
#17 - 15-11-2010 12:31:35
EDF ça e complique ( + Bonus )
Pour le bonus, je propose un arbre de Steiner à quatre points.
PS : RL = LR = Le Râleur :o)
#18 - 15-11-2010 13:51:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
EDF ça se ccomplique ( + Bonus )
Juste un petit message à RL .
Comme tu as un statut de visiteur , je ne peux pas te répondre par MP ce que j'aurais fait instantanément sinon , j'ai modifié mon dessin initial sans en faire mystère . En l'état je ne peux donc que constater que tu râles sans trop en comprendre l'intérêt .
Je n'ai pas non plus compris ton contre-exemple mais je peux t'assurer qu'il est faux 
Vasimolo
#19 - 15-11-2010 14:14:13
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
EDF ça se compliqu e( + Bonus )
Pour le premier probleme, il s'uffit d'appuyer sur C F et G.
pour le 2eme probleme, je ne pense pas que l'on puisse tout eteindre dans la configuration de Flying_pyros.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#20 - 15-11-2010 15:05:13
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
EDF ça se complique ( ++ Bonus )
J'ai écrit un bout de code qui ressemble à ça grossièrement
J'en suis à n=10 (c'est lent), mais toujours pas de contre exemple, je vais finir par croire que c'est impossible...
Edit: et en plus j'avais un bug.... Bon ben c'est reparti !
#21 - 15-11-2010 16:57:43
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
edf ça se complique ( + binus )
B et F ou B et G me semblent bon
je suis parti en cherchant des interrupteurs situes a 3 liens les uns des autres quels que soient les liens par lesquels on passe. avec les symmetries que comporte le dessin, seul B convient, et le reste se deduit ensuite.
un pentagone ou chaque sommet est relie a tout le monde sauf son n+2, ca marche ?
#22 - 15-11-2010 16:58:58
EDF ça s complique ( + Bonus )
Je crois que j'ai proposé un arbre de Steiner à quatre points, alors que je cogitais sur un arbre à six points. De toute façon, ça ne marche pas : j'ai trouvé comment faire.
J'ai essayé de construire une table booléenne mais ça devient rapidement délirant. N'ayant pas les compétences pour le démontrer, je conjecture donc qu'on peut toujours arriver à tout éteindre en un nombre fini d'opérations, quels que soient la parité des points et le nombre de noeuds.
Donc, pas de contre-exemple. C'est vraiment râlant...
PS : me voir affublé du sobriquet sympathique de râleur m'a amusé et j'avais envie de l'associer à mon pseudo, fût-ce par auto-dérision. Mais je ne râle pas tant que ça, si ?
#23 - 15-11-2010 17:20:21
- Yannek
- Passionné de Prise2Tete
- Enigmes résolues : 10
- Messages : 60
EDF ç se complique ( + Bonus )
Pour l'algorithme, je réfléchis.
Pour le bonus, si l'on a n pièces :
Le problème revient à résoudre l'équation matricielle AX=Y dans Z/2Z où A est la matrice du graphe, Y est le vecteur de (Z/2Z)^n dont tous les coefficients valent 1. et X un vecteur inconnu de (Z/2Z)^n.
(1) On remarque que A est symétrique (matrice d'un graphe non orienté) et que ses coefficients diagonaux valent 1. (chaque chaque interrupteur agit au moins sur la lampe de la pièce où il se trouve)
(2) Le système a des solutions si et seulement si toute combinaison linéaire des lignes dont le premier membre est nul a son second membre nul également.
On remarque que dans notre cas une combinaison de lignes s'écrit :
Li1+...+Likk∈1,...,n,1≤i1<i2<...<ik≤n
En effet le seul coeff non nul disponible dans Z/2Z est 1...
(3) Le second membre d'une combinaison paire (k pair) de lignes est toujours nul (k=2m=0 dans Z/2Z). Donc une combinaison paire de ligne dont le premier membre est nul n'apporte aucune restriction.
(4) Montrons que le premier membre d'une combinaison impaire (k impair) de lignes est nécessairement non nul.
On note
I={i1,...,ik}
l'ensemble des numéros de lignes que l'on ajoute.
Formont A' la matrice carrée extraite de A dont les entrées sont définies par IxI :
A′=(ai1,i1ai1,i2...ai1,ikai2,i1ai2,i2...ai2,ik............aik,i1aik,i2...aik,ik)
Soit en tenant compte de la symétrie de A :
A′=(1ai1,i2...ai1,ikai1,i21...ai2,ik......1...ai1,ikai2,ik...1)
La matrice A' est donc aussi symétrique avec des 1 sur sa diagonale. Ainsi :
∑i,j∈Iaij=∑i,j∈I,i<jaij+∑i∈Iaii+∑i,j∈I,i>jaij=2∑i,j∈I,i<jaij+∑i∈I1=0+k=1
car k est impair. Les sommes des coefficients des colonnes ne peuvent être toutes nulles (sinon la somme de tous les coefficients serait nul) : le premier membre d'un nombre impair de combinaison linéaires n'est jamais nul.
(5) En conclusion, les seules combinaisons de lignes qui mènent à un premier membre nul sont paires et ont un second membre nul, ainsi le système admet toujours des solutions.
Il est toujours possibles d'éteindre toutes les lampes
Joli !
#24 - 15-11-2010 18:59:14
- Bamby2
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 152
edf ça sz complique ( + bonus )
B+FouG...
pour le contre exemple je suis d'accord ca ne marche pas (par résolution, si mon modèle est bon... il n'y a pas de solution).
je continue de chercher !
#25 - 16-11-2010 16:54:54
- laurence03
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 1
EFD ça se complique ( + Bonus )
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








