D'instinct, je verrais un rectangle. Donc 4sinx(1+cosx) dans sa valeur maximum, mais je ne sais pas dériver ça.

Bon alors je vais tenter de préciser à l'instinct.

De mémoire (f.g)'=fg'+f'g
De wiki :  sin'=cos  cos'=-sin

[ 4sinx (1+cosx) ]' = 4 cosx ^2 + 4 cosx - 4 sinx ^2
= 8 cox^2 x + 4 cos x -4

8x^2 + 4x -4 = 0 ? donc cos x = 1/2 ou cos x =-1

cosx = -1 nous donne un carré de surface 0 (le minimum ?)
cosx = 1/2 donc sinx = rac3 /2 donne un rectangle de surface  5,196... ?

Bien vu, Vasimolo!
Bonnes réponses incomplètes de Nombrilist et gwen27

Je pense que l'aire maximale obtenue vaut 4, avec soit un carré de côté 2, ou un rectangle de côtés [latex]2[/latex] et [latex]2\sqrt2[/latex].
Je me lance dans une démo analytique, on verra bien ...

J'ai bien fait de poser quelques calculs ...

Je pars du principe que notre quadrilatère est un rectangle, ayant pour axes de symétrie les tangentes communes aux cercles et passant par le point de tangence.
Ces axes de symétrie forment un repère.
Dans ce repère, le sommet haut droit du rectangle a pour coordonnées :
[TeX]x=1+\cos(\theta)
y=\sin(\theta)[/TeX]
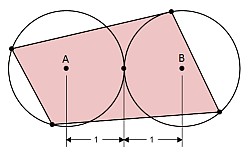
avec \theta entre [latex]0[/latex] et [latex]\frac{\pi}4[/latex]
Il s'agit alors de maximiser xy. En effet l'aire du rectangle vaut 4xy

Je pose [latex]f(\theta)=(1+\cos(\theta))\sin(\theta)[/latex]

Je dérive f pour trouver ses extrama :
[TeX]f'(\theta)=2\cos^2(\theta)+\cos(\theta)-1[/TeX]
Cette fonction s'annule pour 2 valeurs de [latex]\cos(\theta)[/latex] : [latex]\frac12[/latex] et [latex]-1[/latex]
[TeX]-1[/latex] correspond à un minimum, [latex]\frac12[/latex] un maximum.

[latex]\cos(\theta)=\frac12[/latex] lorsque [latex]\theta=\frac{\pi}3[/TeX][TeX]f(\frac{\pi}3)=\frac{3\sqrt3}4[/TeX]
J'en déduis que l'aire maximale pour ce genre de configuration vaut : [latex]\fbox{3\sqrt3}[/latex]

Il ne me reste plus qu'à montrer que c'est cette configuration symétrique qui apporte l'aire la plus grande...
Je ne serai pas étonné que Steiner intervienne dans ce problème ...

Bonnes réponses supplémentaires de franck9525, L00ping007 et halloduda.

gwen27 : une petite erreur dans le deuxième terme de ta dérivée.

looozer a écrit:

On tient le même raisonnement avec la diagonale [NP] et le quadrilatère est alors obligatoirement un rectangle dont la diagonale vaut deux fois la largeur avec l'angle MAN valant 120°.

je voudrait dire que contrairement à ce qui est écrit je n'y suis pour rien