EDIT suite à complément d'énoncé

Pour un gâteau 3x4 = 12 parts, les résultats sont :



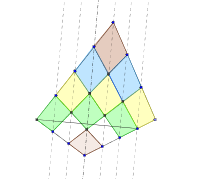
2 familles de 2 et 2 familles de 3 personnes

1 part   100 soit 100 g pour Vasimolo     brun
2 parts 120 soit 240 g pour famille 1 de 2 personnes bleu
3 parts 140 soit 420 g pour famille 2 de 3 personnes jaune
3 parts 160 soit 480 g pour famille 3 de 3 personnes vert
2 parts 180 soit 360 g pour famille 4 de 2 personnes blanc
1 part   200 soit 200 g pour le pâtissier  rose

Total                  1800 g

C'est une possibilité Halloduda

Est-ce la seule et pourquoi ????

Vasimolo

C'est la seule répartition 3x4 que j'aie pu trouver.

Pour le principe, gâteau nxm, ce n'est pas la seule, on peut construire une répartition nxn pour n quelconque. Vérification Geogebra faite pour 5x5.
La progression arithmétique est alors 8, 9, 10, ..., 16.

Pour nxm on en prend un sous-ensemble de nxn en corrigeant le rapport (2 pour nxn).
Il me semble que pour tout n les diagonales (perpendiculaires) du gâteau nxn sont dans le rapport 3/2. Ça ressemble à un cerf-volant.

Je ne sais pas le démontrer.
Je ne sais pas non plus démontrer les spoilers.

Merci Halloduda pour la participation et la réponse

Vasimolo

Une explication pour le premier indice

On considère un quadrilatère [latex]ABCD[/latex] et des points [latex]E,F,G[/latex] et [latex]H[/latex] sur les côtés
[TeX][AB],[BC],[CD][/latex] et [latex][DA][/latex] tels que [latex]\frac{EB}{EA}=\frac{GC}{GD}=p[/latex] et [latex]\frac{FC}{FB}=\frac{HD}{HA}=q[/latex] .

Il faut montrer qu’alors [latex]\frac{OF}{OH}=p[/latex] et [latex]\frac{OG}{OE}=q .[/TeX]
On trace les parallèles à [latex](HF)[/latex] passant par [latex]B,C,E,G .[/latex]

Comme [latex]\frac{HD}{HA}=q , d=fq[/latex] et alors [latex]\frac{OG}{OE}=q[/latex] . De même [latex]\frac{OF}{OH}=p[/latex] .

On en déduit aisément que les différentes coupes du gâteau sont partagées en parts égales .

A suivre ...

Vasimolo

J'aimerai bien répondre à l'énigme mais je ne comprends pas ça :

Il partage les côtés en parts égales avant de trancher en ligne droite. Comme deux parts se sentent un peu seules , il prend la plus grosse et me confie l'autre, deux fois plus petite.

Enfin je ne vois pas le rapport, n'y ce que ça représente par rapport à ton schéma...

Shadock

Oui merci c'est déjà beaucoup plus clair, bon il n'y a plus qu'à réfléchir

En fait la partie géométrique de l'énigme est complètement évacuée par les deux indices .

Il reste à prouver l'unicité de la solution

Pour résumer le problème :

On a une grille 3X4 dont la somme des cases est 1800 et telle que chaque ligne et chaque colonne est en progression arithmétique . Si on regroupe les cases de même valeur , seules deux cases restent isolées et la plus grande des deux vaut deux fois la plus petite .

Je précise que je n'ai aucune solution simple même si je suis quasi convaincu de l'unicité de la solution .

Ainsi résumé le problème peut intéresser ceux qui ont un goût modéré pour les gâteaux et la géométrie

Vasimolo

@Shadock

Je te rassure la plupart de mes rêves ne parlent pas de maths et j'ai une vie sociale et familiale plutôt équilibrée

Comme la plupart des habitués du site je comble mes temps morts en imaginant de nouveaux instruments de torture ou en m'essayant à ceux des autres

C'est sûrement ridicule mais ces problèmes font partie de mes détentes favorites .

Vasimolo

PS : Sinon au point où on est rendu je suis presque sûr que le problème a une solution évidente .

Bon réveillon !!!

Salut, j'ai trouvé également une démonstration de l'unicité :

Si l'on note la grille :

i, j, k, l
e, f, g, h
a, b, c, d

Alors, pour ne pas avoir de part isolée à part a et l, il faut b=e et k=h.

en notant b=a+r et f=a+r+s, on obtient alors :

a+2r, a+r+2s,   a+4s, a-r+6s
 a+r,  a+r+s, a+r+2s, a+r+3s
   a,    a+r,   a+2r,   a+3r

k=h donne a+4s=a+r+3s donc r=s, ce qui donne :

a+2r, a+3r, a+4r, a+5r
 a+r, a+2r, a+3r, a+4r
   a,  a+r, a+2r, a+3r

De 2a=l, on en déduit que a=5r.
Puis en utilisant que la somme fait 1800, on trouve que a=100 et r=20.

Aux symétries près les possibilités sont résumées sur les graphiques suivants 





Un seul réalise une progression arithmétique sur les ordonnées , il correspond aux calculs de Titou .

Vasimolo

En effet c'est bien plus rapide comme ça

On peut remarquer que s'il y a plusieurs petites parts ou plusieurs grandes parts , les coupes dans une des deux directions sont parallèles et alors les parts dans chaque bande sont toutes égales , ce qui contredit l'hypothèse .

Il n'était pas si difficile ce gâteau .

Vasimolo