Il faut et il suffit qu'aucun morceau ne mesure plus d'un demi-bâton.
donc
Il faut et il suffit que la 2ème marque soit à moins d'un demi-bâton de la 1ère, mais dans l'autre moitié du bâton. Cette probabilité vaut :
[TeX]2 \int_{0}^{1/2} x ~\textrm{d}x = \frac{1}{4}[/TeX]

OK je viens de piger. Soit a, b et c la taille des 3 morceaux et t la taille du bâton. Pour pouvoir construire un triangle, il faut que:

c=<a+b
b=<a+c
a=<b+c

Comme a+b+c = t il vient comme condition nécessaire et suffisante pour construire un triangle:

a=<t/2
b=<t/2
c=<t/2

Après, calculer ces probas là sur des variables aléatoires continues... Il faut y aller avec des intégrales ?

@nombrilist : pas forcément (à part peut-être pour la question 1bis).

@titoufred : oui, tu as raison, (je viens de refaire mes calculs ). Pardon.

@masab: Oui !

@titoufred : exact !

@fix33 : Non, par exemple sur un bâton de longueur 1 tu peux avoir la première
coupure à 0,1 et la deuxième coupure à 0,9, tu ne pourras pas faire de triangle et
pourtant les deux coupures sont sur une moitié différente du bâton.

Pour la question 2, j'ai trouvé [latex]p_n = 1 - \frac{n}{2^{n-1}}[/latex]

Est-ce la bonne réponse ?

J'écris mon raisonnement dès que possible.

Question 1 : 1/4. C'est le rapport entre les deux triangles qui "définissent" les nombres l'un par rapport à l'autre.

Question 2 : Au pif, je propose 1/(n+1) ! 1 chance sur 5 d'avoir bon !

Je réfléchis à la question 1 bis ... mais à ce qu'il paraît, il faut utiliser le logarithme népérien (je viens de me le rappeler) et je ne sais même pas ce que c'est ...
Au fait, j'avais posé la question a ma prof et c'est elle qui m'a dit ça.

J'expose ma solution, qui n'est pas la plus simple je présume.
Je ne détaille pas tout, c'est déjà bien assez long. S'il y a des points obscurs, je donnerai des précisions.

Le bâton est assimilé au segment [0 ; 1].
[TeX]n[/latex] désigne un entier supérieur ou égal à 2.
On note [latex]x_1, x_2, ..., x_{n-1}[/latex] les nombres tirés aléatoirement dans [0 ; 1] pour découper le bâton en [latex]n[/latex] morceaux.

Pour pouvoir faire un polygone à [latex]n[/latex] côtés avec les [latex]n[/latex] morceaux de bâton, il faut et il suffit que le plus long de ces morceaux mesure moins de 1/2.

On appelle [latex]p_n[/latex] la probabilité de pouvoir faire un polygone à [latex]n[/latex] côtés avec un bâton coupé aléatoirement en [latex]n[/latex] morceaux,
[latex]X_n[/latex] la variable aléatoire correspondant à la longueur du plus grand des [latex]n[/latex] morceaux,
[latex]Y_n = 1-X_n[/latex] la variable aléatoire correspondant à la longueur restante du bâton,
[latex]f_n[/latex] la densité de probabilité de la variable aléatoire [latex]Y_n[/latex].

Nous allons chercher à établir la formule de la densité [latex]f_n[/latex], uniquement sur l'intervalle [0 ; 1/2].
Pour toute la suite, on considère [latex]0<x<1/2[/latex].

[latex]f_2(x)dx=P(x<Y_2<x+dx)=P(x<x_1<x+dx)+P(1-x-dx<x_1<1-x)[/TeX][TeX]f_2(x)dx=dx + dx = 2dx[/latex] et donc [latex]f_2(x)=2[/TeX]
Nous allons maintenant chercher une relation de récurrence sur les [latex]f_n[/latex].
[TeX]f_{n+1}(x)dx = P(x<Y_{n+1}<x+dx)[/TeX][TeX]f_{n+1}(x)dx = P(x<Y_{n+1}<x+dx \cap Y_{n+1}=Y_n) + P(x<Y_{n+1}<x+dx \cap Y_{n+1}>Y_n)[/latex]  (1)

On suppose que l'on a déjà virtuellement cassé le bâton en [latex]n[/latex] morceaux, et que le plus long de ces morceaux mesure plus de 1/2.
Ce plus long morceau a pour extrémités des points(nombres) [latex]a[/latex] et [latex]b[/latex] et sa longueur vaut [latex]X_n = b-a[/latex]. La longueur restante du bâton est [latex]Y_n=1+a-b[/latex]. Remarquons que [latex]X_n >1/2[/latex] et donc [latex]Y_n <1/2[/latex].

Pour créer le [latex](n+1)^{ème}[/latex] morceau, on va tirer aléatoirement un [latex]n^{ème}[/latex] point noté [latex]x_n[/latex] dans [0 ; 1].

Le morceau le plus long ne va pas diminuer de longueur lorsque [latex]x_n[/latex] est tiré à l'extérieur de ce morceau, ce qui arrive avec une probabilité de [latex]Y_n[/latex].

Une fois que [latex]Y_n[/latex] est fixé, alors [latex]P(Y_{n+1}=Y_n) = Y_n[/latex]. Et donc :

[latex]P(x<Y_{n+1}<x+dx \cap Y_{n+1}=Y_n) = P(x<Y_n<x+dx) P(Y_{n+1}=Y_n)[/TeX][TeX]P(x<Y_{n+1}<x+dx \cap Y_{n+1}=Y_n) = f_n(x)dx \times x =  xf_n(x)dx[/latex]  (2)

Le morceau le plus long va diminuer tout en restant supérieur à 1/2 dans deux cas bien distincts :
lorsque [latex]a<x_n<b-1/2[/latex] ou lorsque [latex]a+1/2<x_n<b[/TeX][TeX]Y_n[/latex] étant fixé, pour [latex]x[/latex] tel que [latex]Y_n<x<1/2[/latex], on obtient :

[latex]P(x<Y_{n+1}<x+dx) = P(a+x-Y_n<x_n<a+x-Y_n+dx) + P(b+Y_n-x-dx<x_n<b+Y_n-x)[/TeX]
et donc [latex]P(x<Y_{n+1}<x+dx) = 2dx[/latex]

Ainsi :
[TeX]P(x<Y_{n+1}<x+dx \cap Y_{n+1}>Y_n) = P(0<Y_n<x)P(x<Y_{n+1}<x+dx)[/TeX][TeX]P(x<Y_{n+1}<x+dx \cap Y_{n+1}>Y_n) = \int_{0}^{x} f_n(t) ~\textrm{d}t  2dx[/latex]  (3)

Finalement, de (1), (2) et (3), on tire que :

[latex]f_{n+1}(x)dx = xf_n(x)dx + \int_{0}^{x} f_n(t) ~\textrm{d}t ~2dx[/TeX]
Ou plus simplement, on obtient la relation de récurrence suivante :
[TeX]f_{n+1}(x) = x f_n(x) + \int_{0}^{x} 2 f_n(t) ~\textrm{d}t[/latex]  (4)

On prouve alors par récurrence que :

[latex]f_n(x) = n(n-1)x^{n-2}[/latex]  (5)

Démonstration de l'hérédité :

[latex]f_{n+1}(x) = x f_n(x) + \int_{0}^{x} 2 f_n(t) ~\textrm{d}t = n(n-1)x^{n-1} + \int_{0}^{x} 2n(n-1)t^{n-2} ~\textrm{d}t[/TeX]
donc [latex]f_{n+1}(x) = n(n-1)x^{n-1} + 2nx^{n-1} = n(n+1)x^{n-1}[/latex]

Ce qui prouve l'hérédité.

Finalement,
[TeX]p_n= 1- \int_{0}^{1/2} f_n(x) ~\textrm{d}x =1- \int_{0}^{1/2} n(n-1)x^{n-2} ~\textrm{d}x=1-[nx^{n-1}]_0^{1/2} = 1-\frac{n}{2^{n-1}}[/TeX]

Pour la Q1:Après un raisonnement logique je trouve 25%.
Pour les autres questions c'est titou qui joue.

D'abord merci, pour vos participations.

Pour ce problème, on peut modéliser le bâton par le segment [latex][0;1][/latex]
Les endroits où l'on coupe le bâton sont des nombres tirés aléatoirement entre 0 et 1.

On peut faire un triangle (ou un polygone) ssi tous les morceaux sont plus petits que 1/2.

Question 1 :

Pour le triangle, on tire deux nombre aux hasard entre 0 et 1.
On peut représenter le premier nombre sur un axe des abscisses, et l'autre sur un axe des ordonnées.
Ensuite on peut déterminer les régions qui sont des cas favorables ou défavorables, on obtient la figure suivante :



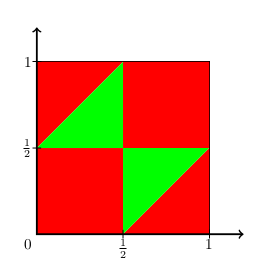
Les cas défavorables sont en rouges et les cas favorables en verts. Par exemple, si un point se trouve dans le carré rouge en bas à gauche, alors cela signifie que les deux coupure sont dans le segment  [latex][0;{1\over 2}][/latex]  , donc nous avons un morceau plus grand que 1/2 on ne peut donc pas faire de triangle.

Le rapport des cas favorables (les triangles vert) sur les cas possible (carré de coté 1) est de 1/4.
On a donc 1/4 d'avoir un triangle.

Question 1bis :

Soit [latex]x[/latex] le premier tirage. Supposons [latex]x<{1\over 2}[/latex] .
Nous avons donc un petit bâton de longueur [latex]x[/latex], et un grand bâton de longueur  [latex]1 - x[/latex]. Pour pouvoir faire un triangle il faut que le plus grand bâton soit choisit, et ce bâton à 1/2 d'être choisit.

Pour pouvoir faire un triangle, il faut que le deuxième tirage soit dans l’intervalle  [latex][{1\over 2};x+{1\over 2}][/latex]  (sinon on aurait un morceau plus grand que 1/2).
Cet intervalle est de longueur [latex]x[/latex], et la probabilité d'être dans un intervalle de longueur [latex]x[/latex] sur un bâton de longueur  [latex]1-x[/latex]  est  [latex]{x\over {1-x}[/latex].
Donc en faisant varié [latex]x[/latex] entre 0 et 1/2 on a la probabilité d'avoir un triangle qui est:
[TeX]{1\over 2} \int_0^{1\over 2}{x \over {1 - x}}\hbox{ d}x [/TeX]
Et nous avons la même probabilité pour [latex]x[/latex] variants entre 1/2 et 1. Donc la probabilité finale d'avoir un triangle est :
[TeX]\int_0^{1\over 2}{x \over {1 - x}}\hbox{ d}x = \ln(2) - {1\over 2} [/TeX]
Question 2 :

Faisons [latex]n-1[/latex] marque aléatoirement sur le bâton.
Ensuite posons  [latex]x_0 = 0[/latex] , [latex]x_n = 1[/latex] , et notons [latex]x_1,\ldots, x_{n-1}[/latex] les [latex]n-1[/latex] marques dans l'ordre croissant.

Nous avons donc [latex][x_i;x_{i+1}][/latex] qui représente le (i+1)-ème morceau.

Calculons la probabilité de pas obtenir de polygone :

Soit [latex]p[/latex] cette probabilité.
On ne peut pas obtenir de polygone ssi il existe un morceau plus grand que 1/2.
Notons  [latex]E_i[/latex] l’événement  [latex][x_i;x_{i+1}] > {1\over 2}[/latex]  (c'est un abus de notation pour dire que la longueur de l'intervalle [latex][x_i;x_{i+1}][/latex] est plus grande que 1/2.

La probabilité de ne pas avoir de polygone est donc égal à la probabilité que
l'un des événements E_i soit réalisé c'est-à-dire :
[TeX]p = P(\bigcup_{i=0}^{n-1} E_i)[/TeX]
Or les événements [latex]E_i[/latex] sont disjoints (en effet, il est impossible d'avoir deux morceaux plus grand que 1/2), nous avons donc :
[TeX]p = \sum_{i=0}^{n-1} P(E_i)[/TeX][TeX]P(E_i)[/latex] représente la probabilité que le (i+1)-ème morceaux soit plus grand que 1/2.

En supposant que l'on ait un morceau plus grand que 1/2, comme les [latex]x_i[/latex] ont été tirés uniformément, tous les morceaux ont chacun une chance équiprobable d'être celui qui est plus grand que 1/2.  Cela signifie que [latex]P(E_i)[/latex] ne dépend pas de [latex]i[/latex]. Car si pour [latex]i\ne j[/latex] nous avons :
 
  [latex]P(E_i)=a[/TeX]
[TeX]P(E_j)=b[/TeX]
Si a < b alors comme l'événement E_j est plus probable que l'événement E_i,
alors le {j+1}-ème morceau aura plus de chance d'être le morceau plus grand
que 1/2 que le morceau (i+1). Nous avons donc a = b (car on a un raisonnement symétrique pour a > b).

Et donc :
[TeX]p = \sum_{i=0}^{n-1} P(E_0) = n * P(E_0)[/TeX]
Or [latex]P(E_0)[/latex] est la probabilité que l'intervalle [latex][x0; x_1][/latex]  soit plus grand que 1/2, et cela signifie que les  [latex]n-1[/latex] tirages sont dans le segment [latex][{1\over 2};1][/latex] et cela a [latex]1\over{2^{n-1}}[/latex] d'arrivé.

Ainsi [latex]p = {n\over{2^{n-1}}[/latex]  et donc la probabilité de pouvoir faire un polygone à  [latex]n[/latex] cotés est :

[latex]1 -  {n\over{2^{n-1}}[/latex].

Euh..., non (smiley avec les joue rose)

Cela fait assez longtemps que j'ai vu ce problème, et cela m'avais assez marqué pour que je me souvienne des grandes lignes, mais cette partie là, je n'ai pas réussi à la retrouvé

Je suis désolé, quand je me suis rappelé cette énigme, je me suis dit que c'était une occasion de poster  une énigme sur Prise2Tete, mais j'aurai du d'abord vérifier que j'avais tous les éléments.

La prochaine fois je ferais attention