 |
#1 - 03-04-2014 19:10:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 03-04-2014 19:14:59
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
gâteay 74
Non, si un côté du triangle est bleu et les deux autres rouges.
Ou alors tu considères q'un côté de l'équerre peut suivre un côté du triangle ?
#3 - 03-04-2014 19:17:24
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâteeau 74
Bonjour. Je n'ai pas compris avec quelle méthode est déterminé l'alternance (bleu et rouge) du périmètre du gâteau. Les tirets bleus et rouges ne semblent pas de même longueur, ni pour tout le périmètre, ni pour chaque côté.
#4 - 03-04-2014 19:25:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 774
Le coloriage du bord est quelconque et les sommets de l’équerre peuvent se confondre avec ceux du gâteaux .
Vasimolo
#5 - 03-04-2014 20:00:30
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
Gâteau 7
Alors, oui, c'est toujours possible car un minuscule bout de rouge issu d'un sommet m'oblige à en colorier un plus gros bout en bleu sur le côté voisin (projection de la hauteur) qui m'oblige lui-même à prolonger mon premier bout rouge...etc.
Résultat, un côté commençant d'une couleur doit être intégralement de cette couleur.
J'aurai deux côtés de même couleur. Conclusion par l'absurde : si je tente de l'empêcher, c'est possible.
#6 - 03-04-2014 20:22:35
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâtea u74
Salut !
Peut-on aussi placer 2 sommets sur un même bord ? Si oui, la démo me semble plus simple...
#7 - 03-04-2014 20:25:17
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
fâteau 74
Les dimensions de l'équerre sont fixées au départ où pas ?
#8 - 03-04-2014 21:36:58
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Gâteau 744
Si je mets un coté en bleu et les deux autres en rouge, ça marche pas, si ?
#9 - 03-04-2014 21:55:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 47
@Gwen : ?
@Golgot : oui .
@Titou : non .
@Godisdead : si .
Vasimolo
PS : deux sommets de l'équerre peuvent partager le même côté .
#10 - 04-04-2014 18:53:37
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâtea 74
Cherchons à empêcher le fait de pouvoir tracer un triangle rectangle inscrit dans le premier et avec 3 sommets de même couleur.
Il suffit de se concentrer sur un des angles du triangle.
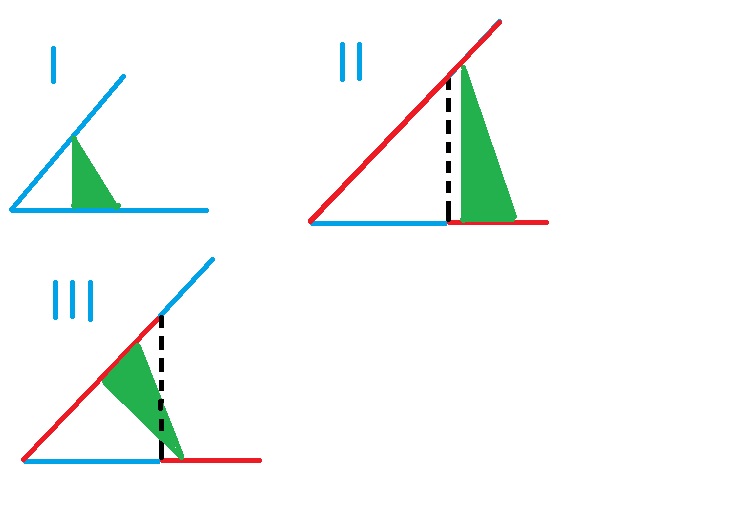
Si le départ de l'angle est de la même couleur sur chaque côté, on peut aisément construire un triangle rectangle inscrit dont les 3 sommets sont de même couleur. Voir figure 1
Sinon, On suppose que le début d'un côté est d'une couleur, bleu dans la figure 2, alors l'autre doit démarrer par du rouge, mais il doit s'arrêter au droit du point où la couleur change sur le 1er côté, au risque de construire de nouveau un triangle rectangle inscrit dont les 3 sommets sont de même couleur.
Enfin, même si on s'arrête "à temps", alors on pourra quand même construire un triangle rectangle inscrit dont les 3 sommets sont de même couleur en s'appuyant cette fois sur le 2ème côté en démarrant juste après le changement de couleur. voir figure 3.
Conclusion : On pourra toujours construire un triangle rectangle inscrit dont les 3 sommets sont de même couleur.
#11 - 04-04-2014 19:09:12
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteaau 74
Salut Vaismolo,
Je suis sûrement obtus car je n'ai pas compris la question...
#12 - 04-04-2014 19:10:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gââteau 74
@Golgot : le coloriage des côtés est fait point par point , on peut par exemple imaginer un coloriage tel que tout segment non réduit à un point contient des points de chaque couleur . La frontière bicolore du gâteau est l'unique hypothèse .
Vasimolo
#13 - 04-04-2014 19:13:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
fâteau 74
@Nodgim : la frontière du triangle est arbitrairement coloriée avec deux couleurs . Peut-on choisir sur cette frontière trois points de même couleur formant un triangle rectangle ?
Vasimolo
#14 - 04-04-2014 19:42:44
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteauu 74
Houuuu ! Ton pâtissier est drôlement minutieux ! 
#15 - 04-04-2014 20:33:17
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,998E+3
Gâtea 74
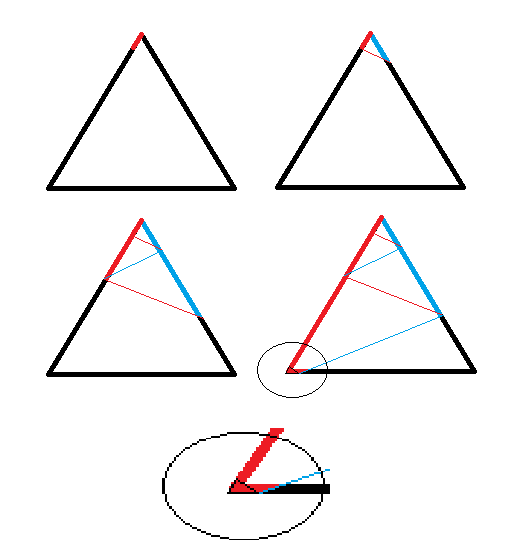
Pour expliquer :
#16 - 04-04-2014 21:06:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteu 74
@Gwen : ton raisonnement serait correct si le coloriage était réalisé en lignes continues mais mon pâtissier est un fervent adepte du pointillisme .
Vasimolo
#17 - 04-04-2014 22:14:59
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Gâtea 74
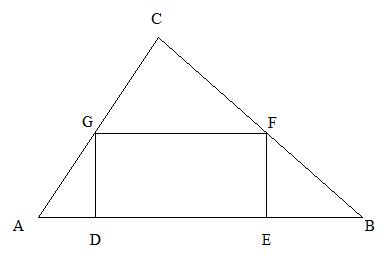
On trace un rectangle DEFG.
Si un des triangles ADG, GDE, GDF ou AEF possède 3 sommets de même couleur, c'est gagné (=on a notre nougatine !).
Sinon, aucun des triplets ci-dessus n'est monochrome.
Supposons D et G sont de même couleur (choisissons bleu sans réduire la généralité du problème), alors A est rouge (pour que AGD soit multicolore), de même G et F. Donc AFE est monochrome rouge : c'est impossible. Donc D et G sont de couleur différente.
On fait courir G entre A et C : soit on tombe à un endroit sur un des 4 triplets monochromes et c'est gagné, soit D et G sont toujours de couleur différente, donc à aucun moment G ou D n'ont les 2 couleurs.
Donc ]AC[ (bornes exclues) est monochrome.
Les 3 cotés jouant des rôles identiques (triangle acutangle), soit on sera tombé sur un triplet monochrome soit on aura chaque coté monochrome. Par exemple 1 rouge et 2 bleus. Il sera alors toujours possible de construire un triangle rectangle prêt du sommet reliant les 2 cotés bleus.
#18 - 04-04-2014 22:42:00
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 4
Supposons qu'il y ait un enchaînement de "a" couleurs sur le côté horizontal du bas.
Alors à leur vertical, si on veut empêcher la création d'un triangle rectangle dont les sommets ont la même couleur, il faut que chaque couleur sur le côté au dessus correspondant (gauche ou droit) soit inversée par rapport à celle d'en dessous (sinon il suffit de relier ces 2 points avec un autre point du segment horizontal de la même couleur). Voir le pas joli dessin.
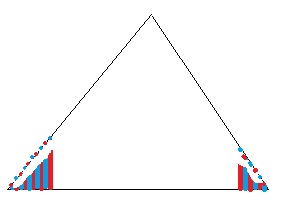
Du coup, le côté gauche + le côté droit contiennent en tout b+c = a couleurs
Avec le même raisonnement, mais en partant des 2 autres côtés, on trouve a+c = b et a+b = c
Donc a=b=c=0 couleur ce qui est impossible !
Conclusion, on peut toujours faire un triangle rectangle avec des sommets de la même couleur et inscrit dans le triangle de base !
#19 - 05-04-2014 09:33:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 7
@Dylasse : je ne vois pas pourquoi G et D devraient garder une couleur constante quand G est mobile sur [AC] .
@Golgot : a , b, et c peuvent être infinis et l'arithmétique des infinis est un peu plus complexe que celle de N .
Vasimolo
#20 - 05-04-2014 09:50:44
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâetau 74
Il suffit d'avoir un coté en bleu et les 2 autres en rouge...
#21 - 05-04-2014 10:29:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâtea 74
Ce n'est pas si simple Nodgim .

Vasimolo
#22 - 05-04-2014 10:56:49
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâeau 74
L'infini, ça me dépasse... 
Tu as trouvé une explication qui n'en dépend pas ?
#23 - 05-04-2014 11:07:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
GGâteau 74
Oui Golgot , il y a une solution simple 
Vasimolo
#24 - 05-04-2014 13:42:31
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Gâteaau 74
A la demande générale (de Vasimolo), je vais expliciter pourquoi aucun point G ne peut être bicolore...
Montrons que si G est bicolore, alors G va nous permettre de construire un triangle monochrome.
G et D sont évidemment de la même couleur (par exemple bleu).
Soit au moins l'un des 3 A, E ou F est bleu et donc un des 3 triplets formés par G,D et A,E ou F est monochrome bleu. Soit A, E et F sont rouges et forment un triangle monochrome.
Donc si G est bicolore, je suis certain de pouvoir construire un triangle rectangle monochrome.
J'en déduis que le segment ]AC[ est monochrome.
On poursuit alors le raisonnement en montrant que l'on arrive à une autre contradiction.
remarque : je fais peut-être un raccourci topologique en considérant que en chaque point X je vais trouver 2 segments ouverts (à droite et à gauche) monochromes (ce qui semble réaliste pour une œuvre pâtissière).
Dis autrement, je considère que si Y et Z sont 2 points de couleurs différentes de ]AC[ alors il y a un point W de [YZ] qui est bicolore.
#25 - 05-04-2014 15:38:29
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
âteau 74
Le projeté orthogonal d'un secteur rouge sur la portion de triangle qui lui fait face doit être bleu, sinon on peut tracer un triangle rectangle.
Cela implique immédiatement que de part et d'autre d'un sommet, on ait alternance de couleur, car les angles sont plus petits que l'angle droit.
Ainsi une portion 1 de bleu depuis un sommet aura comme projeté orthogonal une portion rouge 2 depuis ce sommet. Mais le projeté de cette portion rouge 2 aura elle même un projeté orthogonal bleu 3 plus grand que la portion 1. Et ainsi de suite jusqu'à ce que l'un des projetés empiète sur le 3ème segment, qui devra bien avoir une couleur identique à l'un des sommets déja colorié.
Il est donc impossible d'avoir 3 sommets avec alternance de couleur, et par conséquent on peut tjs tracer un triangle rectangle monochrome.
|
 |

 Accueil
Accueil
 Forum
Forum












