 |
#51 - 12-06-2014 16:36:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#52 - 12-06-2014 19:31:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 778
Dans l'élan et au premier essai :
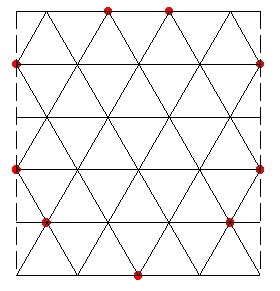
A recouvrir avec deux triangles 6X6 .
On peut conjecturer qu'il existe un ensemble de n points d'un quadrillage triangulaire qu'on ne peut pas recouvrir avec deux triangles équilatéraux de côté n-3 correctement orientés ( sans chevauchement ) mais dont on peut recouvrir toute partie à n-1 éléments .
Vasimolo
PS pour Gwen : j'ai bien vu ta demande pour les neuf points . Je donnerai ma preuve ( on ne fait pas de la magie mais des maths donc on partage ses secrets ) , j'attends simplement de voir si quelqu'un à une idée pourquoi neuf et pas huit ou sept car personnellement je n'en sais rien et qu'apparemment le problème n’intéresse personne . En bref on se débarrasse d'abord du problème des gâteaux sans chevauchement puis on revient au problème initial que je trouve bien plus intéressant 
#53 - 14-06-2014 10:20:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâteay 78
Si on accepte les chevauchements j'ai trouvé un exemple de neuf points qu'on ne peut pas cacher avec deux triangles alors qu'on peut cacher huit quelconques d'entre eux .
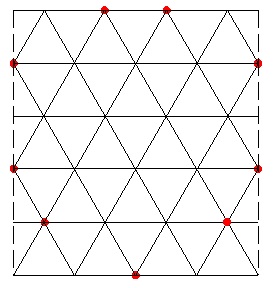
Les gâteaux étant des triangles 5X5 .
Il faut donc pouvoir couvrir au moins neuf taches quelconques pour être assuré de cacher l'ensemble des taches . Le problème initial est bien extrémal , il reste à le démontrer .
Vasimolo
#54 - 15-06-2014 12:36:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtaeu 78
J'avais tellement séparé les problèmes ( avec ou sans superposition ) que je ne me suis même pas rendu compte que j'avais expédié la même image dans les deux derniers messages : un lien caché ?
Vasimolo
#55 - 15-06-2014 19:53:07
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâteau 778
Pour le cas sans chevauchements, voici un exemple 11 points dont on peut toujours recouvrir 10 d'entre eux sans pouvoir tous les recouvrir :
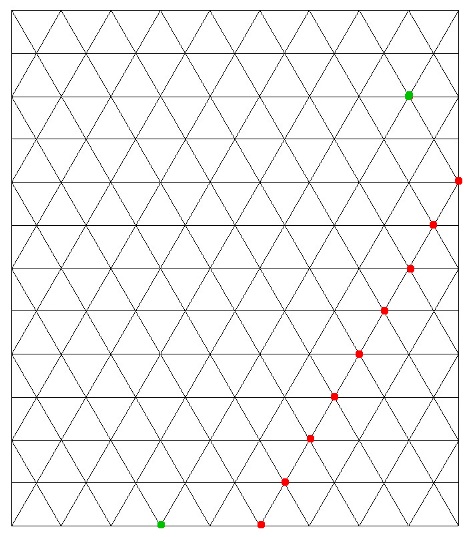
Les gâteaux sont 9 x 9.
De manière générale, sur le même modèle, si on a k points rouges, alors on a k+2 points dont on peut toujours recouvrir k+1 d'entre eux mais pas tous avec des triangles k*k. Je ne détail pas plus, mais je pense qu'on peut facilement s'en convaincre.
Donc effectivement, si le pâtissier ne s'autorise pas les chevauchements alors ce n'est pas certains qu'il puisse recouvrir toutes les taches.
Il y a sûrement plus simple.
#56 - 16-06-2014 10:55:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtaeu 78
Parfait Cogito .
Tous les problèmes sont donc réglés . Il reste seulement à montrer dans le cas des recouvrements autorisés que si on peut cacher 9 taches quelconques avec deux gâteaux , on peut les cachées toutes .
Vasimolo
#57 - 18-06-2014 15:09:39
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâteu 78
Finalement, je reviens sur mon idée de tracer le plus petit triangle équilatéral qui contient tous les points et qui a la même orientation que les gâteaux, je crois que j'ai mal exploité cette idée.
D'abord un résultat préliminaire :
Un gâteau peut recouvrir un ensemble de taches si et seulement si il peut recouvrir trois taches quelconque de cet ensemble de taches. (la démonstration est laissée en exercice  ) )
En particulier cela signifie que si un gâteau ne peut pas recouvrir un ensemble de taches, alors il existe trois tâches de cet ensemble qui ne peuvent être recouverte.
Remarque à propos des résultats précédents : Pour éviter de vous encombrer avec plein de détails, je suppose que mon ensemble de tache à au moins trois taches.
Dans la figure ci-dessous, le plus petit triangle équilatéral contenant tous les points est en violet. On peut toujours se ramener à avoir un des gâteaux dans un angle du triangle violet. Ce qui nous fait donc trois positions possibles pour le gâteau en gris :
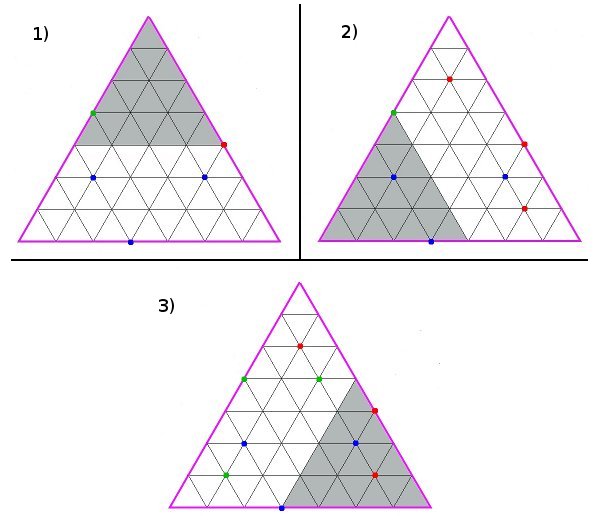
Remarque à propos de l'image :Dans cette image, tous les points ne sont pas représentés. On sait seulement que dans le triangle violet il y a plein de points, j'ai dessiné que quelques points intéressants à titre d'exemple.
-----------
Dans le cas 1) appelons B (comme bleu) l'ensemble des points qui sont dans la zone non grisé du triangle violet.
-Si avec le second gâteau je peux recouvrir trois points quelconques de B alors d'après le résultat préliminaire, je pourrais recouvrir tous les points de B et donc tous les points seront recouvrables par les deux gâteaux.
-Sinon, il existe trois points de B qui ne peuvent pas être recouverts par le second gâteau. Sur le dessin ce sont les trois points bleus.
----------- (aux noms des couleurs près, c'est un copier coller)
Dans le cas 2) appelons R (comme rouge) l'ensemble des points qui sont dans la zone non grisé du triangle violet.
-Si avec le second gâteau je peux recouvrir trois points quelconques de R alors d'après le résultat préliminaire, je pourrais recouvrir tous les points de R et donc tous les points seront recouvrables par les deux gâteaux.
-Sinon, il existe trois points de R qui ne peuvent pas être recouverts par le second gâteau. Sur le dessin ce sont les trois points rouges.
-----------
Dans le cas 3) appelons V (comme vert) l'ensemble des points qui sont dans la zone non grisé du triangle violet.
-Si avec le second gâteau je peux recouvrir trois points quelconques de V alors d'après le résultat préliminaire, je pourrais recouvrir tous les points de V et donc tous les points seront recouvrables par les deux gâteaux.
-Sinon, il existe trois points de V qui ne peuvent pas être recouverts par le second gâteau. Sur le dessin ce sont les trois points verts.
Or ceci est impossible car cela voudrait dire que les neuf points colorés de la figures ne sont pas recouvrables par les deux gâteaux. Ce qui contredit l'hypothèse du pâtissier.
-----------
Donc toutes les tâches pourront-être recouverte par les deux gâteaux.
CQFD.
Note à propos de la démonstration précédentes : Je n'ai montré ici que le cas où l'on a besoins de 9 points. Une démonstration rigoureuses, demanderait à étudier plusieurs autres cas. Tous ces cas ne sont pas très difficiles, mais ce serait un peu plus long. Je les laisse à l'intention du lecteur ou de la lectrice 
Il y a sûrement plus simple.
#58 - 18-06-2014 18:05:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâtezu 78
@Cogito : c'est très proche de la démo que j'avais en tête , il y a quand même pas mal de blancs laissés au lecteur ( dans ces exercices le diable se cache dans les détails ) ...
Bel effort en tout cas 
Je livre ma version dans la soirée .
Vasimolo
#59 - 18-06-2014 22:12:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteeau 78
Soit ABC le plus petit triangle recouvrant l'ensemble des taches et dont les côtés sont parallèles à ceux du gâteau modèle . Si ABC est plus petit ou égal à un gâteau , l'affaire est dans le sac , on supposera le contraire pour la suite . Chaque côté de ABC passe par une tache TA sur [BC] , TB sur [AC] et TC sur [AB] ( deux d'entre-elles peuvent être confondues ) . On note GA , GB et GC les copies du gâteau dans les angles du triangle ABC et pour finir on note EA , EB et EC les taches extérieures aux gâteaux GA , GB et GC .
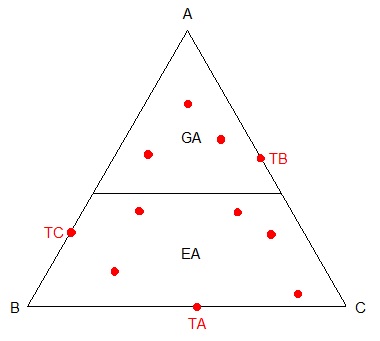
Considérons maintenant le plus petit triangle à côtés parallèles au modèle et contenant l'ensemble des points de EA ( extérieurs au gâteau GA ) . Chaque côté de ce triangle passe par une tache , l'une d'entre elle est TA . On peut faire la même chose à partir de chaque point , on a donc trois triangles dont les côtés sont parallèles au modèle et passent par neuf taches au maximum . Considérons deux gâteaux recouvrant toutes ces taches , l'un d'entre eux contient une paire de {TA,TB,TC} disons TB et TC . Or un gâteau contenant les points TB et TC ne peut contenir aucun point de EA ce qui entraine que l'autre gâteau X recouvre EA . Alors GA et X et recouvrent l'ensemble des taches .
Et c'est fini 
On peut aussi regarder ce qui se passe si le gâteau est un carré , un polygone régulier , un convexe quelconque .
Vasimolo
#60 - 19-06-2014 07:45:24
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
gâreau 78
Salut Vasimolo,
Je n'arrive pas à te suivre. Est-ce que mon image correspond au :
plus petit triangle à côtés parallèles au modèle et contenant l'ensemble des points de EA ( extérieurs au gâteau GA )
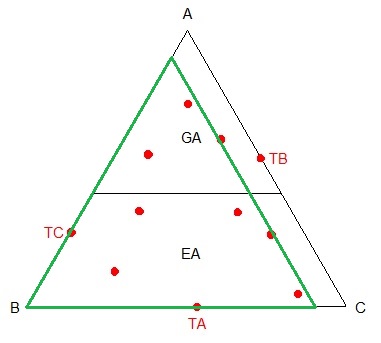
Si oui, pourquoi est-ce un ... ?
triangle dont les côtés sont parallèles au modèle et passent par neuf taches au maximum
Si je rajoute un point dans EA, alors mon triangle passera par plus de 9 points non ?
#61 - 19-06-2014 11:40:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtau 78
Salut Golgot
Ton triangle en vert est bien le plus petit triangle recouvrant EA et il a ( au moins ) une tache sur chacun de ses côtés . On considère ensuite une tache sur chaque côté ( qui peut être la même pour deux côtés ) , ce qui nous donne au maximum trois points . Si on complète avec les points des triangles recouvrant EB et EC on arrive aux neuf points annoncés .
J'espère que c'est plus clair car ce n'est vraiment pas facile à expliquer 
Vasimolo
#62 - 19-06-2014 12:03:29
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,066E+3
Gâteaau 78
Je ne comprends toujours pas... TA TB et TC sont des taches communes à tes trois triangles, donc on en revient à 6 tâches, non ?
#63 - 19-06-2014 12:08:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtea 78
C'est difficile de répondre à des bribes de question 
Si on peut recouvrir six taches avec deux triangles on peut en recouvrir neuf : qui peut le plus peut le moins .
Vasimolo
Edit : Sur le dessin de Golgot on voit bien que TB n'appartient pas au triangle recouvrant EA .
#64 - 20-06-2014 17:03:33
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
GGâteau 78
Aïe aïe aïe ma tête 
Si je comprends en partie ton raisonnement, tu utilises"uniquement" les tâches de EA, EB et EC : les 9 tâches dont tu parles et que tu choisis sont :
3 pour TA avec la tâche la plus à droite et la tâche la plus à gauche de EA (la plus à gauche relativement à la direction du côté gauche du triangle)
3 pour TB avec la tâche la plus à gauche et la tâche la plus en bas de EB.
3 pour TC avec la tâche la plus à droite et la tâche la plus en bas de EC.
On sait par hypothèse que 2 gâteaux suffisent à recouvrir n'importe quelles 9 tâches. Tu choisis ces 9 tâches précisées plus haut, alors forcément ces 2 gâteaux doivent permettre de les recouvrir. Du coup, un des 2 devra couvrir nécessairement au moins une paire de {TA,TB,TC}. Je garde ton exemple de TB et TC.
Jusque là ça va. Mais ensuite, pourquoi un gâteau couvrant TB et TC couvre nécessairement GA ?
#65 - 20-06-2014 17:39:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteauu 78
Tu as plutôt bien résumé la démarche , je suis sans doute allé un peu vite à la fin 
Un gâteau contenant TB et TC contient nécessairement le point A , il est donc "plus haut " que le triangle GA et ne rencontre pas EA .
Vasimolo
#66 - 02-07-2014 19:25:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteua 78
Je n'ai pas vraiment regardé , mais quelqu'un a-t-il essayé de voir ce que devenaient les deux versions du problème si on remplaçait les triangles équilatéraux par des carrés ?
Vasimolo
#67 - 07-07-2014 10:10:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 778
Je ne sais pas trop si quelqu’un a essayé avec les deux carrés , je donne mes premiers essais .
Rappel des problèmes :
Pb1 : Existe-t-il un entier n tel que : si on peut recouvrir n taches quelconques du plan avec deux translatés d’un carré alors on peut recouvrir l’ensemble des taches avec deux translatés du même carré ?
Pb2 : Même question en interdisant les chevauchements des carrés .
Dans les deux problèmes , si n existe , il est strictement supérieur à deux , pour s’en convaincre il suffit de prendre trois points très éloignés les uns des autres .
A propos du problème 1 : Une conjecture qui est presque une démonstration : n=3 .
A propos du problème 2 : Un exemple de cinq points ne pouvant être recouverts alors que quatre points quelconques le peuvent ( carrés de côté 2 ) . On devrait pouvoir généraliser .

A suivre ...
N'hésitez pas à donner vos idées .
Vasimolo
#68 - 11-07-2014 11:45:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâtrau 78
Allons-y pour la suite avec les carrés et recouvrements autorisés 
Propriété : Si on peut recouvrir trois taches quelconques avec deux carrés ( translatés du modèle ) alors on peut recouvrir l'ensemble des taches avec deux carrés .
Preuve : On enferme toutes les taches dans le plus petit rectangle ( éventuellement aplati ) dont les côtés sont parallèles à ceux du modèle . Si on note x la longueur et y la largeur de ce rectangle , il y a quatre cas de figure :
y≤1
1<y≤x≤2
1<y≤2<x
2<y≤x
illustrés ci-dessous :

Il y a nécessairement au moins une tache sur chaque bord , la même tache pouvant servir deux fois si elle est au sommet du rectangle . Sur chaque dessin la zone rouge ne peut pas contenir de tache et les zones bleues sont « clivantes » dans le sens ou aucun des deux carrés utilisés ne peut pas empiéter sur deux composantes connexes bleues . Dans tous les cas il ne peut pas y avoir une tache dans trois composantes bleues . Alors toutes les taches sont dans deux zones bleues et éventuellement dans les zones jaunes , on peut les recouvrir avec deux carrés .
@suivre …
Vasimolo
#69 - 13-07-2014 12:51:30
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtaeu 78
Pour le deuxième problème :
J'ai un exemple de 6 points ne pouvant pas être recouverts par deux carrés de côté 3 ( mais 5 quelconques d'entre eux : oui ) .

Et sept points non recouvrables par deux carrés de côté 4 :

Pour le moment je n'ai pas de configuration type que l'on pourrait étendre à tout entier comme celle du message #55 de Cogito pour les triangles équilatéraux .
@suivre ...
Vasimolo
#70 - 15-07-2014 12:48:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteua 78
Huit points et deux carrés de côté 5, mais là c'est trop facile avec toutes ces symétries 

Vasimolo
#71 - 18-08-2014 11:41:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâreau 78
Histoire de réanimer un peu le problème : quelqu'un a-t-il réussi à trouver un ensemble de 9 points qui ne peuvent pas être recouverts par deux carrés alors que 8 d'entre eux le peuvent toujours ?
Vasimolo
#72 - 18-08-2014 15:18:50
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,066E+3
Gâtea u78
Ce n'est plus de la réanimation, c'est de l'acharnement thérapeutique 
#73 - 18-08-2014 18:30:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
âteau 78
Il n'est pas moribond ce problème , j'aimerais bien une solution complète pour le carré comme cela a été fait pour le triangle équilatéral .
Courir après chaque problème qui montre une fesse c'est pas mal , j'aime bien m'attarder sur ceux qui montrent un peu plus 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum

















