|
#1 - 07-11-2014 09:42:09
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Le troupeau en amrche
salut à tous.
je propose une petite énigme en espérant qu'elle va intéresser quelques uns .
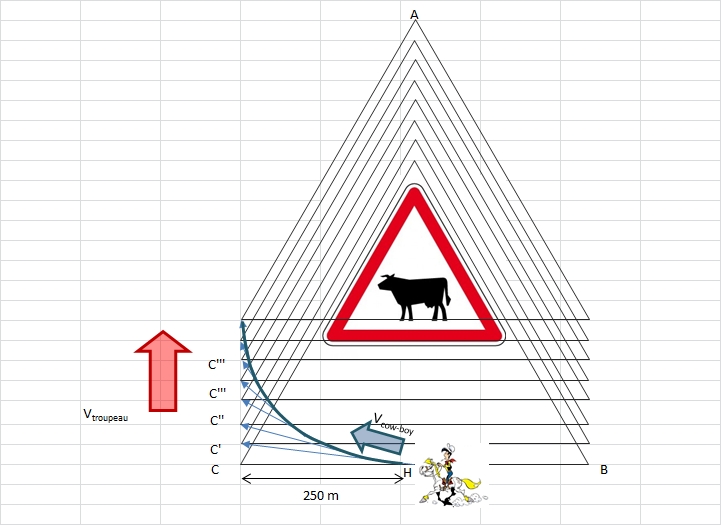
Un troupeau de bétail en forme de triangle équilatéral ABC de 500m de côté avance à vitesse constante dans la direction HA , H étant le milieu de BC .
La tête du troupeau se trouve donc en A .
Durant la traversée de la grande plaine , un des cowboys est positionné en H .
A midi , il décide de faire le tour du troupeau afin de s'assurer que tout roule à merveille. Il démarre donc au trot --- son cheval trottant lui aussi à vitesse constante --- pour revenir en H à midi et douze minutes exactement. Durant son inspection , le troupeau aura alors parcouru 500m , et l'inspection du cowboy , elle , aura duré 12 min.
A quelle heure est-il passé en A ? . La réponse sera arrondie au dixième de seconde.
bon courage.
#2 - 07-11-2014 19:08:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Le troupeau en marce
Bonjour
Un problème intéressant qui rappelle un peu celui d'une barque qui perd un objet sur une rivière à flot continu .
J'y réfléchis dès que je trouve un moment 
Vasimolo
#3 - 07-11-2014 22:47:13
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le torupeau en marche
Proposition:
Je donne une réponse, si c'est la bonne, je développerai mon raisonnement.
Il passe en A à midi 7 minutes et 5.8 secondes soit 425.8 secondes après son départ.
J'ai aussi le reste des paramètres (visite, distance totale parcourue, passage aux différents sommets)!
#4 - 07-11-2014 23:45:44
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Le troupau en marche
salut.
kossi_tg: réponse bonne . tu peux développer stp.
#5 - 08-11-2014 00:10:36
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
eL troupeau en marche
Moi, si vasimolo s'est planté sur un truc de maths, je réfléchis même pas. 
#6 - 08-11-2014 11:54:06
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
le troupezu en marche
[TeX]V_t[/latex]: vitesse du troupeau = 500/(12*60)=0.6944m/s
[latex]V_c[/latex]: vitesse constante du cow boy
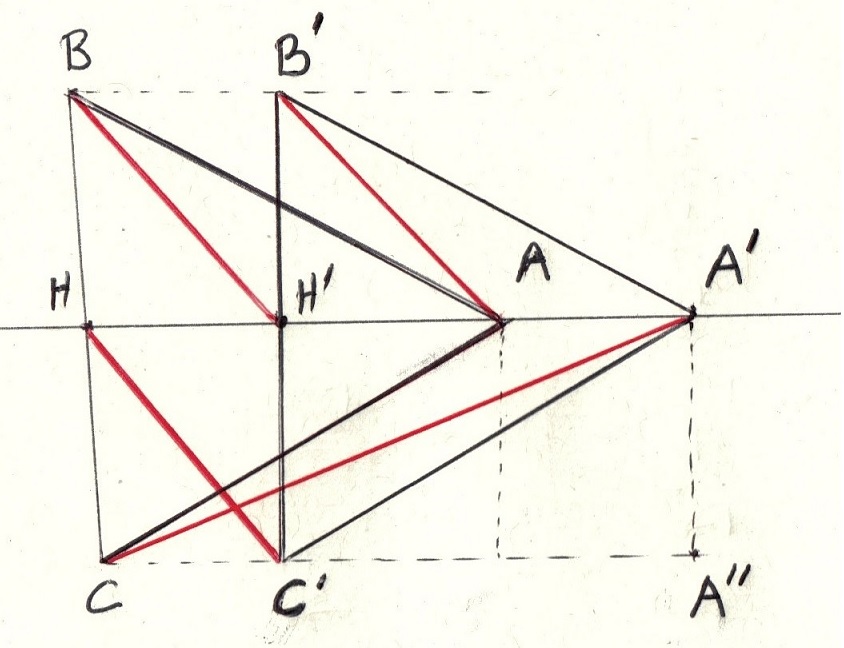
J'ai découpé le parcours en 4 étapes représentées par HC', CA', AB' et BH' (liaison entre 2 sommets). Pour chaque étape, je considère ABC comme la position initiale du troupeau et A'B'C' la position du troupeau quand l'étape est terminée. La première et dernière (HC' et BH') sont identiques.
Première étape: HC'
Soit t_1, le temps de cette étape, on a: V2c=V2t+(HC/t1)[/TeX][TeX]Vt et (HC/t1) étant des composantes de Vc dans cette étape.
On déduit: t1=HC√V2c−V2t;
Deuxième étape: CA'
Soit t2, le temps de cette étape
CA′2=CH2+HA′2 (pythagore)
HA'=\sqrt{3}*HC+V_t*t_2[/TeX] [TeX]CA'=t_2*V_c[/TeX] On déduit de ces 3 équations: [TeX]t_2=\frac{\sqrt{3}*CH*V_t}{D}+ \sqrt{\frac{4*HC^2}{D}+\frac{3*HC^2*V-t^2}{D^2}} où [latex]D=\sqrt{V_c^2-V_t^2}[/TeX]
Troisième étape: AB'
Soit t_3, le temps de cette étape
Le même raisonnement que l'étape précédente; on arrive à:
t_3=-\frac{\sqrt{3}*CH*V_t}{D}+ \sqrt{\frac{4*HC^2}{D}+\frac{3*HC^2*V-t^2}{D^2}}
Quatrième étape: BH'
Cette étape est identique à la première t_4=t_1.
La durée totale du parcours est de T=t_1+t_2+t_3+t_4=12*60=720 s
Tout calcul bien fait à partir de cette relation donne:
2*HC*(\sqrt{D}+\sqrt{4*D+3*V_t^2})=T*D[/latex] soit [latex](\sqrt{D}+\sqrt{4*D+3*V_t^2})=1.44*D[/latex] car T=720 et CH=250. Méthode du point fixe: [latex]D=4.5679324579297=V_c-V_t[/latex] où [latex]V_t=0.69444
V_c=2.24726178812115
On a alors:
t_1=t_4=116.971530332742
t_2=308.857653433083
t_3=177.199285901433
Il passe par la tête du troupeau après les 2 premières étapes soit t_1+t_2=425.829183765825=~7min et 5.8 sec
donc midi 7 min et 5.8 secondes.
A l'arrivée à son point de départ, il aura parcouru 1628.03 m.
(Les formules Latex semblent rencontrer des problèmes d'affichages!) Je mettrai le scan de mes brouillons si cela ne s'améliore pas.
#7 - 08-11-2014 16:34:11
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Le toupeau en marche
J’ai trouvé 12 h 07 mn 05,8 s.
Pour arriver à ce résultat j’ai utilisé une méthode assez bourrin. Je ne doute pas qu’on cherche une méthode bien plus élégante, mais je ne l’ai pas trouvée.
J’appelle v1, v2 et v3 les vitesses du cow-boy dans le référentiel mobile attaché au troupeau sur les tronçons respectifs CB, BA et AC, vm la vitesse constante du cow-boy dans le référentiel fixe (attaché à la plaine), vt la vitesse du troupeau (qui est de 2,5 km/h), T le temps mis par le cow-boy pour faire un tour (12 mn = 1/5 h) et L le côté du triangle équilatéral (500 m = 1/2 km).
J’étudie les vecteurs vitesse sur chacun des tronçons en posant: k = vm/vt.
v1 = vt.(k²-1)^(1/2)
v2 = vt.[(4.k²-1)^(1/2)-3^(1/2)]/2
v3 = vt.[(4.k²-1)^(1/2)+3^(1/2)]/2
Or j’ai aussi: T = L/v1 + L/v2 + L/v3; d’où:
1/[(k²-1)^(1/2)] + 2/[(4.k²-1)^(1/2) - 3^(1/2)]/2 + 2/[(4.k²-1)^(1/2) + 3^(1/2)]/2
= T.vt/L = 1
Je simplifie tout ça en posant: m = (k²-1)^(1/2), soit: k = (m²+1)^(1/2) et je trouve:
m^4 - 2.m^3 - 3.m^2 - 3 = 0, équation du quatrième degré.
Une dichotomie me donne des valeurs approchées: m = 3,07766; soit: k = 3,23605.
Au final j’ai: v1 = 3,07766.vt; v2 = 2,33116.vt et v3 = 4,06321.vt.
Puis je calcule mes heures de passage aux différents points:
- départ de H à 12 h 00 mn 00,0 sec,
- passage en B à 12 h 01 mn 57,0 sec,
- passage en A à 12 h 07 mn 05,8 sec,
- passage en C à 12 h 10 mn 03,0 sec,
- arrivée en H à 12 h 12 mn 00,0 sec.
Merci pour cette énigme.
#8 - 08-11-2014 18:33:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
eL troupeau en marche
Bon , on arrive à mettre le problème en équation mais je n'en tire pas grand chose de propre sans logiciel de calcul .
Y-a-t-il une solution simple à ce problème ?
Vasimolo
#9 - 08-11-2014 18:47:27
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Le trupeau en marche
salut à tous.
kossi & franky le résultat est correct . mais j'ai du mal à suivre sans l'écriture avec latex.
vasimolo: il y a une résolution d'équation (de degré 4) qui se résout bien avec calculette genre Ti85
je possède ce vieux modèle . je donnerai plus tard ma résolution , en espérant que latex refonctionne .
#10 - 09-11-2014 18:47:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Le troupeau en arche
Sauf erreur , j'ai trouvé 12h 07m 05,8 s .
Je ne suis pas sûr du tout du résultat et absolument pas satisfait de la méthode à coup de valeurs approchées 
Vasimolo
#11 - 09-11-2014 18:58:31
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Le toupeau en marche
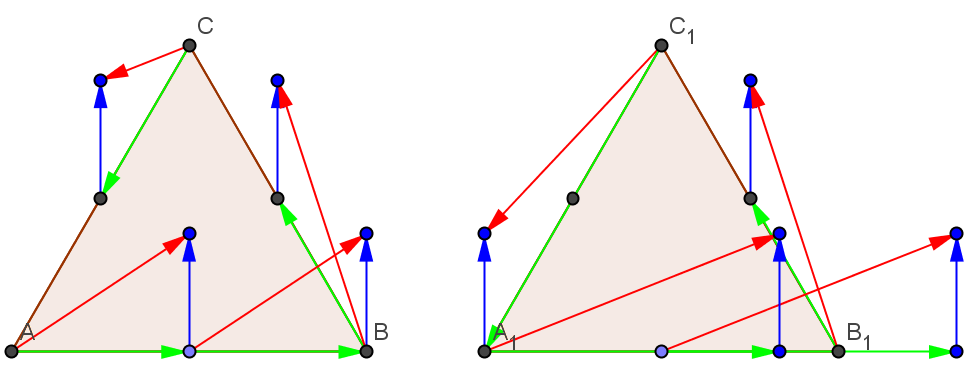
En bleu : le vecteur vitesse du troupeau par rapport au sol.
En vert : les vecteurs vitesses du cowboy par rapport au troupeau sur les différentes sections du trajet.
En rouge : les vecteurs vitesses du cowboy par rapport au sol sur les différentes sections du trajet.
Dans l'image de gauche on se place dans une situation ou la vitesse du cowboy par rapport au troupeau est constante. Il apparait alors que la section de trajet BC est la section ou le cowboy se déplace le plus rapidement par rapport au sol.
Pour que le cowboy puisse faire le tour du troupeau à vitesse par rapport au sol constante il faut donc que cette vitesse soit celle que l'on observe sur la section de trajet BC dans l'image de gauche, ce qui nous amène à quelque chose ressemblant à l'image de droite.
Après quelques calculs on obtient alors :
V(Cowboy/Troupeau) = 95.25 m/min
D’où :
T(A) = 7.13 min = 427.8 s

#12 - 09-11-2014 19:46:15
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
le troupeau en matche
salut.
vasimolo : oui pour le résultat.
sydre : non
#13 - 09-11-2014 19:54:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#14 - 09-11-2014 20:38:15
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
le troupzau en marche
salut.
vasimolo.
le polynôme de degré 4 n'est pas monstrueux . tous ses coefficients sont entiers.
#15 - 10-11-2014 11:06:18
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
le troupeau en mzrche
salut à tous.
et merci à tous ceux qui ont cogité dur sur le problème. la réponse attendue était celle-ci : 12h 7min 5s et 8/10s
j'ai résolu le problème , il est écrit sous latex , pour le moment il m'est impossible de vérifier la syntaxe et je le posterai dès que le problème laTex sur le forum sera résolu .
merci de votre compréhension.
#16 - 10-11-2014 22:37:39
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
Le truopeau en marche
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#17 - 10-11-2014 22:44:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Le tropeau en marche
J'en pense que non, car le cowboy avance en ligne droite. Ce sont deux vecteurs constants qui déterminent sa trajectoire sur chaque partie du parcours, la première et la quatrieme étant identiques. Là, Lucky luke a l'air d'avoir bu.
#18 - 10-11-2014 22:47:31
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
le troupeau en larche
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#19 - 10-11-2014 22:52:00
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
le troupeau en marvhe
Je suis d'accord avec Gwen, même si je n'ai pas eu le temps de m'intéresser au problème.
Si le troupeau avance, le cowboy n'a aucun intérêt à avancer avec une tangente "horizontal" au départ...
Cette courbe que tu proposes correspondrait à une avance uniformément accélérée du troupeau.
La meilleure preuve, c'est d'imaginer que le triangle a ses côtés 2 fois plus long, en supposant que lucky luke démarre comme tu l'as fait, comment se terminerait la 2ème partie du premier segment ?
PS : Vous voyez quelque chose au message de Kossi_tg ?
#20 - 14-11-2014 14:54:36
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Le troupeau n marche
Salut à tous.
Je poste quand même ma résolution en souhaitant que laTex refonctionne un jour.
Je n'ai aucune Prévisualisation pour le moment , je corrigerai s'il le faut par la suite.
Je ne comprend pas car laTex fonctionne sur certains postes en amont.
solution:
dans ce problème , les vitesses Vt (troupeau) et Vc (cowboy) sont constantes . Alors on peut écrire :
\frac{V_c}{V_t}=\frac{D_c}{D_t} = x [/latex], D étant les distances parcourues c'est cette variable x qu'on va devoir trouver . On peut aussi remarquer que le cowboy a la possibilité de démarrer son inspection à partir d'un point quelconque sur un des côtés du triangle. alors pour résoudre la problème , je vais le placer en B . Il va ainsi longer dans cet ordre les 3 côtés BC , CA & AB . Durant ces 3 phases de déplacement du cowboy , le troupeau aura parcouru 3 distances : a , b & c Et a+b+c=500 phase 1 : le cowboy parcourt le segment BC en mouvement pendant que le troupeau , lui , parcourt la distance a . a+b+c=500 [latex] a^2 = a^2x^2 - 500^2 \Rightarrow a = \frac{500}{\sqrt{x^2-1}} [/latex] (1) phase 2 : le cowboy parcourt le segment CA en mouvement pendant que le troupeau , lui , parcourt la distance b . [latex]250^2 + (250\sqrt3 + b)^2 = b^2x^2 [/latex]d'où l'équation : [latex] (x^2-1).b^2 - 500\sqrt3.b - 500^2 = 0 [/latex] équation du second degré en b Ce qui donne : [latex] b = \frac{500\sqrt3 + \sqrt{750000 + 10^6.(x^2-1)}}{2.(x^2-1)} [/latex] (2) phase 3 : le cowboy parcourt le segment AB en mouvement pendant que le troupeau , lui , parcourt la distance c . [latex] 250^2 + (250\sqrt3 - c) ^2= c^2.x^2 [/latex]d'où l'équation du second degré en c [latex] (x^2-1).c^2 + 500\sqrt3.c - 500^2 = 0
ce qui donne :
c = \frac{-500\sqrt3 + \sqrt{750000 + 10^6.(x^2-1)}}{2.(x^2-1)} [/latex] (3) Ainsi en sommant a , b et c , on obtient l'égalité suivante: [latex] a+b+c = \frac{500}{\sqrt{x^2-1}} + \frac{500.\sqrt{3+4x^2-4}}{x^2-1} = 500 \frac{\sqrt{4x^2-1}}{x^2-1} = \frac{\sqrt{x^2-1} - 1}{\sqrt{x^2-1}} \frac{4x^2-1}{(x^2-1)^2} = \frac{x^2 - 2.\sqrt{x^2-1}}{x^2-1}\Rightarrow\frac{4x^2-1}{x^2-1} = x^2 - 2.\sqrt{x^2-1}
\frac{4x^2-1}{x^2-1} - x^2 = -2.\sqrt{x^2-1} \frac{x^4-5x^2+1}{x^2-1} = 2.\sqrt{x^2-1} x^4-5x^2+1 = 2.(x^2-1).\sqrt{x^2-1}
puis en posant x^2 = X et en élevant tout au carré pour faire disparaître le radical , on obtient une équation de degré 4 en X :
X^4 -14X^3 + 39X^2 -22X +5 = 0 [/latex]qui donne : [latex]X\approx10.472065 \Rightarrow x=\sqrt{X}\approx 3.236057
Le cowboy aura ainsi parcouru : 500x \approx1618.028 m
puis en reportant la valeur de x dans les expressions (1) , (2) & (3) on obtient les valeurs a , b & c correspondant aux distances parcourues par le troupeau durant chacune de ces 3 phases . Mais comme aussi le cowboy démarre en H au lieu de B , le troupeau aura parcouru : a/2 + b lorsque le
cowboy sera en A . et:
a = 162.46046 m\Rightarrow\frac{a}{2} = 81.23023 m
b = 214.48448 m
c = 123.05506 m
et \frac{a}{2}+ b = 295.715 m
le troupeau ayant parcouru 500 mètres en 12 min , le cowboy sera passé en A à : 12h + 720.\frac{295.715}{500}s = 12h+7min+5s+83/100s
Patience et longueur de temps .......
|
 |

 Accueil
Accueil
 Forum
Forum