Enigme Marche aléatoire sur un icosaèdre @ Prise2Tete

Ebichu · #1

Bonjour à tous.

Une fourmi, qui n'a rien de mieux à faire, se déplace le long des arêtes d'un icosaèdre régulier. Elle part d'un sommet, et son objectif est d'atteindre le sommet opposé de l'icosaèdre.

Combien d'arêtes peut-elle espérer parcourir avant d'atteindre son but, si après avoir atteint un nouveau sommet :

(1) elle se déplace avec la même probabilité vers un des sommets voisins, y compris celui dont elle vient.

(2) elle se déplace avec la même probabilité vers un des sommets voisins, celui dont elle vient n'étant pas compris (c'est-à-dire qu'elle ne passe pas deux fois de suite sur une même arête).

Amusez-vous bien !

caduk · #2

Bonjour,
sauf erreur de calcul, je trouve:
1) 18
2) 15

Ebichu · #3

Je ne trouve pas comme toi

Peux-tu détailler ton raisonnement ?

caduk · #4

On a clairement une chaîne de Markov.
Transcrivons notre icosaèdre sous forme de graphe:

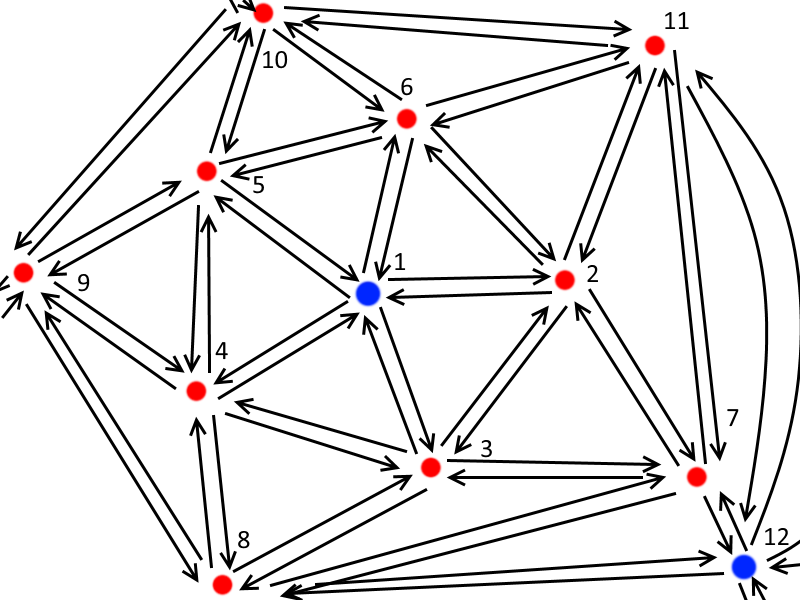
Il y a aussi pour chaque sommet une transition du sommet à lui-même.
Chacune des transitions se fait avec une probabilité de 1/6.
On cherche à aller du sommet 1 au sommet 12
Notons E1, E2, ..., E12 , ou En est le temps moyen pour atteindre le sommet 12 à partir du sommet n (En = E(T|X0 = n) avec Xn = sommet atteint à l'étape n et T=inf{n∈N;Xn∈A} )

En appliquant la méthode à un pas, on obtient le système suivant:
E1 = 1 + (1/6)E1 + (1/6)E2 + ... + (1/6)E6
E11 = 1 + (1/6)E11 + (1/6)E2 + (1/6)E6 + ... + (1/6)E10 + (1/6)E12
E12 = 0 (car en partant du sommet 12, on est déjà arrivé au sommet 12

En écrivant sous forme standard d'un système linéaire et en se débarassant de E12, on obtient:
5E1 - E2 - E3 - ... - E6 = 6
...
5E11 - E2 - E6 - ... - E10 - 0 = 6
Ce qui s'écrit sous forme matricielle:
Ax = b avec:
xt = (E1, E2, ...., E11)
A =
5 -1 -1 -1 -1 -1 0 0 0 0 0
-1 5 -1 0 0 -1 -1 0 0 0 -1
-1 -1 5 -1 0 0 -1 -1 0 0 0
-1 0 -1 5 -1 0 0 -1 -1 0 0
-1 0 0 -1 5 -1 0 0 -1 -1 0
-1 -1 0 0 -1 5 0 0 0 -1 -1
0 -1 -1 0 0 0 5 -1 0 0 -1
0 0 -1 -1 0 0 -1 5 -1 0 0
0 0 0 -1 -1 0 0 -1 5 -1 0
0 0 0 0 -1 -1 0 0 -1 5 -1
0 -1 0 0 0 -1 -1 0 0 -1 5
bt = (6,6,6,6,6,6,6,6,6,6,6)

donc x = A^(-1)b =
18.0000
16.8000
16.8000
16.8000
16.8000
16.8000
13.2000
13.2000
13.2000
13.2000
13.2000

Donc E1 = 18

Pour la deuxième partie, on n'écrit de la même manière le système. Après l'avoir simplifié, on se rend que dans le système matriciel, la matrice A est exactement la même, et que b = (5,5,5,5,5,5,5,5,5,5,5)
Après résolution, on trouve alors x =
15.0000
14.0000
14.0000
14.0000
14.0000
14.0000
11.0000
11.0000
11.0000
11.0000
11.0000

Donc E1 = 15

Edit:
Je suis un peu stupide, on peut aller beaucoup plus rapidement...
En utilisant les symétries, on note x1 l'espérance en partant du sommet 1, x2 l'espérance en partant du sommet 2,3,4,5 ou 6 , x3 en partant du sommet 7,8,9,10 ou 11, et x4 en partant du sommet 12.
De la même manière, en appliquant la méthode à 1 pas, on obtient le sytème:
x1 = 1 + (x1 + 5x2)/6
x2 = 1 + (3x2 + x1 + 2x3)/6
x3 = 1 + (3x3 + 2x2 + x4)/6
x4 = 0
En l'écrivant sous forme matricielle, on a
A =
5 -5 0
-1 3 -2
0 -2 3
b =
6
6
6
et on obtient bien x =
18.0000
16.8000
13.2000
en résolvant le système d'ordre 3, ce qui est beaucoup plus simple à résoudre à la main...
de même, on retrouve le résultat de la 2

Ebichu · #5

@caduk : ta méthode est bonne, mais tu n'as pas interprété l'énoncé comme je l'escomptais.

En supposant que les sommets sont numérotés, dans la question (1), on peut avoir le trajet 1-2-1, mais pas dans la question (2), car on passerait alors deux fois de suite sur l'arête 1-2. Par contre, on ne peut jamais avoir le trajet 1-1 car il n'y a pas d'arête reliant un sommet à lui-même.

Par conséquent, la réponse que tu donnes à la question (2) est celle attendue pour la question (1), et tu as déjà résolu la moitié du problème

gwen27 · #6

Désolé, mais encore une fois, je ne comprends pas la question... Elle peut aussi bien espérer parcourir 3 arêtes que 50 ou plus...

Tu attends quoi ? Une moyenne ?

nodgim · #7

Salut Ebichu,
J'avance 15 pour le 1er scénario et seulement 5,69 ( ! ) pour le second.
Si c'est bon, je donnerais une explication de ma méthode.

Ebichu · #8

@gwen27 : "espérer" fait référence à l'espérance, cf vocabulaire des probabilités. C'est comme la moyenne, mais ce terme est plus approprié ici.

@nodgim : je trouve comme toi pour le 1er scénario mais pas pour le 2e.

nodgim · #9

J'ai vu une erreur de retranscription sur tableur, je trouve maintenant 11,4 pour le scénario 2.
Il faudrait que je revérifie tout ça.

Ebichu · #10

@nodgim : maintenant, je trouve comme toi. Bravo ! Tu expliques ta méthode ?

nodgim · #11

Pour le scénario 1, je modélise l'isocaèdre comme une tour à 3 étages :
- B le bas, qui est le départ, qui est le sommet inférieur de l'isocaèdre.
-1, le 1er étage, qui est le niveau des 5 sommets atteints après un déplacement depuis le bas vers le haut.
-2, le 2ème étage des 5 sommets suivants.
-H, le sommet du haut.

A partir de là je représente un graphe d'échanges entre ces 4 objets, avec les distributions des probas ( toutes les flêches qui partent d'un objet ont un total de 1 )
Sans faire la liste, on peut en décrire un exemple :
1-----( 0,4 )------> 1
1-----( 0,4 )------> 2
1-----( 0,2 )------> B

A partir de là, on déduit l'expression de chaque objet d'indice (nb de déplacements) n+1 par les flêches entrantes issus des objets indice n.
Exemple : B ( n + 1) = 0, 2 * 1 (n)

Ensuite on met sur tableur et on crée une colonne supplémentaire pour le calcul de l'espérance.

Pour le scénario 2, c'est un plus compliqué, puisque la destination à partir d' un objet dépend du déplacement précédent. Il faut distinguer ces objets selon la provenance du dernier déplacement.
Les objets sont :
B, 1 après B (1pB), 1p1, 1p2, 2p1, 2p2, H.

On fait alors comme pour le scénario 1.

Ebichu · #12

@nodgim : OK, nous avons fait la même modélisation. C'est probablement la méthode la plus efficace. Par contre, je ne comprends pas ce que tu fais avec le tableur, peut-être peux-tu me faire une copie d'écran ?

enigmatus · #13

Bonsoir,
Sauf erreur, le nombre moyen d'arêtes est de 15 dans le premier cas, et de 11,4 dans le second.

Ebichu · #14

@enigmatus : bravo, bonne réponse ! Une explication ?

enigmatus · #15

@Ebichu #14

Problème n° 1 :

Sur l'icosaèdre, on peut distinguer 4 types de sommets :
_ 1 sommet de type 0 (celui de départ)
_ 5 sommets de type 1 (ceux contigus à celui de type 0)
_ 5 sommets de type 2 (ceux contigus à celui de type 3)
_ 1 sommet de type 3 (celui d'arrivée)

Si on appelle Pn la longueur moyenne du parcours à partir d'un sommet de type n, on a les relations :

Code:

P0 = 1 + P1
P1 = 1 + (P0 + 2*P1 + 2*P2) / 5
P2 = 1 + (2*P1 + 2*P2 + P3) / 5
P3 = 0

D'où P0 = 15

Problème n° 2 :

C'est un peu plus compliqué. On appelle Pmn la longueur moyenne du parcours à partir d'un sommet de type n, sachant que l'on vient d'un sommet de type m.
On a les relations :

Code:

P10 = 1 + P01
P01 = 1 + (P11 + P12) / 2
P11 = 1 + (P10 + P11 + 2*P12) / 4
P12 = 1 + (P21 + 2*P22 + P23) / 4
P21 = 1 + (P10 + 2*P11 + P12) / 4
P22 = 1 + (2*P21 + P22 + P23) / 4
P23 = 0

D'où P10 = 11,4

nodgim · #16

..............B.............Et 1..............Et 2...............H
0............1...............0..................0.................0
1............0...............1..................0.................0
2...........0,2...........0,4................0,4................0
3..........0,08..........0,52..............0,32............0,08.............0,24
4..........0,104.......0,416.............0,336..........0,064............0,496
5.........0,0832.....0,4048............0,3008........0,0672...........0,832
6........0,08096....0,36544..........0,28224.......0,06016.........1,19296
7.......0,073088..0,340032.........0,259072.... 0,056448.........1,588096

Voila un extrait du résultat pour le scénario 1.

Les formules :
B(n+1)= 0,2 Et1 (n)
Et1 (n+1)= 0,4 * (Et1 (n) + Et2(n) ) + B(n)
Et2 ( n+1 ) = 0,4 * ( Et1(n) + Et2(n) )
H ( n+1) = 0,2 * Et2
La dernière colonne est l'espérance. Le résultat apparait au bout d'un peu plus de 300 lignes.

Il y a peut être une manière de faire un calcul direct pour trouver 15, mais je ne maîtrise pas trop la technique de ce calcul.

Ebichu · #17

@enigmatus : parfait, nous avons procédé de la même façon.

@nodgim : cette méthode empirique est intéressante, même si elle n'est pas pleinement satisfaisante, vu que c'est une observation plus qu'une preuve. Il existe effectivement un calcul direct, et même si tu ne connais pas la méthode, tu peux l'imaginer sans trop de difficulté je pense :
Spoiler : [Afficher le message]

caduk · #18

Pour la deuxième question, on peut retrouver une chaine de markov en regroupant les états au n-ième et au n+1ième déplacements. On obtient alors le schéma suivant:

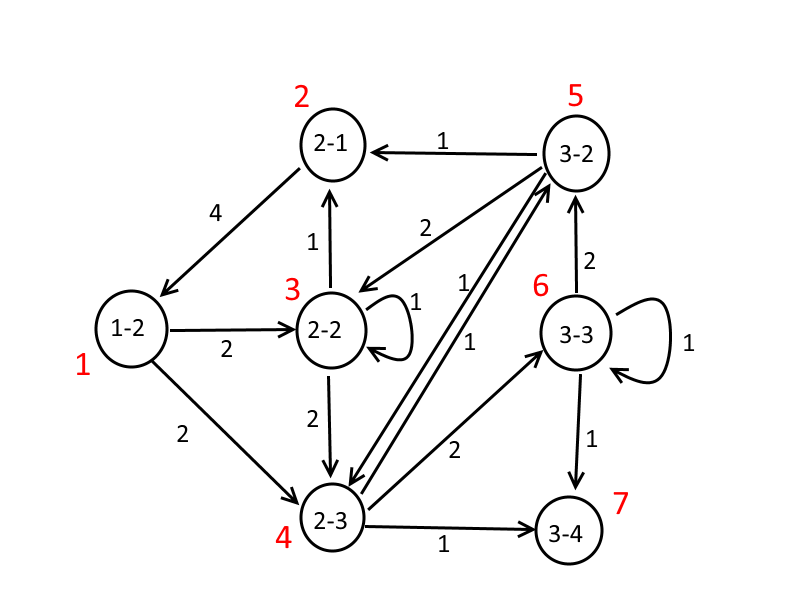
(diviser par 4 chacune des probabilités de transition). Les numéros 1,2,3,4 correspondent aux 4 classes de sommets que j'ai définies à la fin de mon premier post.
On obtient après avoir écrit le système correspondant à la méthode à 1 pas le système matriciel:
Ax = b
A =

4 0 -2 -2 0 0
-4 4 0 0 0 0
0 -1 3 -2 0 0
0 0 0 4 -1 -2
0 -1 -2 -1 4 0
0 0 0 0 -2 3

b =

4
4
4
4
4
4

qui donne
x =

10.4000
11.4000
10.6000
8.2000
11.2000
8.8000

Ainsi, l'espérance pour arriver en 4 après avoir atteint un sommet de type 2 juste après être parti de 1 est 10.4000
En partant de 1, l'espérance est donc de 10.4 + 1 = 11.4

Ebichu · #19

@caduk : parfait !

Franky1103 · #20

Les sommets de l’icosaèdre sont situés sur 4 étages: 1 en haut, 5 juste en dessous, 5 encore en dessous et 1 en bas. En appelant respectivement n1, n2 et n3 le nombre d’arêtes parcourus pour passer respectivement de l’étage du haut, de l’étage juste en dessous et de l’étage encore en dessous à celui du bas, on a les relations:
n3 = 2(n2+1)/5 + 2(n3+1)/5 + 1/5 => 3n3 = 2n2 + 5 => n2 = (3n3–5)/2
n2 = (n1+1)/5 + 2(n2+1)/5 + 2(n3+1)/5 => 3n2 = n1 + 2n3 + 5 => n1 = 5(n3–5)/2
J’ai trois inconnues mais seulement deux équations: quelque chose m’échappe encore pour une troisième équation: affaire à suivre .....

Ebichu · #21

@Franky1103 : tu as la bonne méthode, et effectivement, il te manque une équation.

Spoiler : [Afficher le message]

Franky1103 · #22

Mais bien sûr !!! On a en plus: n1 = n2+1, ce qui donne: n1 = 15 pour la première question (avec n2 = 14 et n3 = 11). Il reste à voir la seconde question .....

Ebichu · #23

C'est terminé, merci à ceux qui ont cherché et félicitations à ceux qui ont trouvé.

Il y a suffisamment de bonnes réponses pour que je puisse m'abstenir de rajouter quoi que ce soit, je crois que tout a été dit.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 14-03-2017 22:59:20

Marche aléatoire sur un icoasèdre

#0 Pub

#2 - 15-03-2017 00:11:13

Marche aléatoir sur un icosaèdre

#3 - 15-03-2017 00:18:06

marche akéatoire sur un icosaèdre

#4 - 15-03-2017 13:33:30

Marcche aléatoire sur un icosaèdre

#5 - 15-03-2017 15:24:49

marvhe aléatoire sur un icosaèdre

#6 - 15-03-2017 17:09:45

Marchhe aléatoire sur un icosaèdre

#7 - 15-03-2017 17:32:42

Marche aléatoire sur u icosaèdre

#8 - 15-03-2017 17:39:40

Marche aléatoire sur u icosaèdre

#9 - 15-03-2017 18:50:13

Marche aaléatoire sur un icosaèdre

#10 - 15-03-2017 19:02:08

Marche aléatoire sur nu icosaèdre

#11 - 15-03-2017 19:40:07

marche aléatoire sir un icosaèdre

#12 - 15-03-2017 20:38:09

marche aléatoiee sur un icosaèdre

#13 - 15-03-2017 21:00:53

marxhe aléatoire sur un icosaèdre

#14 - 15-03-2017 21:53:57

Marche aléatoire sur un icosaèèdre

#15 - 16-03-2017 07:44:05

Marche aléatoire sur un icsoaèdre

Code:

Code:

#16 - 16-03-2017 07:54:48

Marche aéatoire sur un icosaèdre

#17 - 16-03-2017 09:37:32

Marche aléatoire surr un icosaèdre

#18 - 16-03-2017 15:52:56

Marche aléatoire sur uun icosaèdre

#19 - 16-03-2017 18:38:13

Marche aélatoire sur un icosaèdre

#20 - 17-03-2017 17:11:38

marche aléatoire sur un icosaèsre

#21 - 17-03-2017 21:00:12

Marrche aléatoire sur un icosaèdre

#22 - 19-03-2017 03:21:15

marche aléatpire sur un icosaèdre

#23 - 19-03-2017 15:50:19

Marche aléatoire sur un icosadre

Réponse rapide

Sujets similaires

Pied de page des forums