|
#1 - 26-12-2014 19:07:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 26-12-2014 20:40:32
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâeau 86
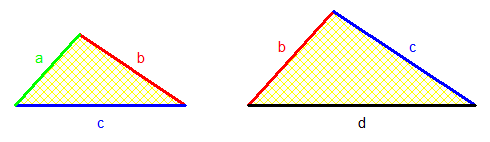
19, 38, 76 et le double : 38, 76, 152 ce qui donne 399 cm
#3 - 26-12-2014 20:41:31
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
âGteau 86
Bonsoir,
J'ai trouvé 2 solutions (valeurs en cm) :
a=19 b=38 c=76 d=152 reste=1
a=27 b=45 c=75 d=125 reste=8
Ajouté :
Si on accepte que le gâteau de gauche puisse être le plus grand, on a en plus
a=125 b=75 c=45 d=27 reste=8
a=152 b=76 c=38 d=19 reste=1
Édité : Si je tiens compte de la remarque (tout à fait justifiée) de Vasimolo en #4, il ne me reste plus aucune solution.
#4 - 26-12-2014 21:11:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtea 86
Ne pas oublier qu'il existe une inégalité dite "triangulaire" 
Vasimolo
#5 - 26-12-2014 21:24:21
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
gâtezu 86
oups oui 19+38 c'est dur d'avoir un triangle à 76 
#6 - 26-12-2014 23:15:41
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 68
Après de vains efforts de résolution "carrée" (d'un polynôme de degré 3), la meilleure solution a été une bête recherche sur excel par tatonnement, qui me donne :
a=27; b=45; c=75 et d=125, avec un rapport de 5/3 pour une longueur totale de 392 cm, et donc un reste de 8 cm.
Bien prise de tête celle-ci ! J'attends avec impatience une réponse argumentée ^^
#7 - 27-12-2014 09:31:34
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
gâreau 86
Deux solutions qui ne correspondent pas tout à fait à l'énoncé :
Deux triangles équilatéraux de 65 ou 66 cm de côté, il n'a qu'à faire celui des parents plus épais 
Sinon , on est limités par un rapport de (1+rac(5))/2 , donc pas de solution entière.
#8 - 27-12-2014 10:05:06
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gââteau 86
salut.
j'ai une solution avec un reste de ruban de 20 cm (moins de 10 je ne vois pas)
les 2 triangles sont semblables et tous leurs côtés sont entiers .
appelons n le plus petit côté . alors :
n.(1 + 2q + 2q^2 + q^3) = 390+u avec q rationnel et 1<q<(1+V5)/2 et enfin 0<u<10
q = a/b alors n est divisible par b^3
avec n=32 et q=3/2 , j'ai les triangles 32 , 48 , 72 et 48 , 72 & 108 dont la somme des côtés vaut 380.
je continue à chercher.
#9 - 27-12-2014 10:18:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtteau 86
Si on laisse de côté la longueur du reste de ruban , il n'y a que cinq paires de gâteaux qui satisfont aux exigences du pâtissier . Il n'y a plus qu'à calculer le reste pour chacune d'entre elles .
C'est bien plus simple et plus rapide que ça en a l'air 
Vasimolo
PS : Gwen tu as la bonne borne du rapport entre les deux gâteaux , n'oublie pas que ce rapport doit être rationnel et supérieur à 1 .
PPS : Unecoudée : il te reste une paire de gâteau à trouver .
#10 - 27-12-2014 10:40:58
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâteau 8
Sauf erreur, j'en trouve 13 et aucune ne correspond à l'énoncé.
64 96 144 216 760
56 84 126 189 665
48 72 108 162 570
64 80 100 125 549
54 72 96 128 518
40 60 90 135 475
32 48 72 108 380
24 36 54 81 285
27 36 48 64 259
16 24 36 54 190
8 12 18 27 95
2 4 8 16 42
1 2 4 8 21
#11 - 27-12-2014 11:13:54
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gteau 86
j'ai une somme de 392 mais pas de triangle constructible avec: 27 , 45 , 75 & 125 et le rapport: 5/3 > nb d'or 1.6180339...
#12 - 27-12-2014 11:28:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#13 - 27-12-2014 12:44:13
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
gâyeau 86
Bah ce sont a, b, c, d et la longueur totale.
#14 - 27-12-2014 12:48:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâtrau 86
Tu me montres un triangle 1 2 4 
Vasimolo
#15 - 27-12-2014 13:35:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gâteau 6
@Tous : ceux qui ont suivi du coin de l’œil les péripéties de mon pâtissier savent que le mensonge ne lui fait pas peur mais qu'alors il faut lui faire entendre raison autrement qu'avec un argument du style : "j'ai tout essayé et il n'y a rien qui marche"
Bon, je préfère ça....
L'équation de toutes lee données du problème se résume par
390<a(1+2k+2k²+k^3)<400 avec k<nb d'or et a,ka,ka²,k^3*a entiers.
On pose k=p/q. il faut a=a'q^3.
390<a'(q^3+2pq²+2p²q+p^3) avec p>q
Pour p=q, limite inf----->6q^3<400 donc q<5
ça ne marche pas avec q=2 (3/2) q=3(4/3) q=4(5/4).
il n'y a pas de solution.
#16 - 27-12-2014 17:13:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtea u86
C'est ça Nodgim 
Avec une minoration plus fine tu peux même te limiter à q<4 .
Vasimolo
#17 - 27-12-2014 18:22:21
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3523
- Lieu: 94110
Gâetau 86
Après une petite réflexion, on s'aperçoit que les relations entre les cotés des triangles imposent que :
A soit de la forme i*n^3,
B de la forme i*n^2*m,
C de la forme i*n*m^2,
et D de la forme i*m^3.
Il ne reste plus beaucoup de solutions à tester pour trouver i, n et m.
1er essai :
Avec i= 1, n= 3 et m = 5, on obtient:
A = 27, B = 45, C= 75 et D = 125, soit L = 392 cm.
mais on ne respecte pas l'inégalité triangulaire : A+B = 72 < C 
2ème essai :
Avec i= 4, n= 2 et m = 3, on obtient:
A = 32, B = 48, C= 72 et D = 108, soit L = 380 cm.
L'inégalité triangulaire est bien respectée mais il reste plus de 10 cm ...  
3ème essai :
Avec i= 2, n= 3 et m = 4, on obtient:
A = 54, B = 72, C= 96 et D = 128, soit L = 518 cm.
L'inégalité triangulaire est bien respectée mais les 4 m de ruban sont loin de suffire ...   
Ton pâtissier se serait-il moqué de toi  , ou bien serais-je passé à coté de quelque chose ??? , ou bien serais-je passé à coté de quelque chose ??? 
#18 - 27-12-2014 18:47:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#19 - 27-12-2014 19:14:45
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gâteaau 86
Est-ce qu'il existe une solution?
Un promath- actif dans un forum actif
#20 - 27-12-2014 19:16:04
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
gâteai 86
Un promath- actif dans un forum actif
#21 - 27-12-2014 19:20:12
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
gâyeau 86
A cause de l'inégalité triangulaire, je n'ai trouvé que les triangles équilatéraux de côtés 65 et 66.
#22 - 27-12-2014 19:23:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtaeu 86
@Promath : j'ai corrigé ( je me suis embêté avec les caractères spéciaux de windows et j'ai mélangé a et k  ) )
@Halloduda : non 
Vasimolo
#23 - 27-12-2014 19:46:52
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
âGteau 86
Est-ce qu'il existe une solution?
Soit k=b/a=c/b=d/c
On majore k.
Selon l'inégalité triangulaire, c<a+b donc k²a<ka+a donc k<PHI (trivial)
Selon la découpe, a+2ka+2k²a+k^3<400 mais c'est en même temps supérieur à 390. On simplifie tout ça!
390<a(k+1)*(k²+k+1)<400
On note k=p/q irréductible. Donc q^3 divise a, on note d'ailleurs a=q^3*m avec m entier aussi.
Ainsi 390<m(p+q)(p+q+1)(p+q-1)<400 après une très lourde simplification
On cherche un nombre compris entre 390 et 400 multiple de 6.
396 est le seul.
396=2²*3²*11
On fait ressortir le m=11 car 10 et 13 ne sont pas atteignables par les facteurs premiers de 396
d'où (p+q)(p+q-1)(p+q+1)=36 et on voit très vite que c'est impossible.
Donc il n'existe aucune solution
Edit: d'ailleurs c'est facile à vérifier, on a soit k=3/2 ce qui débouche sur 4 cas avec a=8m,m<->[1;4] ou k=4/3 avec a=27 mais les cas ne marchent pas
Un promath- actif dans un forum actif
#24 - 27-12-2014 21:21:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteeau 86
Oui Promath- 
Vasimolo
#25 - 27-12-2014 21:36:24
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gteau 86
Oui c'est bon ou oui il y a une solution?
Un promath- actif dans un forum actif
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum