 |
#1 - 11-02-2015 14:02:38
- DeepSpidou2.5
- Habitué de Prise2Tete
- Enigmes résolues : 30
- Messages : 49
Gontrand Azerty de Yuio
Bonjour, bonjour !
Extrait de "Exercices ordinaires de Probabilités" - Gérard Frugier :
Gontrand Azerty de Yuiop est le dernier du nom. Il vient d'épouser Marie-Chantal qui lui donnera trois enfants. Sachant que tous les descendants auront trois enfants, calculer la probabilité pour que le nom Azerty de Yuiop disparaisse.
(Sous-entendant que les garçons garderont ce nom tandis que les filles le perdront)
La case réponse valide le résultat à 10−3 près.
Bon Courage ! 
#2 - 11-02-2015 16:47:34
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gontrand Azerty ed Yuiop
Bonjour,
Soit P la probabilité que le nom s'éteigne pour un garçon (elle est de 1 pour une fille).
Le couple initial peut avoir :
3 filles, avec une probabilité 1/8 => probabilté d'extinction = 1*1*1
2 filles, avec une probabilité 3/8 => probabilté d'extinction = 1*1*P
1 fille, avec une probabilité 3/8 => probabilté d'extinction = 1*P*P
0 fille, avec une probabilité 1/8 => probabilté d'extinction = P*P*P
D'où
On obtient l'équation du 3ème degré
La valeur à conserver est la racine positive de l'équation du second degré
P = sqrt(5) - 2 = 0.236
#3 - 11-02-2015 19:44:15
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gontrand Azerty de Yuio
J'aurais dit 1/7 après observation de l'arbre des probas. Mais ça ne valide pas.
#4 - 11-02-2015 20:13:52
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Gontrand Azerty d Yuiop
Et j'ai fait ce dont je suis amateur, des petits codes qui donnent des résultats statistiques approchés 
le pourcentage recherché est de 0.2360359 pour 7 millions de cas testés 
#5 - 11-02-2015 21:55:40
- DeepSpidou2.5
- Habitué de Prise2Tete
- Enigmes résolues : 30
- Messages : 49
Gonrand Azerty de Yuiop
@enigmatus : Et bien c'est (presque) parfait ! 
Il aurait juste fallu rapidement justifier pourquoi ta valeur est le bon résultat, et pas P=1, valeur qui annule aussi ton expression !
@nodgim : Je ne sais pas trop d'où sort ta valeur ^^'
@kossi : Que répondre à ça ! 
En effet la réponse est la bonne, ton code est efficace, mais le pourquoi reste intéressant !
#6 - 12-02-2015 09:07:45
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gontrand Azerty de Yuuiop
DeepSpidou2.5 #5 a écrit:Il aurait juste fallu rapidement justifier pourquoi ta valeur est le bon résultat, et pas P=1, valeur qui annule aussi ton expression !
Parce qu'elle ne valide pas la case réponse… 
On peut concevoir en effet que le nom disparaisse systématiquement à long terme, et je ne vois pas de raison de choisir une valeur plutôt que l'autre. Pourtant la probabilité d'extinction doit être unique…
Ajouté :
Si on part de cette équation (voir #2)
et qu'on la résoud de façon itérative (en partant d'une valeur 0 ≤ P0 < 1, et en calculant P = 1/8*1 + 3/8*P0 + 3/8*P0^2 + 1/8*P0^3, qu'on reporte ensuite dans le membre de droite), c'est vers la valeur 0.236 que l'on converge.
Généralisation :
Pour 1 seul enfant par famille : P = 1 est racine simple
Pour 2 enfants par famille : P = 1 est racine double
Pour 3 enfants par famille : P = 1 et P = 0.236 sont les 2 racines positives
Pour 4 enfants par famille : P = 1 et P = 0.0874 sont les 2 racines réelles
#7 - 12-02-2015 16:28:25
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Gontrand Azerty de YYuiop
P = 1/8 + 3/8*P + 3/8*P² + 1/8*P^3
donne (P-1)(P²+4P-1) = 0
donc P=1 ou P=rac(5)-2
Je pense que P ne vaut pas 1, mais je n'ai pas encore trouvé pourquoi
#8 - 12-02-2015 17:50:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gontrand azerty dr yuiop
Bonsoir
Je trouve √5−2
Le calcul est simple si on le prend par le bon bout ( c'est à dire à l'envers  ) . ) .
On ne considère que les mâles de la famille . La probabilité que la descendance d'un mâle s'éteigne est la même pour chacun , on la note P . On part d'un mâle quelconque E1 et on regarde la probabilité pour que sa descendance s'éteigne .
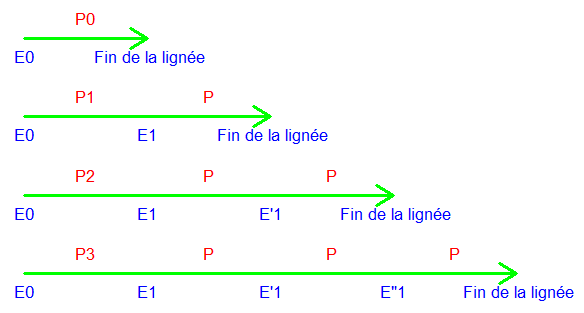
P0=1/8 , P1=3/8 , P2=3/8 , P3=1/8 est la probabilité pour qu'il ait 0 , 1 , 2 , 3 enfants mâles .
On note ensuite E0 le père de E1 . La probabilité pour que la descendance de E0 s'éteigne est P-1/8 .
On a donc 3P/8+3P²/8+P³/8=P-1/8 donc P³+3P²-5P+1=0 .
Vasimolo
#9 - 12-02-2015 18:14:02
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
gontranf azerty de yuiop
J'ai trouvé pourquoi P ne peut être égal à 1.
On note P(n) la proba que le nom ait disparu au bout de n générations
Alors P = lim P(n)
On a P(n+1) = 1/8 + 3/8*P(n) + 3/8*P(n)² + 1/8*P(n)^3
On note a = rac(5)-2
et f la fonction définie par f(x) = 1/8 + 3/8*x + 3/8*x² + 1/8*x^3
Remarque : f(a) = a (cf message précédent)
La fonction f est croissante sur l'ensemble des réels positifs, comme somme de fonctions croissantes.
Par récurrence, on prouve alors que que 0 <= P(n) <= a :
Initialisation : P(0) = 0 donc 0 <= P(0) <= a
Hérédité : Si 0 <= P(n) <= a alors par croissance de f sur R+,
f(0) <= f(P(n)) <= f(a) donc 0 <= P(n+1) <= a
Par conséquent, P(n) <= a pour tout n, et donc P <= a.
CQFD
#10 - 14-02-2015 15:52:17
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
ontrand Azerty de Yuiop
Soit p la probabilité cherchée d'extinction du nom pour la descendance d'un mâle Azerty.
On va supposer une répartition des naissances filles / garçons et une longévité de tous les descendants leur assurant leur 3 enfants, ni plus, ni moins !
4 cas sont possibles pour la première génération :
3 garçons (1 chance sur 8)
3 filles (1 malchance sur 8)
2 garçons et 1 fille et 1 garçon et 2 filles se partagent par symétrie les chances restantes : 3/8 chacun.
Chaque fille porte une proba d'extinction de 1 et chaque garçon de p, donc la proba d'extinction vue à la première génération est : p^3/8 + 3p^2/8+3p/8+1.
En égalisant les 2 probas (génération 0 et génération 1); on obtient
p = p^3/8 + 3p^2/8+3p/8+1/8
d'où p^3 + 3p^2 - 5p + 1 = 0
1 est racine "évidente", et on résout p²+4p-1=0 pour trouver les 3 racines :
p0=1
p1=-2-rac(5)
p2=-2+rac(5)
p1 est en dehors de de [0;1]
je ne trouve pas d'argumentation évidente et rapide pour dire que p0=1 n'est pas la solution (ça correspond à la valeur cherchée si en génération 0 on a une fille et pas un garçon...)
La réponse valide restante est donc p2~0,236
#11 - 14-02-2015 19:20:18
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gontrrand Azerty de Yuiop
Fainéant et optimiste comme je suis, j'aurais dit 100%. Après un temps infini, cela ne devrait-il pas arriver ?
Les calculs me semblent vite fastidieux. 1/8 à la première génération...
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#12 - 14-02-2015 19:57:24
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
gonttand azerty de yuiop
Probabilité d'avoir trois filles (mais aucun garçon) à la génération suivante
= FFF = 1/8
Probabilité d'avoir deux filles (et un seul garçon) à la génération suivante
= FFG+FGF+GFF = 3/8
Probabilité d'avoir une seule fille (et deux garçons) à la génération suivante
= FGG+GFG+GGF = 3/8
Probabilité de n'avoir aucune fille (mais trois garçons) à la génération suivante
= GGG = 1/8
Probabilité que le nom disparaisse
= (1/8) x 1 + (3/8) x [(1/3) x (1/8) + (2/3) x 1] + (3/8) x [(2/3) x (1/8²) + (1/3) x 1] + (1/8) x (1/8³) = 2129 / 4096 = env. 0,51977
Mais ni 0,519; ni 0,520; ni 0,52; ni 0.519; ni 0.520; ni 0.52 ne sont validés.
J’ai dû faire une erreur de raisonnement quelque part. Affaire à suivre …
#13 - 16-02-2015 13:44:37
- DeepSpidou2.5
- Habitué de Prise2Tete
- Enigmes résolues : 30
- Messages : 49
gontrand azerty de yyiop
@enigmatus : Voilà, c'est parfait ! 
@titoufred : En effet, c'est bien ça, mais pour trouver laquelle est la bonne, il faut jeter un coup d'oeil à la relation de récurrence qui est sous-entendue dans ton raisonnement !
EDIT : T'as pensé à ça, je retire, BRAVO ! 
@Vasimolo : Comme tout le monde, avec ton expression, il semble que P=1 fonctionne aussi alors, non ? 
@dylasse : Pour éliminer 1, il faut étudier la récurrence de ton raisonnement, peut-être faire une étude de fonction pour voir que 1 n'est pas possible, toussa, toussa... 
@fix33 : En première lecture, c'est ce que j'ai pensé aussi ! Mais quelle ne fut pas ma surprise de trouver une valeur bien différente après une étude (pas si longue  ) du problème. ) du problème.
@Franky1103 : L'énoncé était peut-être ambigu, mais ils n'arrêtent pas de faire des enfants après la première génération ! 
Ils continuent encore, et encore, et encooore, et on voudrait savoir vers quoi va tendre la probabilité que le nom s'éteigne.
#14 - 16-02-2015 13:53:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gontrand azeryy de yuiop
Bien sûr que p=1 fonctionne et avec p=i on se poserait la question ?
Vasimolo
#15 - 17-02-2015 11:17:14
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Gontrand Azerty de Yuioop
Je me suis effectivement bêtement arrêté au bout de deux générations.
En passant d'une génération à la suivante:
- Probabilité d'avoir trois filles (mais aucun garçon) = FFF = 1/8,
- Probabilité d'avoir deux filles (et un seul garçon) = FFG+FGF+GFF = 3/8,
- Probabilité d'avoir une seule fille (et deux garçons) = FGG+GFG+GGF = 3/8,
- Probabilité de n'avoir aucune fille (mais trois garçons) = GGG = 1/8.
J’appelle P la probabilité que le nom disparaisse. J’aurai:
P = (1/8).1 + (3/8).[(1/3).P + (2/3).1] + (3/8).{(2/3).[1-(1-P)²] + (1/3).1}
+ (1/8).[1-(1-P)³]
Après simplification, j’aurai: P³-5.P²+4 = 0, soit: (P-1).(P²-4.P-4) = 0
J’aurai alors: P = 2.(1+V2), rejetée car >1; ou: P = 2.(1-V2), rejetée car <0; ou:
P = 1
Je serai donc certain que le nom disparaisse, mais cette réponse n'est pas validée.
J’ai encore dû faire une erreur de raisonnement quelque part. Affaire à suivre …
Edit: Maintenant que le masque est levé, je vois où est mon erreur: j'aurais dû multiplier les probabilités de deux évènements indépendants, comme on le fait traditionnellement.

#16 - 17-02-2015 18:35:45
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gontrand Azerty ed Yuiop
Malheureusement pas le temps ni l'énergie pour chercher. Le résultat est certainement compris entre 1/8 et 1/2. 1/8 s'ils n'ont que des filles. 1/2 parce que en moyenne, il y aura 1,5 garçon par couple, dont les puissances tendent vers l'infini, mais c'est sans aucun doute un mauvais raisonnement !
Je suis curieux de voir la réponse et les raisonnements.
Avec 2 enfants ou moins la réponse est 100% !
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#17 - 18-02-2015 23:30:19
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Gontrand Azerty de YYuiop
Bonsoir,
Il y a un truc qui m'échappe. Quand je prends l'explication de Titou, tout est nickel sauf que je ne vois pas d'où vient : On a P(n+1) = 1/8 + 3/8*P(n) + 3/8*P(n)² + 1/8*P(n)^3
Je ne vois pas comment est pris en compte le nombre de mâles AZERTY de la génération n pour établir cette relation de récurrence, et pourtant ce nombre me semble influant (pour une même probabilité de non extinction à la génération n (1-P(n)), ce n'est pas la même chose d'avoir un seul mâle AZERTY ou un très grand nombre à cette génération n pour calculer la probabilité d'extinction à la génération suivante).
A la génération 2, on a déjà 9 enfants de 3 types possibles : mâles AZERTY, mâles non AZERTY et filles, et le décompte des possibilités est déjà très lourd.
Merci de m'éclairer sur l'origine, a priori évidente, de la relation de récurrence. Je ne dois pas regarder par le bon bout !
#18 - 19-02-2015 06:32:19
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gontrand Azerty d eYuiop
Bonjour dylasse,
P(n) et P(n+1) ne sont pas relatifs à deux générations différentes, mais à deux étapes successives de la résolution itérative de l'équation. Les quatre termes du membre de droite correspondent respectivement aux probabilités d'extinction selon que les 3 enfants d'une famille contiennent 0, 1, 2 ou 3 garçons.
#19 - 19-02-2015 11:43:15
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Gontrandd Azerty de Yuiop
Vasimolo a écrit:Bien sûr que p=1 fonctionne et avec p=i on se poserait la question ?
Vasimolo
Que veux-tu dire par là Vasimolo ? C'est évident que p=1 ne peut pas convenir pour toi ?
@dylasse : je note P(n) la probabilité que le nom ait disparu au bout de n générations au maximum. Après, on raisonne juste sur le nombre de garçons de Gontrand pour établir l'égalité avec P(n+1) : il a une proba 1/8 d'avoir 0 garçon et le nom disparait, proba 3/8 d'avoir un garçon et le nom disparait avec une proba P(n), ...., proba 1/8 d'avoir 3 garçons et le nom disparait avec une proba P(n) pour chacune des 3 lignées donc avec une proba P(n)^3 pour toutes les 3.
#20 - 19-02-2015 17:19:37
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gonttand azerty de yuiop
Le cas P=1 m'a semblé tout de suite à écarter car à chaque génération le nombre moyen de garçons de la lignée est multiplié par 1,5 . Le risque d'extinction va donc en diminuant à chaque génération . Comme il n'est déjà pas très élevé au départ ...
Je sais que ce n'est pas très formel mais j'arrive à m'en satisfaire 
Vasimolo
#21 - 20-02-2015 11:01:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gontrand Azerty ed Yuiop
La recherche de la proba conduit à une équation. La résolution de l'équation ne conduit pas tjs à des solutions en rapport avec le problème. De même que P=1 est écarté par une raison de bon sens, de même la racine négative n'est pas retenue. Quelle serait ici la réalité de la racine négative ? Dans ce problème, on cherche une proba comprise entre 0 et 1, pas la proba 1. On pourrait l'écrire par avance dans l'intervalle des solutions possibles pour lever toute ambiguïté. Je crois que ça ne choquerait personne. C'est l'inverse qui serait difficile à soutenir.
#22 - 20-02-2015 11:06:48
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gontrand Azerty de Yiuop
C'est bizarre mais si j'applique la même méthode avec 2 enfants au lieu de 3, j'aboutit à l'équation:
4p=1+2p+p²
p²-2p+1=0
(p-1)²=0
p=1
Où est l'erreur ?
#23 - 20-02-2015 12:25:44
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Gontrand Azrty de Yuiop
Il n'y a pas d'erreur, la proba cherchée P est une limite de probas P(n) lorsque le nombre n de générations tend vers l'infini. Même si P(n)<1, la proba P=1 n'est pas du tout à écarter d'entrée. Avec 2 enfants, le nom va disparaitre de façon (quasi-)certaine avec le temps.
@Vasimolo : L'argument avec le nombre moyen de garçons ne suffit pas selon moi.
#24 - 20-02-2015 12:59:49
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gontrrand Azerty de Yuiop
Pour les 2 enfants, c'est un résultat étonnant. Pour 3 enfants, le fait qu'il n'y ait qu'une seule proba possible n'est il pas suffisant ? Et choisir entre 1 et 0,236, le choix n'est il pas évident ?
#25 - 20-02-2015 14:04:27
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
gontrand azertt de yuiop
Rien que le fait de te poser la question "le choix n'est-il pas évident ?" apporte la réponse à ta question.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







