|
#26 - 29-12-2015 14:35:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
âteau 116
Bon je crois que j'ai.
On peut toujours construire une boucle entre 2 segments. Démontrons qu'on peut modifier si nécessaire cette boucle au minimum et de façon systématique, pour prendre en charge un nouveau segment.
Pour ce faire, il y a une précaution à prendre: on choisit au départ le segment S1 au hasard et le segment S2 est un de ceux dont l'extrémité Ep la plus proche de S1 est telle qu'il n'y a aucune autre extrémité dans le triangle S1-Ep. On colorie ce triangle. Pour le choix de S3, on procède de même: entre l'extrémité de S3 la plus proche du triangle coloriée et la face correspondante du triangle colorié, ça doit être vierge de toute autre extrémité. On colorie ce nouveau triangle, et on procéde ainsi pour tous les nouveaux segments incorporés. Cette précaution garantit que toute nouvelle extrémité ne pourra au pire que couper une seule fois la boucle.
Après le choix des 2 segments de départ, on établit une boucle et on a un réseau. On incorpore au réseau le segment S3 et 3 cas se présentent:
-S3 coupe la boucle: la boucle est déviée pour prendre en série ce nouveau segment.
-S3 ne coupe pas la boucle: On la dévie également pour l'incorporer.
-S3 fait face à un segment Sp et non pas à une face de la zone coloriée : c'est le cas particulier du bug signalé au tout début. On est dans le cas d'un réseau indépendant, on relie le segment nouveau aux extrémités du segment Sp et on colorie le triangle correspondant.
Même procédé pour S4, S5, et tous les autres segments.
A la fin, on est sûr d'avoir un réseau bouclé.
#27 - 29-12-2015 14:39:36
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
Gâteau 16
Je pense que le plus simple est d'enfermer les segments dans un polygone convexe puis de trianguler sa surface.
Tout noeud peut être relié à "l'extérieur". Ca fait des formes bizarres mais ça marche.
#28 - 29-12-2015 16:41:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtau 116
@Nodgim & Gwen : il est difficile de comprendre vos démonstrations .
Mais Je suis certain qu'elles sont fausses car j'ai un contre-exemple sous les yeux 
Vasimolo
PS : j'ajoute un peu de temps et je donnerai quelques indices si personne ne trouve .
#29 - 29-12-2015 16:55:44
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
gâteai 116
@vasimolo
Ton dernier message sous entend qu'il existe des configurations impossibles ou j'extrapole ? Tant qu'à chercher, autant chercher dans la bonne direction, non ?..
#30 - 29-12-2015 16:57:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâteai 116
@Portugal : ce n'est pas un sous-entendu 
Vasimolo
#31 - 29-12-2015 17:04:57
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gââteau 116
 
Ça change la façon d’appréhender le problème en effet...
#32 - 29-12-2015 17:38:54
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
Gâteau 161
Le plus simple serait de laisser le temps et de balancer ton contre-exemple... pour voir s'il est convaincant 
#33 - 29-12-2015 17:43:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#34 - 29-12-2015 18:29:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 11
Je viens de recevoir du site , le message suivant :
Voilà 72h que ton énigme Gâteau 116 a été proposée sur le forum de Prise2Tete.
Ton sujet à reçu 7 réponse(s), et celles-ci sont désormais visibles de tous. Tu peux à présent poster la réponse (si tu la connais) et féliciter les joueurs ayant trouvé une réponse correcte si ce n'est pas déjà fait.
Merci.
C'est marrant , ça doit être une réponse au premier problème ( assez pourri ) que j'avais proposé . Le site garde donc souvenir des problèmes effacés 
D'un autre côté si l'énigme est devenue trop agaçante ou si chacun préfère partager ses idées avec les autres : je lève le masque ( je n'aime pas trop les bals masqués qui s'éternisent ) .
Vasimolo
PS : j'ai encore quelques indices en réserve 
#35 - 29-12-2015 18:48:11
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
Gâteau 16
j'ai encore quelques indices en réserve
Parce que tu en as déjà donné ? 
Chercher une preuve était plaisant, fouiller pour un contre-exemple ne m'intéresse pas, personnellement. J'ai testé quelques situations a-priori bloquantes et au bout du compte, j'ai trouvé une solution pour chacune.
#36 - 29-12-2015 18:51:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 11
Ben Gwen , j'ai dit qu'il y avait un contre-exemple , c'est un indice énorme .
Vasimolo
#37 - 29-12-2015 18:55:38
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
Gâtteau 116
Bah ça me permet de répondre à la question (sur tes dires) : NON
Mais comme en cherchant une preuve on la met à l'épreuve des contre-exemples, ça veut dire que j'en ai cherché sans en trouver.
Je ne vois pas ce qui pourrait empêcher de relier ces segments.
#38 - 29-12-2015 22:59:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gteau 116
J'ai été bluffé aussi et pourtant la solution est assez simple mais je n'en dis pas plus , je donnerai d'autres indices plus tard si personne ne trouve avant 
Vasimolo
#39 - 29-12-2015 23:14:13
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
#40 - 29-12-2015 23:23:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#41 - 29-12-2015 23:35:54
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
gâteai 116
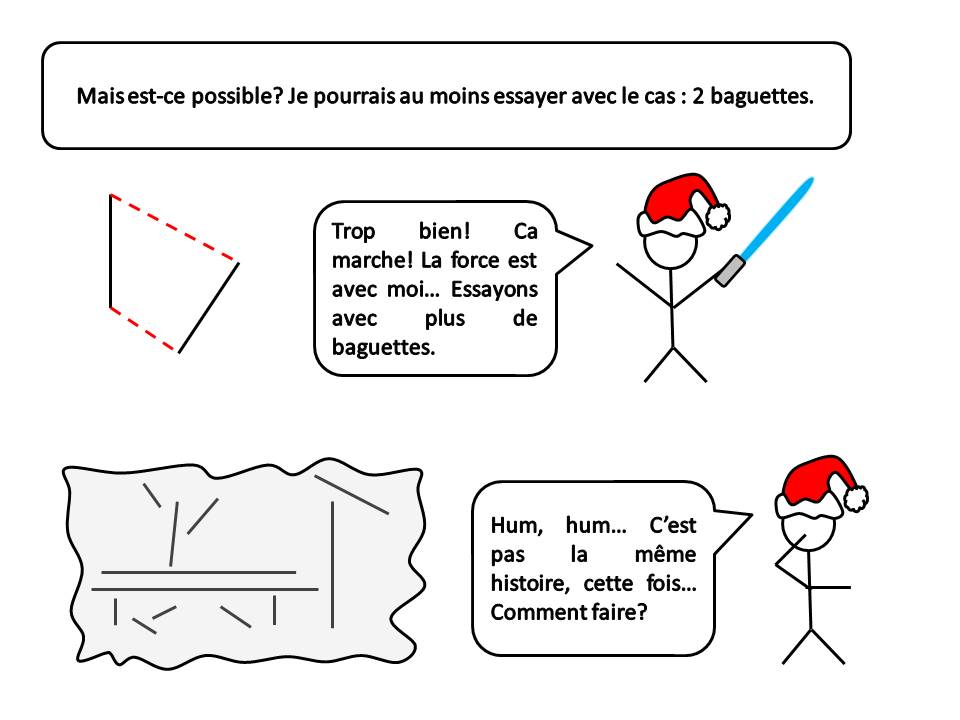
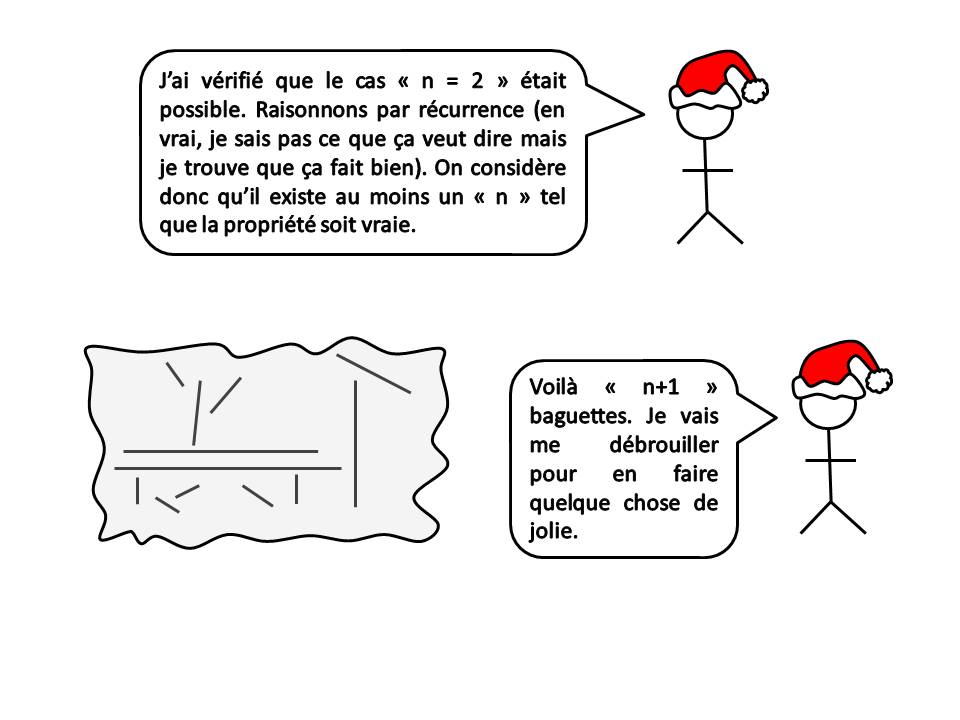
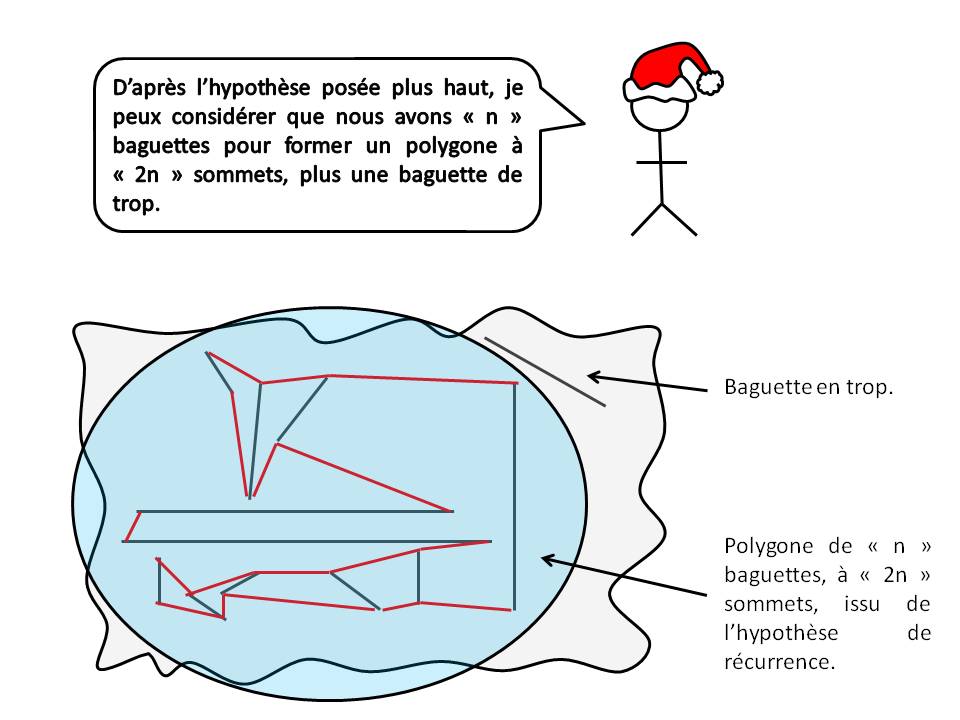
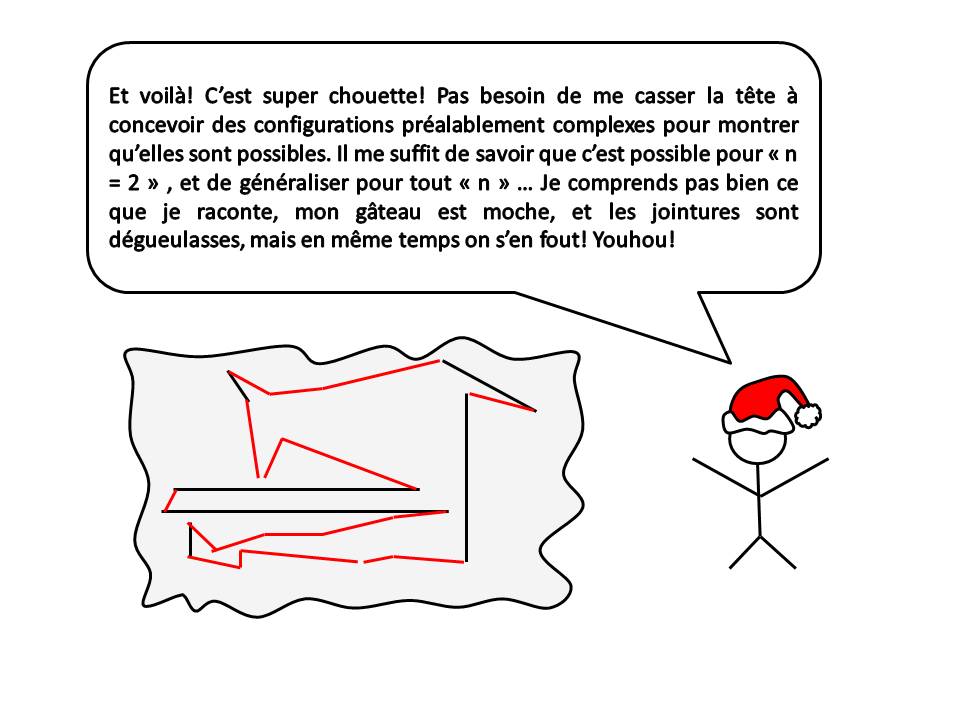
Un contre-exemple? Intéressant. Il y a donc une configuration gênante pour relier le polygone à " 2n " sommets, avec la nouvelle baguette. C'est ce que je craignais dans ma démonstration : suivant l'orientation de la " n+1 " ème baguette, on peut se heurter à certaine impossibilité... Pour l'instant, je ne vois pas, mais je continue à chercher. Problème très intéressant en tout cas. 
#42 - 30-12-2015 09:41:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâetau 116
Bon j'ai trouvé le bug dans ma démo, c'est déja ça. Malheureusement, ça ne m'aide pas pour trouver le contre exemple...
#43 - 30-12-2015 10:18:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
âteau 116
Je donne un deuxième indice : il y a un contre-exemple avec 6 baguettes .
Bonne recherche 
Vasimolo
#44 - 31-12-2015 10:08:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
âteau 116
Troisième indice : il y a un contre-exemple avec un axe de symétrie .
Vasimolo
#45 - 31-12-2015 11:14:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteaau 116
Axe de symétrie avec 6 segments ?
J'ai essayé au pif: une spirale base carrée ou base triangulaire: rien.
Et des tas de config + ou - au hasard en limitant au max les choix possibles quand on est à une extrémité.
Cette enigme est diabolique. On dirait un ruban de Moebius, mais en 2D.
#46 - 31-12-2015 12:15:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteaau 116
Ce n'est pas si compliqué Nodgim , il faut garder à l'esprit la rigidité des baguettes 
L'énigme n'entre absolument pas dans la théorie des graphes ou de la topologie .
Vasimolo
PS : je déconne mais la solution est assez bluffante , la réponse l'année prochaine ????
#47 - 01-01-2016 18:09:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtea u116
Nouvel indice : une des baguettes est incluse dans l'axe de symétrie .
Vasimolo
#48 - 01-01-2016 18:40:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
gâtrau 116
Perso j'attends la soluce, et elle doit être vicieuse.
On peut modéliser un segment par un double noeud (2 bulles appariées), ça libère les contraintes des segments rectilignes, le graphe est plus traditionnel. J'en ai déduit que, hormis le cas d'un long segment qui viendrait couper le réseau en 2 réseaux distincts, chaque bulle est en contact avec au moins 2 autres bulles de paires distinctes, et plus souvent 3. En réalisant le graphe de qq cas, on constate que le nb de liaisons est important. Je suis impatient de voir la soluce pour reconstituer le graphe correspondant.
Un segment dans l'axe de symétrie, alors c'est pour une solution avec 7 segments ?
#49 - 01-01-2016 18:50:32
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâetau 116
Avec le dernier indice que tu donnes, je suis de plus en plus surpris. Quelque chose m'échappe complètement. Avec la baguette dans l'axe, j'ai vraiment du mal à imaginer le truc. Mettons que j'arrive à faire une boucle avec la partie droite, il n'y aucune raison de ne pas pouvoir le faire avec la partie gauche. D'autant que la baguette dans l'axe peut être en parallèle de la boucle, et non en série.
#50 - 01-01-2016 18:54:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteauu 116
La solution n'a rien de tordu Nodgim , il faut oublier les graphes et la topologie et se souvenir qu'on travaille sur des segments qui sont par nature rigides et limités .
Je donnerai demain un dernier indice qui devrait faire tilt pour beaucoup .
En tout cas , bonne année à toi et à tout le forum 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum