 |
#26 - 09-01-2016 09:21:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâteai 117
Tu as presque tout dit , il manque juste un petit élément .
Vasimolo
#27 - 09-01-2016 09:30:06
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâeau 117
Suite du #5 :
La probabilité cherchée est 10.9375 % = 726.
Raisonnement :
On place les points sur un cercle de longueur 1. La somme des distances entre les points est donc 1.
On considère ces valeurs comme les coordonnées barycentriques d'un point dans l'équivalent d'un tétraèdre dans un espace à (P-1) dimensions (P est le nombre de points).
On s'intéresse aux points dont une des coordonnées barycentriques est supérieure à 1/2.
P=3
On a un triangle T, subdivisé en 4 triangles de côté de longueur moitié de T.
On s'intéresse aux points situés dans les triangles jouxtant les 3 sommets de T.
P=4
On a un tétraèdre T, subdivisé en 8 tétraèdres de côté de longueur moitié de T.
On s'intéresse aux points situés dans les tétraèdres jouxtant les 4 sommets de T.
..................................................................................
P=n
On a un hyper-tétraèdre T, subdivisé en 2n−1 hyper-tétraèdres de côté de longueur moitié de T.
On s'intéresse aux points situés dans les hyper-tétraèdres jouxtant les n sommets de T.
#28 - 09-01-2016 09:30:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteau 1177
La réponse à la question est non, il y a plus de 10% de chance d'enlever la fève au centre, car la proba est 7/2^6, et si on avait n fèves, ce serait n/2^(n-1).
Si on considère n pts pris au hasard, aucun diamétralement opposé deux à deux, ce qui est tjs le cas quand on prend les points au hasard, alors on peut tjs reporter les n pts d'un coté du gâteau selon un diamètre pris au hasard en déplaçant certains pts vers leurs opposés diamétraux. Dans ce cas, le polygone ne passe plus par le centre. Et si on déplace l'un des 2 pts extrêmes du groupe de pts, le nouveau polygone est également hors centre. En revanche si on déplace l'un des pts intermédiaires, le polygone englobe le centre. Si on fait le bilan de ttes les configs possibles, il n'y a que 2n polygones hors centre sur les 2^n polygones possibles.
P=0,109375.
#29 - 09-01-2016 10:32:00
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
gâteay 117
J'obtiens bien une probabilité précise mais visiblement fausse. Je vais développer mon raisonnement pour que l'on puisse m'expliquer ou est l'erreur :
On considère les sommets disjoints 2 à 2 ( les autres cas sont de probabilité nulle)
Événement i : "Il y a un demi cercle vide à gauche du sommet i"
Comme il ne peut pas y avoir 2 demi-cercles vides, les événement i sont disjoints
Donc proba " il existe un demi cercle vide " = somme des proba des événements i
On a donc Proba (pas de fève) = 7 / (2^6) = 10.9375%
#30 - 09-01-2016 10:57:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteeau 117
@Enigmatus : quelle distance utilises-tu pour que la somme des distances soit égale à 1 ?
@Nodgim : Non mais le point de départ est bon .
@Portugal : c'est bon 
Vasimolo
#31 - 09-01-2016 11:14:36
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
gâteay 117
Exact, j'ai mal compté mes polygones hors centre. Il y en a 2n et non n dans un tour complet, et donc la formule générale est n/2^(n-1), et pour n=7 P=0,109375.
#32 - 09-01-2016 11:25:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtteau 117
C'est ça 
Vasimolo
#33 - 09-01-2016 11:44:28
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteua 117
Vasimolo #30 a écrit:@Enigmatus : quelle distance utilises-tu pour que la somme des distances soit égale à 1 ?
Je place les points sur une circonférence de longueur 1, ce qui entraîne que la somme des distances entre les points vaut également 1.
Ce qui me semble moins acquis, c'est que la probabilité des répartitions soit proportionnelle à l'aire occupée par le point représentatif dans le triangle (pour 3 points), le volume (pour 4 points), ou l'hyper-volume.
#34 - 09-01-2016 11:50:56
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâtteau 117
Ce qui est étonnant, c'est que j'ai fait la même erreur dans l'autre méthode, qui a aussi amené à un résultat moitié de l'attendu. En découpant en 8 secteurs, le résultat donne 0,1092300415, pour 0,109375, ce qui est plutôt proche de la solution !
#35 - 09-01-2016 11:54:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 1117
enigmatus a écrit:Je place les points sur une circonférence de longueur 1, ce qui entraîne que la somme des distances entre les points vaut également 1.
Il me semble que non 
Vasimolo
#36 - 09-01-2016 12:48:36
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteau 1117
Vasimolo #35 a écrit:Il me semble que non
Je parle de la somme des distances en prenant les points consécutifs 2 à 2 :
1->2, 2->3, ..., (n-1)->n, n->1
#37 - 09-01-2016 12:51:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâtezu 117
C'est bien ce que j'avais compris mais ça ne marche pas 
Vasimolo
#38 - 09-01-2016 13:01:15
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteau 11
Je ne vois vraiment pas ce que tu veux dire… La circonférence a une longueur de 1, on en fait le tour et on revient au point de départ, on a bien parcouru une longueur de 1 ?
#39 - 09-01-2016 14:30:15
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gâtea u117
Quelques remarques.
La formule générale est
Proba(n)= n/(2^(n-1))
Le résultat est cohérent avec celui trouvé avec lourdeur pour n=3...ouf
De manière amusante ça marche aussi pour 1 et 2
Pour n grand on a
P(n+1)/P(n) tend vers 1/2
Ca s'explique : un demi cercle se remplit au rang n et au rang n+1 il y a une chance sur 2 que le nouveau sommet n'y soit pas.
Enfin on pourrait profiter d'une formule lourde de modélisation du résultat pour utiliser ce modèle pour résoudre une équation complexe...
#40 - 09-01-2016 18:08:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 171
D'accord Eniqmatus , tu suis la circonférence . Pour moi la distance entre deux points A et B c'est la longueur du segment [AB] , c'est pour cette raison que je ne comprenais pas d'où sortait ce 1 . C'est bon 
Vasimolo
#41 - 09-01-2016 19:01:46
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
gâreau 117
Effectivement, pour moi c'était implicite, mais je n'avais pas pensé à le préciser. 
#42 - 09-01-2016 19:16:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 1177
J'avais prévu une petite démonstration , on ne va pas la jeter même s'il y en a plein d'autres au dessus :
On peut supposer sans problème que les points choisis sont distincts et jamais diamétralement opposés . On considère alors un de ces points et le diamètre qu'il génère . Il y a une probabilité de 1/64 pour que les six autres points soient du même côté de ce diamètre .
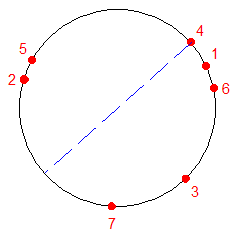
On peut appliquer le même raisonnement à chacun des six autres points . Il n'y a plus qu'à remarquer que les sept événements "les six points sont du même côté du diamètre donné" s'excluent les-uns les autres .
La probabilité pour que les sept points soient dans un même demi-plan et que la fève soient enlevée est donc : 7/64=0,109375 .
Le pâtissier a donc tort 
Merci aux participants et bravo à ceux qui ont trouvé .
Vasimolo
#43 - 09-01-2016 23:00:55
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gâtau 117
Je m’étais bien fait avoir : faisant plus confiance au pâtissier qu'à moi même, je pensais m'être trompé...
Je me méfierai dorénavant de son sens de l'exagération...
L'un des intérêts/difficulté/agacement de tes énigmes est que l'on en sait jamais s'il faut démontrer ou infirmer....C'est a mi chemin entre concevoir un problème et le résoudre...
#44 - 10-01-2016 17:53:35
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
Gâteau 17
Je crois qu'il manque un détail à ta démonstration. Le fait de trouver les 6 autres points du même côté du diamètre est de 1/32 et les 7 événements ne s'excluent pas (entre le premier et le septième point par exemple )
C'est uniquement valable si on tourne dans le même sens à chaque fois et qu'on ne considère qu'un demi-cercle.
#45 - 10-01-2016 18:05:40
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteau 11
En effet , je parcourais implicitement le cercle dans le sens direct et je considérais le demi-cercle qui en résultait .
On ne peut pas tout dire mais il faut en dire assez 
Vasimolo
#46 - 10-01-2016 18:10:16
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteau 1117
Perso, il y a quelque chose qui m'échappe dans la démo type Gwen ou Vasimolo, justement sur cette indépendance. Il y a un raccord intellectuel que je n'arrive pas à faire entre le 1/64 pour 1 point et les 7/64 pour les 7 pts. Et je n'arrive pas à comprendre pourquoi je ne suis pas convaincu.....D'habitude, je hais la formalisation poussée, mais là il me manque qq chose.
#47 - 10-01-2016 18:20:40
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,069E+3
Gâteau 1117
Si tu prends les sept points, il seront sur un même demi-cercle si en partant de l'un de ces points et en parcourant 1/2 cercle tu trouves les six autres.
Si ca ne marche pour aucun des points : c'est fichu.
Maintenant, on a 8 possibilités :
Ca marche pour le point 1
Ca marche pour le point 2
Ca marche pour le point 3
Ca marche pour le point 4
Ca marche pour le point 5
Ca marche pour le point 6
Ca marche pour le point 7
Ca ne marche pas.
Ces huit possibilités couvrent l'ensemble des cas possibles et on ne peut pas en avoir 2 valables en même temps si on garde le même sens de rotation.
La probabilité pour que ça marche est donc la somme de celles des 7 premiers cas de figure.
#48 - 10-01-2016 18:27:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteeau 117
Comme toujours en probabilité c'est un peu difficile à expliquer et il y a des pièges à chaque coin de rue .
Les sept points sont placés au hasard mais une fois pour toute : ils ne bougent plus !!!
On considère un de ces points : la probabilité que les six autres soient dans le demi-cercle suivant ce rayon ( dans le sens direct ) est 1/64 . On peut appliquer le même raisonnement aux six autres points sans rien changer . Comme il est impossible que deux des événements précédents se réalisent en même temps , on peut conclure .
Vasimolo
#49 - 10-01-2016 19:18:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gtâeau 117
Précisément Vasimolo, on étudie la proba avec les 7 pts en place. Si on suppose le cas de 6 pts très groupés, le 7ème aura beaucoup plus de chance de laisser un espace 1/2 que si les 6 premiers pts totalisent presque 1/2. Donc là ça deviendrait très vite compliqué. Donc la question que je me pose, c'est pourquoi on peut affirmer que la position de chaque pt est indépendante des autres. Pour l'instant, ça me heurte un peu.
#50 - 10-01-2016 19:42:02
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
gâtezu 117
Événement i : "Il y a un demi cercle vide à gauche du sommet i"
Comme il ne peut pas y avoir 2 demi-cercles vides, les événement i sont disjoints
Donc proba " il existe un demi cercle vide " = somme des proba des événements i
|
 |

 Accueil
Accueil
 Forum
Forum







