|
#1 - 15-01-2018 18:14:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 15-01-2018 20:36:33
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâteua 149
Tu veux surement dire 2 (au lieu de 20).
#3 - 15-01-2018 21:03:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteauu 149
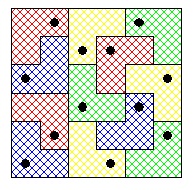
Non , c'est bien 20 , la figure illustre le problème dans une configuration plus simple .
Vasimolo
#4 - 15-01-2018 21:09:13
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
gâteai 149
Heu, si je replique 100 fois ton pavage, je n'ai pas la bonne réponse ?
#5 - 15-01-2018 21:15:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 194
Non , il faut partir d'un pavage quelconque et disposer les pépites ultérieurement , il n' y a aucune raison que le pavage puisse être être séparé en carrés 6 cm X 6 cm .
Vasimolo
#6 - 16-01-2018 09:10:36
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 1149
Ça risque de pas être évident, comme problème.
Première remarque, je ne détaille pas car ce n'est pas très dur à retrouver : ce que tu recherches pour 60x60 et illustres pour 6x6 est envisageable pour tous les rectangles de type (3m)x(3n) (et uniquement ceux-ci), sauf si l'un des deux entiers m, n vaut 1, et l'autre est impair.
Intuitivement, j'aurais tendance à penser que c'est toujours possible, dans la mesure où on a beaucoup de liberté : si, en plaçant une pépite par pièce, les pépites ne sont pas équitablement réparties sur chaque ligne ou colonne, on a, sur chaque pièce, la possibilité de déplacer la pépite d'un cran, ce qui contribue à la changer de ligne mais pas de colonne (ou l'inverse). Après, en tirer une démonstration propre, c'est une autre paire de manches.
Je vais commencer à réfléchir à cela : on place une pépite sur le "coin" de chaque pièce, puis on essaye de démontrer qu'il suffit de déplacer des pépites sans les changer de pièce pour qu'il y ait le même nombre de pépites sur chaque ligne. Si ça marche, on s'inquiètera des colonnes.
#7 - 16-01-2018 13:45:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtrau 149
En effet la condition de pavage d'un rectangle mXn par les triominos en "L" est assez connue : il faut que le nombre de cases soit divisible par 3 et que m et n soient plus grands que 1 voire plus grands que 3 s'ils sont tous les deux impairs . Il me semble que la question du gâteau peut se poser pour tout carré dont le côté est un multiple de 6 . Je suis presque convaincu qu'on peut disposer les pépites comme demandé . On doit même pouvoir choisir 3 couleurs de pépites , poser une pépite par case en équilibrant les couleurs sur chaque ligne et chaque colonne et de façon à ce que chaque pièce contienne une pépite de chaque couleur .
Après il faut le démontrer 
Il doit y avoir une démonstration pas trop compliquée car l'exercice a été proposé à une olympiade ( j'ai simplement changé le côté de 2010 en 60 ) .
Vasimolo
#8 - 16-01-2018 22:37:54
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâtteau 149
On peut se poser la question aussi pour un rectangle (c'était le sens de ma remarque) : par exemple, pour un rectangle de 6 lignes et 3 colonnes, on veut 1 pépite par ligne et 2 pépites par colonne.
Sinon, j'ai un peu progressé. J'arrive à placer facilement une pépite sur chaque pièce de sorte que chaque colonne ait le même nombre de pépites, et j'ai encore de la latitude pour les organiser verticalement. Cette idée va peut-être marcher, affaire à suivre.
#9 - 17-01-2018 08:25:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
GGâteau 149
Peut être en remplissant les cases avec des pépites une diagonale sur 3.
Ensuite, si dans un carré contenant 2 pépites, on se trouve avec 2 pépites dans le même tromino, alors on échange les emplacements entre 2 cases voisines, ce qui garantit l'invariant du nombre de pépites ligne / colonne.
#10 - 17-01-2018 18:22:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteeau 149
@Ebichu : en effet si on regarde uniquement les lignes ou les colonnes on peut ajuster aisément les excès ou les déficits créés par les pépites dans les cases d'angle . Après chaque déplacement "bloque" la pépite qui ne peut plus être utilisée pour l'autre équilibre . On peut toujours dire qu'on avait d'autres choix pour le premier équilibre mais on rentre vite dans une spirale sans fin 
@Nodgim : C'est plutôt malin de remplir les diagonales plutôt que les lignes ou les colonnes et sans s'occuper de la contrainte : une pépite par case . Je suppose qu'après tu pars d'un coin et que tu progresses en diagonale pour équilibrer les pièces . Il faudrait expliquer comment tu de débarrasses des déficits ou des excédents à chaque étape .
J'ai l'impression que l'on progresse 
Vasimolo
#11 - 18-01-2018 08:34:06
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 1499
Non, mon truc a l'air séduisant, mais ne marche pas bien du tout : avec les décalages que je fais de proche en proche pour aller d'un surnuméraire vers un déficit, je me retrouve souvent avec 2 pions alignés sur le même tromino...
#12 - 18-01-2018 19:49:31
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 14
En fait, nodgim place les pépites correctement sur les colonnes et les lignes, et essaye de les déplacer pour recouvrir chaque pièce. Je place les pépites sur chaque pièce, et j'essaie de les déplacer pour que chaque colonne et chaque ligne en contienne le bon nombre.
Ce sont des démarches symétriques, et selon la loi de Murphy, aucune ne va marcher...
Je continue à chercher, mais je me prépare à y passer un certain temps.
#13 - 18-01-2018 23:04:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâtzau 149
Il y a plein de façons d'aborder le problème , j'en ai déjà essayé un paquet :
- Classer les pièces par "type" en fonction de leur orientation et/ou de leur position .
- Générer un graphe en considérant que la pièce en "L" qui occupe la case vide d'un "L" est son successeur .
- Bouger les pépites en partant d'une position d'angle dans chaque "L" .
- Remplir les "L" avec des pépites de 3 couleurs différentes et permuter les couleurs .
- Amorcer une récurrence .
- ...
Tout cela n'a absolument rien donné pour le moment .
Je peux donner les références au problème original si ça intéresse quelqu'un .
Personnellement j'apprends beaucoup de ces problèmes que je traîne comme des boulets pendant des années , je ne trouve rien mais j'apprends plein de choses  
Alors , amusez-vous bien !!!
Vasimolo
#14 - 18-01-2018 23:42:45
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 1149
Je rajoute :
- découper le gâteau en carrés de 3x3, puis mettre 3 pépites sur chaque carré (1 par ligne et 1 par colonne). Ça ne donne rien non plus 
Oui, la référence m'intéresse.
#15 - 19-01-2018 06:17:53
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteu 149
Une autre piste dans l'impasse, pour compléter le tableau :
Je pars des pépites placées dans l'angle des trominos. Je peux toujours les migrer toutes dans les colonnes paires du tableau ( ou lignes ou impaires). Et j'espérais pouvoir montrer que la migration vers les colonnes impaires passait par un équilibre. Chou blanc.
Dans la même veine, le tableau est un vaste damier avec des cases noires et des cases blanches, on peut toujours placer toutes les pépites dans les cases noires, puis on les migre vers les cases blanches en espérant passer par un équilibre ligne / colonne.
Sinon l'option de placer les pépites dans les angles des trominos montre qu'on a beaucoup de marge pour obtenir l'égalité demandée.
#16 - 19-01-2018 11:32:02
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâtteau 149
Ton message #15 me fait remarquer que pour un gâteau rectangulaire de taille 6m*6n, on peut répartir les pièces en 4 ensembles de même cardinal :
* l'ensemble des pièces dont le coin est sur une case de coordonnées (Pair;Pair),
* l'ensemble des pièces dont le coin est sur une case de coordonnées (Pair;Impair),
* l'ensemble des pièces dont le coin est sur une case de coordonnées (Impair;Pair),
* l'ensemble des pièces dont le coin est sur une case de coordonnées (Impair;Impair).
En effet, il y autant de cases de chaque type sur le gâteau, et chaque pièce recouvre 3 cases de 3 types différents, donc crée un déficit de 1 pour le 4e type.
Ca ne servira sans doute à rien mais au cas où...
#17 - 19-01-2018 17:33:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 1449
Voilà où j'ai trouvé le problème : https://artofproblemsolving.com/communi … n_olympiad , il faut aller voir dans "Grade 10 Day 2 Pb 4" . Il y a un lien à droite qui donne quelques propositions de solutions qui sont très loin d'être convaincantes .
Pour la dernière remarque sur la position de la case centrale des pièces c'est évident avec un coloriage du type :
ABCDAB
CDABCD
ABCDAB
CDABCD
ABCDAB
CDABCD
De même pour l'orientation des pièces :
Si A=OO , B = XO , C=OO , D = OX
OX OO XO OO
Alors il y a autant de pièces A que de pièces B et autant de pièces C que de pièces D .
Vasimolo
#18 - 19-01-2018 19:25:18
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 49
De même pour l'orientation des pièces :
Si A=OO , B = XO , C=OO , D = OX
OX OO XO OO
Alors il y a autant de pièces A que de pièces B et autant de pièces C que de pièces D .
Heu, non, là, j'ai un contre-exemple. Il suffit de remplir un carré 9x9, ça fait 27 pièces, et 27 est impair, donc ce n'est pas possible que ce soit équilibré.
#19 - 19-01-2018 19:33:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâteay 149
On est parti sur des côtés multiples de 6 
Vasimolo
#20 - 19-01-2018 20:21:29
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâteay 149
Ben oui, mais si ton carré 9x9 est déséquilibré, tu le reproduis 4 fois, et ça te fait un carré 18x18 déséquilibré.
#21 - 19-01-2018 21:26:21
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 49
Ce n'est pas faux 
Vasimolo
#22 - 30-01-2018 19:12:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
gâreau 149
J'ai pas mal progressé on posant initialement une pépite dans chaque case d'angle puis en déplaçant celle-ci astucieusement pour équilibrer .
Je n'ai rien d'abouti pour le moment mais je suis plutôt confiant ...
Si on trouvait , ce serait un super cadeau pour mon 5000 
Amusez-vous bien !
Vasimolo
#23 - 31-01-2018 08:08:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 1499
J'ai eu la même démarche et j'étais sûr de pouvoir arriver à la solution. C'est en effet tellement facile d'obtenir l'équilibre à partir de toute configuration donnée qu'on se demande bien pourquoi on a tant de mal à prouver que ça marche toujours.....
#24 - 31-01-2018 14:31:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Gâteau 14
C'est la première idée que nous avons tous eu , après il faut trouver une logique pour gérer les déplacements et ce n'est pas facile . J'avais renoncé pour explorer d'autres pistes .
Vasimolo
#25 - 01-02-2018 17:16:31
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
fâteau 149
Aujourd'hui, on s'est étalé là où hier on s'était allé....
A noter :
Si l'on place les pépites aux angles des trominos et qu'on fasse la migration vers le haut ou vers le bas d'un tiers d'entre eux par ligne, on obtiendra une égalité par ligne pour le nombre de pépites, à l'unité près (reste éventuel de la division par 3).
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum