 |
#1 - 09-09-2018 22:53:04
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Badaobum !
Durant cet été, l'office de tourisme du lieu proposait un espace où les estivants pouvaient jouer avec de grands jeux en bois.
Parmi ceux-ci, mon attention a été attirée par un jeu qui comporte un plateau circulaire en bois d'arbre suspendu par un fil à une potence, et sur lequel on vient déposer, un par un et délicatement, des cylindres du même métal. On peut y jouer seul ou à plusieurs, chacun son tour. Après un certain nombre de dépôts, invariablement, les pièces font badaboum, à la plus grande joie des spectateurs.
Je me suis empressé de le reproduire à plus petite échelle :

En ce qui concerne l'exemplaire que vous avez sous les yeux, le plateau a un diamètre Dp = 28 cm, une épaisseur Ep = 1 cm. Il comporte en son centre une vis en acier percée d'un petit trou pour la fixation du fil, et dont la hauteur de tête Ht = 0.6 cm. La masse totale du plateau s'élève à Mp = 350 g.
Les pièces cylindriques, dont le nombre est suffisant pour garantir le badaboum final, ont un diamètre Dc = 2.6 cm, une hauteur Hc = 3.8 cm et une masse mc = 11.5 g. Le coefficient d'adhérence des pièces sur le plateau atteint la valeur assez étonnante f = 0.28.
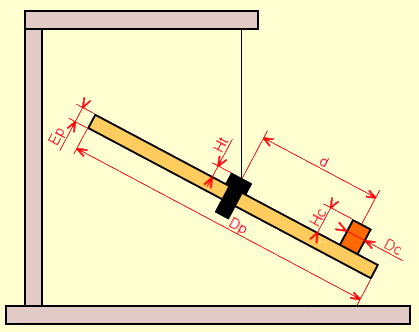
On fera l'hypothèse que toutes ces données sont rigoureusement exactes, que le fil possède une rigidité nulle, qu'il est accroché à la valeur Ht au dessus du plateau, que le centre de gravité du plateau est situé à Ep/2 au dessous de sa surface, que toutes les pièces sont homogènes, que le coefficient d'adhérence est identique sur toute la surface du plateau, que tous les joueurs sont parfaitement intelligents et habiles et que, pendant un jeu, il n'y a ni souffle de vent ni tremblement de terre, et plus encore si affinité.
Pour un jeu en solitaire :
- à quelle distance maximale d du centre du plateau (prise dans la direction de celui-ci) peut-on placer une pièce unique ?
- quel nombre maximum de pièces N peut-on disposer sur le plateau ?
Doit-on respecter une stratégie particulière pour espérer arriver à ce résultat ?
Pour un jeu à deux :
- existe-t-il une stratégie gagnante pour l'un ou l'autre des deux joueurs ? (question ouverte, j'ai bien quelques idées, mais pas de démonstration à proposer...)
(Contrairement à mes habitudes, j'ai adopté le vieux système cgs, mieux adapté aux valeurs utilisées ici, plutôt que le système ISO.)
Spoiler : [Afficher le message] Le calcul du nombre maxi N de pièces s'effectue à partir d'une simple équation sur un axe vertical, le plateau étant supposé horizontal.
Spoiler : [Afficher le message] Ce n'est pas une question de géométrie, c'est une question d'équilibre !
#2 - 10-09-2018 20:12:57
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Badaaboum !
Salut Jackv,
pour le jeu à deux, que dirais-tu de la stratégie suivante : le 2e joueur gagne en jouant systématiquement le symétrique du coup du 1er joueur par rapport au centre du plateau.
Je vais regarder pour le reste.
#3 - 11-09-2018 08:52:28
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
badabpum !
C'est une idée intéressante  . .
J'attends avec intérêt tes réponses aux autres questions.
#4 - 11-09-2018 17:36:59
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Badabom !
Le basculement provient du fait que le centre de gravité "plateau + cylindres" passe au dessus du centre de poussée (accrochage du plateau au fil) au delà d'un certain nombre de cylindres posés. Le moindre déséquilibre (1 cylindre supplémentaire) dans cette condition d'équilibre instable fait basculer le plateau.
Je ne suis pas certain que, une fois qu'on a dépassé le nombre de cylindres qui fait passer le centre de gravité au dessus du centre de poussée, il y ait vraiment une stratégie pour placer 1 cylindre de plus, car dans ce cas tout déséquilibre est fatal. On pourra toutefois tenter de remplir le plateau de l'extérieur vers l'intérieur.
J'ai bien aimé le "bois d'arbre" et le cylindre du "même métal" .
#5 - 11-09-2018 18:38:42
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Badabboum !
Toutes tes remarques sont parfaitement judicieuses. Je n'en attendais pas moins  . .
Il ne te reste plus qu'à donner des valeurs chiffrées  . .
J'ai bien aimé le "bois d'arbre" et le cylindre du "même métal" .
  ! Merci. ! Merci.
#6 - 11-09-2018 22:48:51
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Badaboum
Je tente ma chance pour la toute première question. Vu mon peu d'expérience dans ce domaine il risque d'y avoir quelques erreurs, qui, je n'en doute pas, n'échapperont pas à ton regard perçant 
Je me place dans un repère centré à l'endroit de la fixation du fil sur la vis. L'axe des x est horizontal dirigé vers la droite, et l'axe des y vertical dirigé vers le haut.
Je nomme a l'angle entre le plateau et l'horizontale, à savoir, a=0 si le plateau est parfaitement horizontal.
Le centre de gravité du plateau a pour coordonnées : (-(Ht+Ep/2)sin(a) ; -(Ht+Ep/2)cos(a)).
Le centre de gravité du cylindre a pour coordonnées : (d.cos(a)+(-Ht+Hc/2)sin(a) ; -d.sin(a)+(-Ht+Hc/2)cos(a)).
Si l'ensemble est à l'équilibre, alors le centre de gravité de l'ensemble est à la verticale du fil, donc son abscisse est nulle :
-(Ht+Ep/2)sin(a).Mp+(d.cos(a)+(-Ht+Hc/2)sin(a)).Mc = 0
d'où d = [(Ht-Hc/2)+(Mp/Mc).(Ht+Ep/2)]tan(a).
Enfin, si le cylindre est à la limite de glisser, on a tan(a)=f.
Application numérique : d vaut environ 9,01 cm.
#7 - 12-09-2018 11:48:08
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Baadaboum !
L'angle maximal pris par le plateau est limité soit par le renversement de la pièce cylindrique, soit par le glissement de celle-ci.
Renversement: il faut que: tg(A) < Dc/Hc, soit tg(A) < 0,68
Glissement: force le favorisant = mg.sin(A) et force le combattant = f.mg.cos(A)
il faut donc finalement: tg(A) < f, soit tg(A) < 0,28
C'est donc le glissement de la pièce cylindrique qui dimensionne l'angle maximal.
Je reviendrai pour la suite. Affaire à suivre ....
#8 - 12-09-2018 18:22:22
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Badabum !
Félicitations à Ebichu  . .
Je suis OK avec le calcul de la distance d.
Mais mon idée première, c'était surtout de calculer le nombre de pièces maxi qu'on pouvait disposer sur le plateau et de savoir comment il fallait s'y prendre, ce que tu as déjà dit nodgim as déjà compris.
Franky : c'est un début ; comme tu le dis "A suivre" 
#9 - 12-09-2018 19:43:40
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Badaboum !!
Je ne comprends pas, qu'est-ce que j'ai dit ?
Pour le reste, à savoir le nombre maximal de pièces qu'il est possible de disposer quand on joue tout seul, je doute qu'il existe une réponse simple.
Pour simplifier le problème, on peut enlever une dimension au plateau (plus exactement, passer de la dimension 2 à la dimension 1), et imaginer un plateau rectangulaire, sur lequel on place des cylindres obligatoirement sur la ligne médiane du rectangle (j'espère bien me faire comprendre).
Même dans ce cas simplifié, la réponse n'est pas évidente. À la stratégie triviale consistant à : "placer un cylindre à gauche du centre, le plus près possible du centre, puis à droite le plus près possible du centre, puis continuer en alternant gauche et droite", on peut opposer une stratégie plus subtile :
* on place le premier cylindre le plus près possible du centre, à gauche
* puis le deuxième cylindre, à droite, mais éloigné de Dc/2 du centre du plateau
* puis on alterne gauche/droite et plaçant les cylindres les plus près possible du centre à chaque fois.
Cette deuxième stratégie limite le déséquilibre et devrait donc permettre d'aller plus loin.
#10 - 12-09-2018 22:08:52
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
badaboym !
Ebichu a écrit:Jackv a écrit:ce que tu as déjà dit.
Je ne comprends pas, qu'est-ce que j'ai dit ?
Au temps pour moi, je suis confus de ma confusion  . .
C'est Nodgim qui avait trouvé la bonne méthode... (le message a été corrigé)
Inutile de chercher à simplifier le problème, le nombre maxi de cylindres n'est pas trop difficile à calculer, la formule est même un peu plus simple que celle que tu as utilisée pour trouver la distance maxi.
Quant aux stratégies que tu imagines pour placer le maximum de pièces sur le plateau, elles courent droit à l'échec  . .
#11 - 12-09-2018 23:47:46
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
badzboum !
Salut 
"Toutes hypothèses faites" et avec les données fournies on a au plus simple :
Pour la distance d
[TeX]d=[(H_t+\frac{E_p}{2})\cdot \frac{M_p}{M_c}+H_t-H_c]\cdot f\approx 8.48 \,\mathrm{cm}[/TeX]
Pour le nombre N
...
#12 - 13-09-2018 09:45:17
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
#13 - 13-09-2018 19:07:41
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Badabou !
Pour cette question, je ne vois pas trop, je vais courageusement attendre que la réponse de nodgim se dévoile 
#14 - 13-09-2018 23:03:00
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Badabouum !
Effectivement, j'avais mis le demi au frais ...
[TeX]d=[(H_t+\frac{E_p}{2})\cdot \frac{M_p}{M_c}+H_t-\frac{H_c}{2}]\cdot f\approx 9.01 \,\mathrm{cm}[/TeX]
Pour le reste je reviendrai 
#15 - 13-09-2018 23:40:52
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
#16 - 14-09-2018 19:36:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Badaboum
Je trouve que ça bascule au 26 ème cylindre.
Pas eu besoin de me servir des poids, juste les dimensions ont suffi.
#17 - 14-09-2018 23:11:40
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Badaboum !!
EDIT :
nodgim : Je ne trouve pas tout à fait OK pour la même valeur numérique du nombre de pièces ...
Mais Ton hypothèse de calcul me semble un peu trop simplifiée.
J'ai ajouté un indice.
#18 - 15-09-2018 00:52:27
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Badabouum !
Autre proposition en se basant sur un pavage du disque de rayon [latex]d[/latex] avec des triangles équilatéraux de coté [latex]D_c[/latex] :
[TeX]N=6\cdot (2^{\lfloor\frac{d}{D_c}\rfloor}-1)=42[/TeX]
Edit : pas sur de bien saisir l'indice ... faut-il comprendre que l'on peut empiler les pièces ?
#19 - 15-09-2018 07:43:32
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Badabouum !
Non Sydre, ce n'est pas une histoire de pavage et se serait contre productif d'empiler des pièces.
Mais cela se passe bien à la verticale  . .
#20 - 15-09-2018 19:01:03
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
badanoum !
J'ai ajouté un deuxième indice  . .
#21 - 17-09-2018 00:23:35
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Badabum !
Merci à tous les participants  . .
Félicitations particulières à Ebichu, le premier à avoir répondu à la première question et dont je vous invite à suivre la démonstration post 6, et à nodgim, le seul à avoir répondu à la deuxième, même si sa réponse, un peu laconique mérite un petit complément :
Pour avoir un équilibre stable, la position du centre de gravité "plateau + cylindres" doit rester en dessous du point d'attache du plateau.
d'où N * Mp * (Hc/2 - Ht) < Mc * (Ep/2 + Ht)
N < (Mc / Mp) * (Ep/2 + Ht) / (Hc/2 - Ht) soit N < 25,75
N = 25
A la lumière de ce résultat, je vous laisse encore réfléchir aux meilleures stratégies pour le jeu en solo ou le jeu à deux,
#22 - 17-09-2018 08:14:39
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
badanoum !
Je ne comprends pas le lien entre la phrase en italique et la formule, ni entre la formule et 25,75. Tu es sûr que tu n'as pas fait une erreur en la recopiant ?
#23 - 17-09-2018 09:40:37
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Badaobum !
Je me suis en effet complètement mélangé les pinceaux dans les indices de variable  ... ...
Merci, Ebichu, de me l'avoir signalé  . .
C'est corrigé, correctement j'espère.
#24 - 17-09-2018 14:55:48
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Badabomu !
Non, toujours pas  Tu as inversé Mc et Mp. Tu as inversé Mc et Mp.
#25 - 17-09-2018 15:38:19
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Baadboum !
Oui, effectivement, il y a un truc pas au point dans l'équation posée.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








