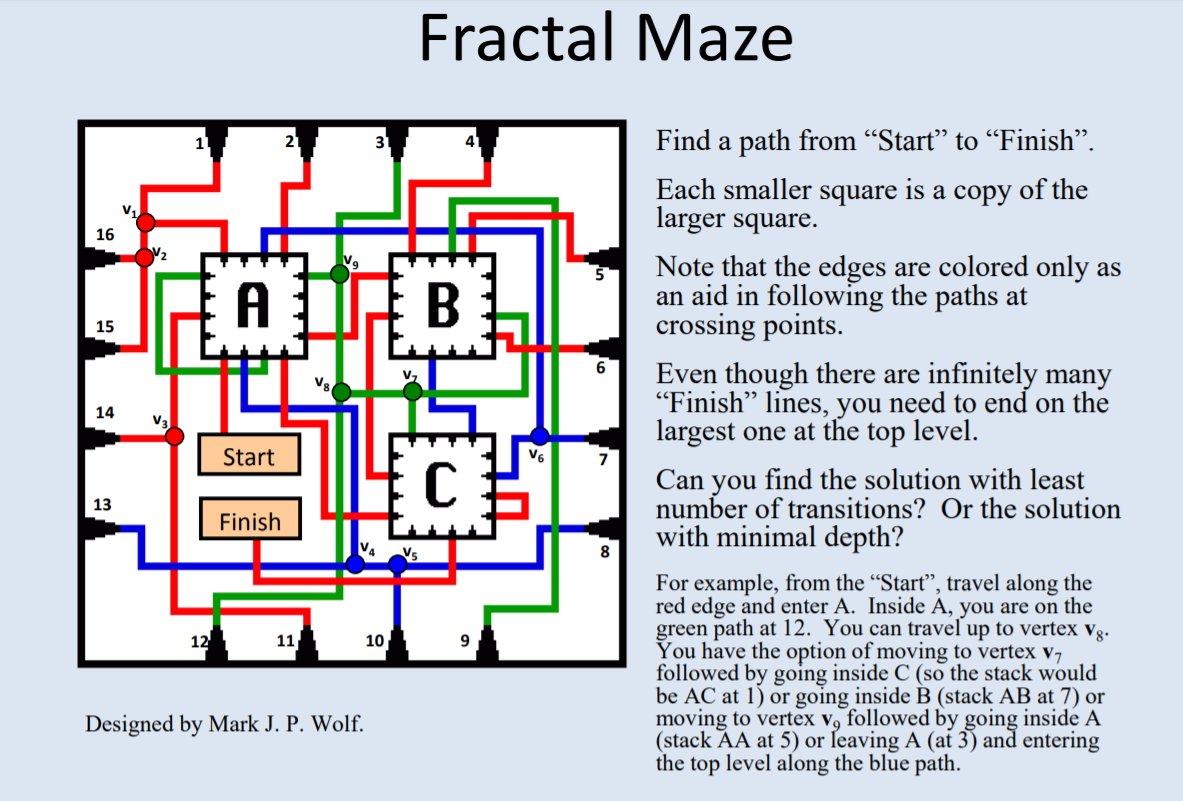
Merci à tous les participants!

Mes résultats:

Sur la profondeur:
On peut déjà montrer facilement qu'elle est bornée par le nombre E (entrées externes), ça se fait en procédant itérativement: on regarde le labyrinthe en se demandant quelles entrées sont liées ensemble en autorisant une profondeur "N", et on injecte ce composant dans lui même (on rajoute une couche de profondeur à l’extérieur), ce qui nous permet de déduire la nouvelle partition des entrées, représentant qui est relié à qui en autorisant N+1 niveaux. Lors de cet itération, on ne peut que "fusionner" des listes d’entrées qui étaient reliées ensemble en autorisant N niveau pour construire les listes d'entrées qui sont maintenant reliées ensemble en autorisant N+1 niveau. Donc au pire on démarre d'une partition ou chaque entrée serait seule (liée à personne en autorisant 0 récursion) et on voit bien qu'en opérant des fusions entre les ensembles de ces partitions on n'en fera qu'au max E (ou alors on aura 2 étapes qui ne changent pas la partition des entrées liées ensemble et du coup ça veut dire qu'elles ne le seront jamais qq soit le nombre d’itération, c'est stable).
Un bon candidat de labyrinthe pour maximiser cela s'obtient en généralisant la partie gauche du petit labyrinthe gris de d'entrainement de l'autre thread (la flemme de dessiner)

Sur la longueur:
Cette construction itérative est déjà très intéressante:

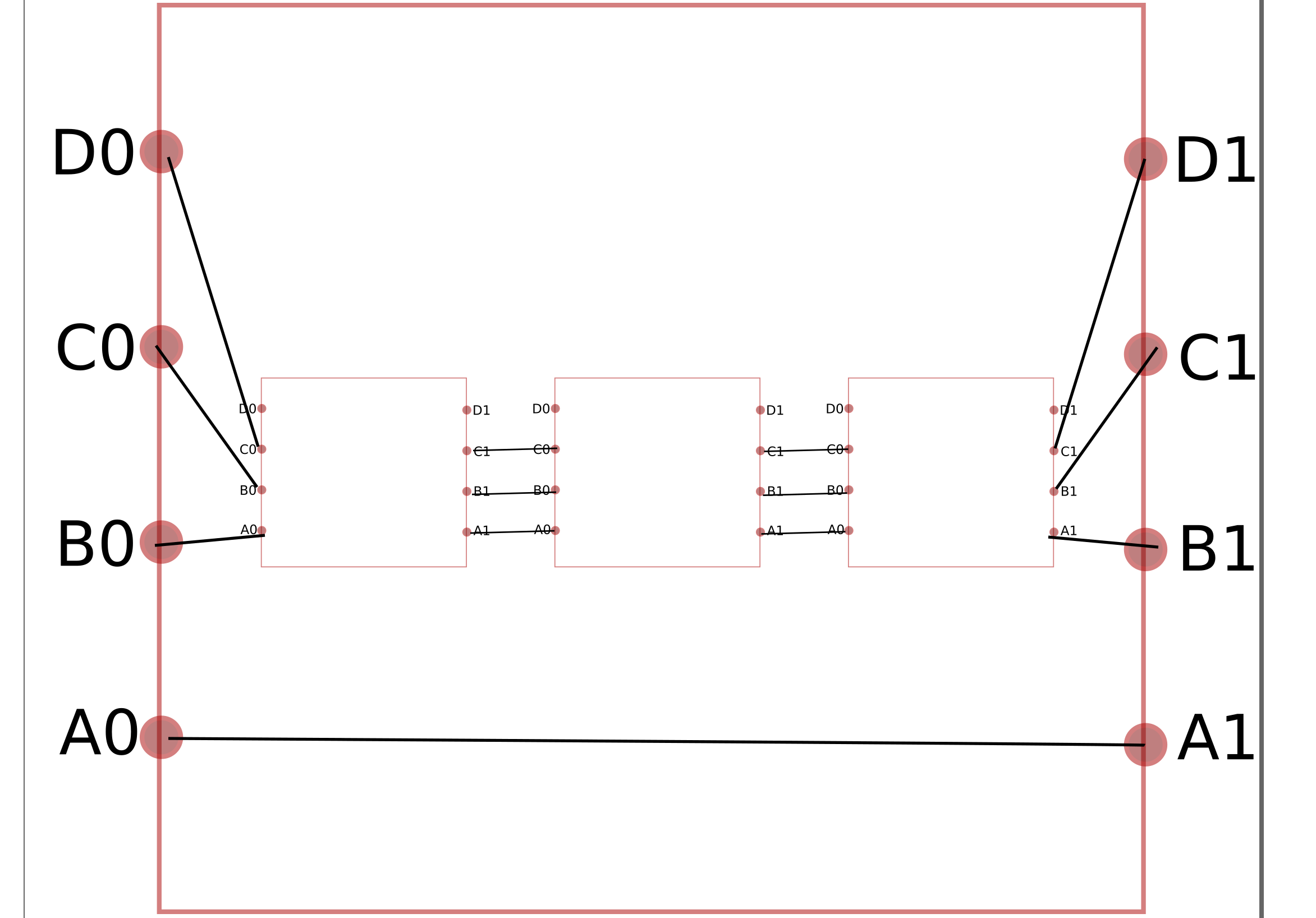
Et ça peut continuer autant qu'on veut et quelque soit le nombre C, il suffit de rajouter des paires d’entrées pour avoir l’itération suivante.
Si C est le nombre de copies du labyrinthe dans lui même, on voit qu'entre une itération et la suivante (un ajout de paire d’entrées selon ce motif de construction) on multiplie le trajet par C et on ajoute C+1 segments.
C'est a dire que pour un labyrinthe avec 12 entrées externes et 4 copies internes, cette construction assure qu'une certaine paire de ses entrées sera liée par un chemin de longueur minimale 2729!

Mais je sais aussi que ce n'est pas le max car certaines constructions sont plus efficaces, par exemple:

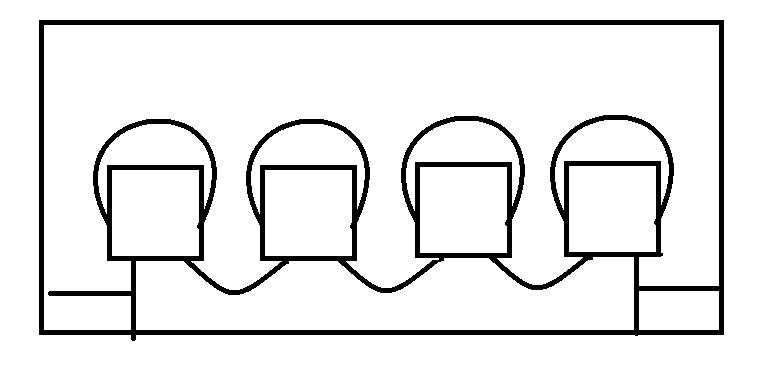
Ici on a que E=4 et C=4 et pourtant la distance entre 2 entrées éloignées est de longueur 17! (alors que la construction précédente donnerait seulement 9)

Mais cette construction ne se généralise pas facilement. En fait on se rend compte souvent que la "dernière itération" (dans une construction incrémentale) peut souvent être optimisée mais que c'est au détriment de pouvoir continuer la construction itérative (si on continue cette optimisation fournit un "raccourci" pour les itérations suivante et donc met fin à une construction exponentielle efficace).