Hello!

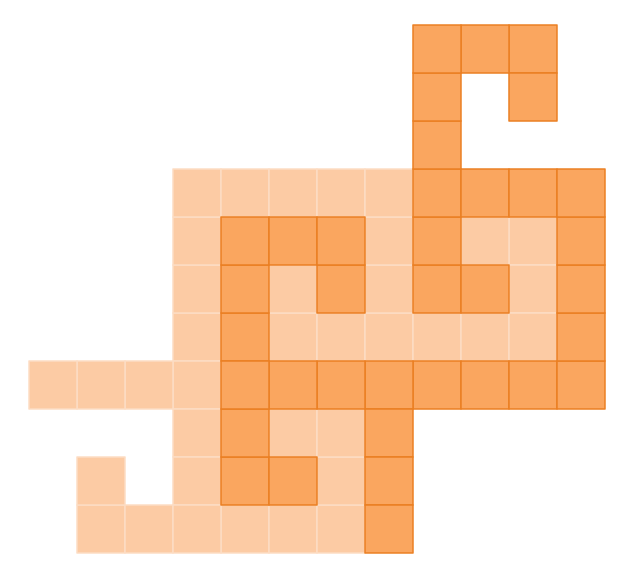
Une catégorie d’énigmes qui m'a toujours fasciné c'est le decoupage de forme en 2 parties "identiques". Et j'ai toujours voulu ajouter ma petite creation perso à cette famille, c'est maintenant chose faite, la voici:


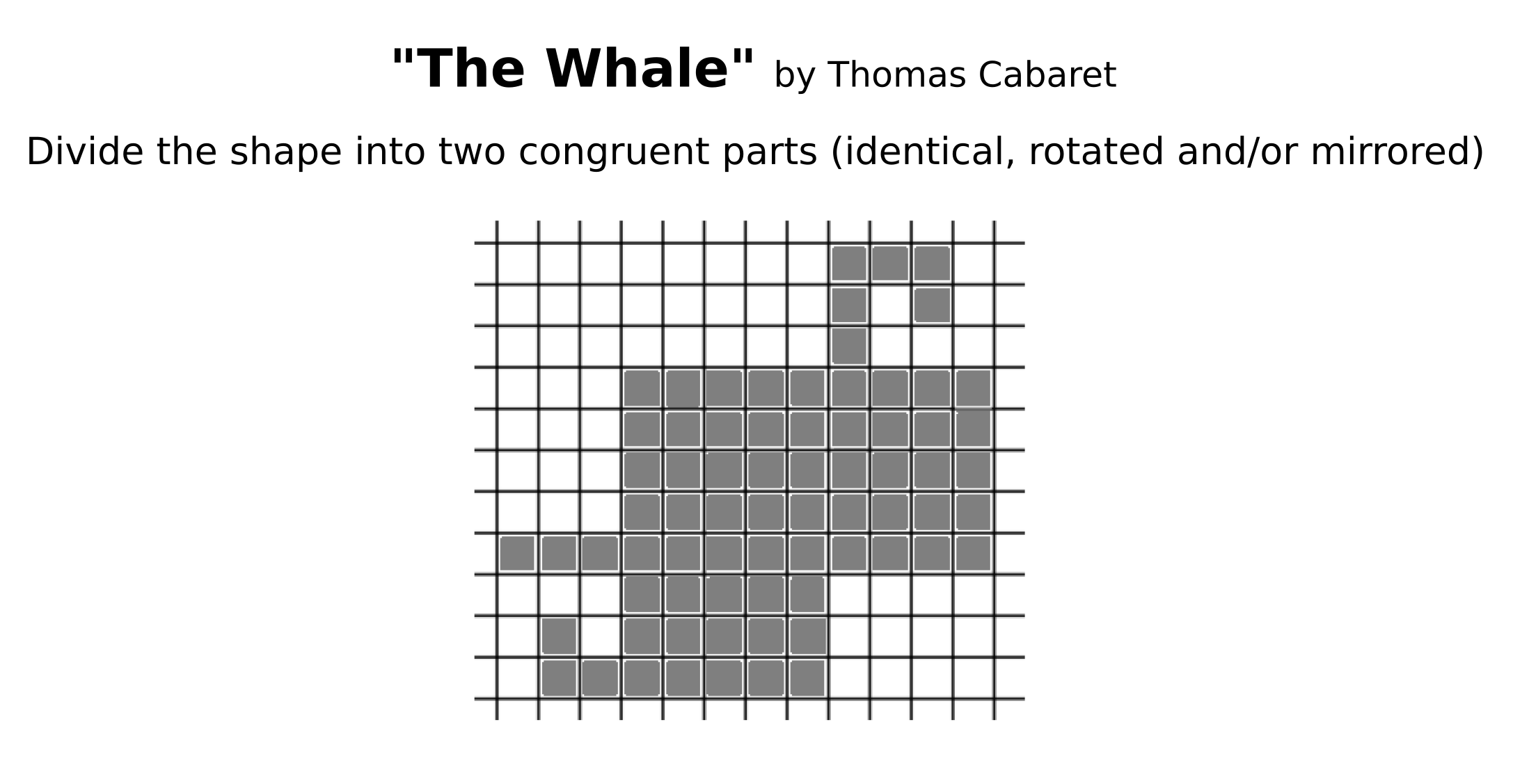
(L'imagine est zoomable)

L'objectif est donc de découper la forme en 2 parties superposables (identiques à une translation, rotation et/ou symétrie miroir prés d'une moitié à l'autre), et je précise que ca se fait avec une seule coupe continue (car en ne le précisant pas certains sont venus me proposer des solutions avec des pieces non connexes...)

Mettez vos réponses dans un bloc spoiler si possible.

Et je l'ajoute en anglais, histoire que les moteurs de recherche le trouve:
Divide the shape into two congruent parts (identical, translated, rotated and/or mirrored) by a single and continuous cut.

Bonne chance!

Réponse et éléments de réponse:

Tips1:
Spoiler : [Afficher le message]
Remarque sur le périmètre:
Appelons "pôles" les 2 extrémités de la ligne de coupe (2 points sur le périmètre de la forme initiale donc) Les poles séparent le périmètre extérieur en 2 demi périmètres d’égale longueur (c'est trivial car comme les 2 moitiés sont la meme piece et ont la frontière de coupe en commun, le reste doit être égale)
On remarque qu'on peut trouver une formulation plus forte de cette regle en ne considérant pas juste la longueur mais l'ensemble des longueurs de segments: dans la majorité des cas les ensembles de segments de part et d'autre des poles sur le périmètre extérieur doivent être les memes, par exemple s'il ya une longueur 5, une longueur 2, et une longueur 3 de segment sur un demi périmètre on doit retrouver 5,2,3 sur l'autre. MAIS il y a des cas subtiles ou ce n'est pas exactement cela et ou un des segment se split en deux (par exemple un 5 qui devient une paire 1-4 sur l'autre demi périmètre), ca se produit lorsque la coupe à un des poles est en prolongement d'un segment extérieur.
Quelque soit la regle qu'on utilise on peut fortement restreindre la position des poles grace à cette heuristique. Et on peut aussi commencer par colorier en 2 couleurs toutes les cellules des demis périmètres qui sont donc sur des moitiés distinctes.

Tips2:
Spoiler : [Afficher le message]
Technique de l'appariement
Sur une autre figure:

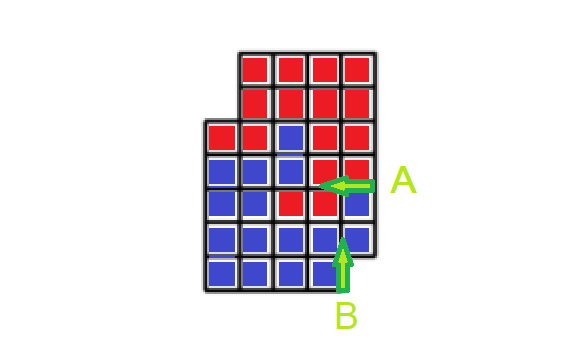
Pour un candidat de pôles envisageables, on peut trouver plus facilement un profil de coupe avec la technique de l'appariement. Ci dessus on peut reporter en A le trajet fait depuis B. Lorsqu'on définit ainsi des points et des directions d'appariement ca ne donne qu'un candidat de coupe possible (et du coup soit ca marche soit on se rend compte vite que ca ne marche pas)
On remarque que sur cette figure la regle des ensembles de longueurs sur les 2 demi périmètre s'applique, coté rouge on a 1,1,2,4,4 et coté bleu on a 2,1,1,4,4, ce qui est le meme ensemble.

SOLUTION: voir les propositions ci dessous.
Spoiler : [Afficher le message]
On remarque que sur ma figure la regle des ensembles de longueurs sur les 2 demi périmètres est dans le cas particulier dont je parle, d'un cote on a:
6,2,1,1,1,2,3,1,3,4,5
et de l'autre:
3,3,2,1,1,1,2,3,5,4,3,1
Sur le second le 6 du premier devient 3,3 mais à cette exception pres c'est le meme ensemble.