 |
#1 - 28-12-2009 22:29:04
- nurarihyon
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 9
roblème geometrique
bonjour à tous, je poste ici car j'ai affaire à un problème assez coriace et je n'ai aucune idée de comment le résoudre:
ABC est un triangle équilatéral.M et N sont deux points quelconques situés à l'intérieur de ce triangle. les droites ( MM1 ) (MM2) (MM3) (NN1) (NN2) (NN3)
sont respectivement perpendiculaires aux cotés du triangle ABC comme l'indique la fig ci dessous.
démontrer que MM1+MM2+MM3=NN1+NN2+NN3.
j'ai l'impression que la somme des 3 droites perpendiculaires qui se coupent en un meme point dans le triangle est égale à une hauteur et que du coup l'égalité est verifiée mais je suis pas sur.
merci à toutes les réponses/indices que vous pourrez me fournir.
#2 - 28-12-2009 22:47:40
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Probllème geometrique
Ca aiderai peut-etre si tu fournissais la figure en question.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#3 - 28-12-2009 22:49:01
- nurarihyon
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 9
#4 - 28-12-2009 22:52:56
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
provlème geometrique
As-tu calculé les aires des triangles AMB, BMC et CMA ? Et leur somme ?
Est-ce ce dessin pour M ?
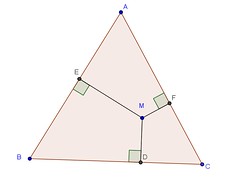
Celui qui fuit les casse-tête ne vaut pas un clou.
#5 - 28-12-2009 23:48:23
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Prooblème geometrique
nurarihyon a écrit:et comment on fait?
On commence par faire un beau dessin, pas trop petit, et pas trop grand, on le sauve au format PNG (qui contrairement au format JPG ne pert pas d'information).
Puis on le télécharge ICI ou sur n'importe quel autre site qui conserve des images, comme imageshack, flicker...
Mais attention aux imitations, certains sites ont des noms similaires, mais ne font que collectionner les addresses email pour envoyer du spam.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#6 - 29-12-2009 09:09:59
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
problème heometrique
Moi, j'obtiens que le triangle doit être équilatéral.
AB*MM1 + AC*MM2 + BC*MM
= ABC
= AB*NN1 + AC*NN2 + BC*NN3
--> AB * (MM1-NN1) + AC * (MM2-NN2) + BC * (MM3-NN3) = 0
Il faut que AB=AC=BC pour que MM1+MM2+MM3 = NN1+NN2+NN3.
Contre-exemple si le triangle n'est pas équilatéral:
Soit AB=AC >> BC, prenons M tendant vers A et N tendant vers B.
MM1+MM2+MM3 tend vers une valeur supérieure à AB
tandis que NN1+NN2+NN3 tend vers une valeur inférieure à BC, donc inférieure à AB.
Bref, l'hypothèse est vérifiée si et seulement si le triangle est équilatéral.
#7 - 29-12-2009 10:20:00
- falcon
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 106
Prolbème geometrique
Tu devrais relire l'énoncé. C'est précisé que le triangle est équilaterral.
Il faut aussi faire attention aux érreurs de logique :
tu donnes un contre exemple dans le cas ou le triangle n'est pas éqilateral. Tu as juste montré qu'un certain triangle qui n'est pas équilatéral ne vérifie pas la propriété demandée pour un certain point M et N. En aucun cas tu n'as montré que " l'hypothese est vérifiée si et seulement si le triangle est équilateral"
Sinon, ton intuition est bonne nurahyon et je te conseil de suivre le conseil de scrablor
Il vaut mieux pomper meme s'il ne se passe rien que risquer qu'il se passe quelque chose de pire en ne pompant pas
#8 - 29-12-2009 10:56:49
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
Problèm geometrique
Ah oui en effet. C'était mis dans l'énoncé. 
Par contre, je ne vois pas d'erreur de logique. En démontrant que le triangle doit être équilatérale pour que MM1+MM2+MM3=NN1+NN2+NN3, j'ai aussi démontré que cette égalité était vérifiée si le triangle est équilatéral.
Le contre-exemple, n'est là que pour illustrer. De plus, il s'agit d'un triangle isocèle quelconque. Le but étant de s'éloigner du triangle équilatérale. Aucune précision étant faite quant à ses dimensions, les conclusions sont valables pour tous les triangles isocèles. Pour un triangles quelconque, c-à-d toujours plus éloigné du triangle équilatéral, les conclusions sont toujours vrai puisque je ne me réfère pas aux propriétés d'un triangle isocèle dans mon contre-exemple. Et ce pour tous les triangles quelconques. Bref, il s'agissait peut-être d'un contre exemple, mais il illustre tous les triangles non-équilatéraux.
Je pense que tu as parlé d'erreur de logique un peu vite.
#9 - 29-12-2009 10:57:52
- nurarihyon
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 9
Probllème geometrique
le problème c'est qu'on nous donne aucune longueur, il faut juste déduire que MM1+MM2+MM3=NN1+NN2+NN3.
et je n'ai trouvé aucune proprièté qui confirme ce que je pense...
#10 - 29-12-2009 11:01:39
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
problème geomerrique
Miam miam. Je mange ma main...
#11 - 29-12-2009 11:04:54
- nurarihyon
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 9
problème geomrtrique
sinon la figure est correcte, il faut juste mettre N de la meme manière que M aléatoirement dans le triangle.
mais comment t'en déduis que AB*MM1+AC*MM2+BC*MM3=ABC?
en tout cas merci à tous, je suis plus avancé qu'avant.
#12 - 29-12-2009 11:16:41
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
Problème geometriqu
A partir de M, tu définis 3 triangles dont la somme des airs vaut l'air du triangle.
AB*MM1 = air du triangle ABM
AC*MM2 = air du triangle ACM
BC*MM3 = air du triangle BSM
AB*H = air du triangle ABC
Il vient,
AB*MM1 + AC*MM2+BC*MM3 = AB*H
mais comme AB = AC = BC, après simplification par AB, tu trouves finalement,
MM1+MM2+MM3 = H = constant
et ce quelques soit la position du point M à l'intérieur ou sur le périmètre du triangle ABC.
#13 - 29-12-2009 11:21:00
- falcon
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 106
problème geomztrique
l'assertion : "l'hypothese est vérifié implique le triangle est équilaterral" est fausse
pour justifier cela, un exemple ou l'hypothese est vérifiée et le triangle n'est pas équilatéral.
Par exemple un triangle ABC isocel en Aet non équilaterral, et H le projeté orthogonal de A sur BC. un point M à l'intérieurde ABC et N son image par la symétrie d'axe AH.
L'égalité est vérifié. C'est immédiat par symétrie. Pourtant letriangle n'est pas équilaterral.
donc quand tu as dit "l'hypothese est vérifié si et seulement si le triangle est équilaterral", il aurait fallu nuancer
la vérité est que "l'hypothese est vérifié pour tout points M et N à l'intérieuredu triangle si et seulement si le triangle est équilaterral"
Montrons cela:
premier sens : suppossons que l'hypothese est vérifiée pour tout points M et N.
Montrons qu'alors le triangle est équilaterral.
elle est en particulier vérifiée pour M = A et N = B on en déduit que le hauteur issue de A est égale àcelle issue de B, en prenant ensuite M=A et N = C on en déduit que les trois hauteurs sont égales. En notant h cette hauteur et en calculant l'aire du triangle on obtient AB x h = AC x h = BC x h
le triangle est donc bien équilateral.
Deuxieme sens Suposons que le triangle est équilaterral et mopntrons que l'hypothese est vérifiée:
Soit M et N quelquoncs à l'intérieur du triangle.
AB*MM1 + AC*MM2 + BC*MM = AB*NN1 + AC*NN2 + BC*NN3
--> AB * (MM1-NN1) + AC * (MM2-NN2) + BC * (MM3-NN3) = 0
Comme ABC est équilateral AB=AC=BC
Ainsi MM1+MM2+MM3 = NN1+NN2+NN3.
cqfd
Amicalement
Il vaut mieux pomper meme s'il ne se passe rien que risquer qu'il se passe quelque chose de pire en ne pompant pas
#14 - 29-12-2009 11:22:02
- nurarihyon
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 9
Poblème geometrique
cette fois ci j'ai vraiment compris! merci pour tout, je m'étais inscrit juste pour avoir ma réponse alors c'est vous dire si j'ai bloqué.
#15 - 29-12-2009 11:27:19
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Problème geeometrique
Maintenant que tu es inscrit tu peux essayer les énigmes ;-)
http://enigmusique.blogspot.com/
#16 - 29-12-2009 12:21:22
- nurarihyon
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 9
#17 - 29-12-2009 12:26:41
#18 - 29-12-2009 12:29:02
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Problèm egeometrique
nurarihyon a écrit:je ferai de mon mieux!
Commence par cliquer sur jouer, c'est l'énigme 1 qui est là pour expliquer comment ça marche ;-)
http://enigmusique.blogspot.com/
#19 - 29-12-2009 13:26:52
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
Probllème geometrique
falcon a écrit:l'assertion : "l'hypothese est vérifié implique le triangle est équilaterral" est fausse
J'ai pas dit ça.
falcon a écrit:pour justifier cela, un exemple où l'hypothèse est vérifiée et le triangle n'est pas équilatéral.
Tu devrais trouver un triangle particulier où M et N quelconques vérifient l'hypothèse. Si tu prends M et N particuliers, tu ne vérifies pas l'énoncé.
falcon a écrit:Par exemple un triangle ABC isocèle en A et non équilatéral, et H le projeté orthogonal de A sur BC. un point M à l'intérieur de ABC et N son image par la symétrie d'axe AH.
L'égalité est vérifié. C'est immédiat par symétrie. Pourtant le triangle n'est pas équilatéral.
Tu prends deux points particuliers pour démontrer que je ne peux pas démontrer que l'hypothèse est vérifiée.
Moi, je prends deux points particuliers pour démontrer que l'hypothèse n'est pas vérifiée dans le cas d'un triangle non-équilatéral.
Je démontre par l'absurde que le triangle doit être équilatéral.
falcon a écrit:donc quand tu as dit "l'hypothèse est vérifié si et seulement si le triangle est équilatéral", il aurait fallu nuancer
la vérité est que "l'hypothèse est vérifié pour tout points M et N à l'intérieure du triangle si et seulement si le triangle est équilatéral"
M et N sont quelconques. C'est mis dans l'énoncé.
Les deux phrases sont donc équivalentes.
Quoiqu'il en soit, j'ai mal lu l'énoncer puisque le triangle est équilatéral par hypothèse. C'est une erreur de distraction, pas une erreur de logique.
#20 - 29-12-2009 13:35:31
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Problème geometrque
C'est une erreur de distraction
c'est la plus fréquente, j'en fais beaucoup et quand je fais des maths avec ma fille, c'est ce que je lui reproche le plus 
http://enigmusique.blogspot.com/
#21 - 29-12-2009 13:45:40
- falcon
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 106
problème geoletrique
Ok milou !
juste une histoire de quantificateurs implictes donc ^^
Il vaut mieux pomper meme s'il ne se passe rien que risquer qu'il se passe quelque chose de pire en ne pompant pas
#22 - 29-12-2009 14:45:20
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
probkème geometrique
Milou_le_viking a écrit:Miam miam. Je mange ma main...

Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#23 - 29-12-2009 14:47:23
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Problème geoemtrique
C'est du régional, ou quoi ?
http://enigmusique.blogspot.com/
#24 - 29-12-2009 14:50:42
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
problème feometrique
En Sologne on cuisine la tarte tatin ; en Pologne, où les gens sont plus "selfish", on se cuisine une "marme ma main" 
(Je suis déjà dehors.)
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







