 |
#1 - 15-03-2011 23:05:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 15-03-2011 23:13:21
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
zchecs 9
Je suis tenté de dire que cette façon de retourner les jetons donera a la fin de chaque étape un nombre de jetons de chaque couleur pair.
Une éventuelle preuve a cela s'appuierait sur le fait qu'un mouvement va, soit annuler le mouvement précédent (le cas le plus trivial), soit retourner tous les jetons d'une ligne ou d'une colonne du mouvement précédent, soit retourner exactement deux jetons touché par le mouvement précédent. Dans chacun des cas, et vu que les dimensions de la grille sont paires, le nombre de jetons dont la face rouge (respectivement blanche) est en haut est pair.
J'en conclurais que ta figure est impossible a réaliser car elle compte un nombre de faces rouges (ou blanches, c'est pareil) impair.
A formaliser... en espérant que mon intuition est bonne.
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#3 - 16-03-2011 03:24:35
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Ehecs 9
Il faudrait retourner 19 pions en tout pour y arriver.
Or j'ai un invariant dans ce problème : le nombre de pions rouges (ou blancs) du plateau est paire. En effet, a chaque retournement d'une ligne ou d'une colonne, je ne peux pas ajouter ou enlever un nombre impair de jetons rouges. Si j'avais x jetons rouges sur une ligne, j'en aurai 8-x après avoir retourné la ligne (ou la colonne). Je oeux donc soit perdre 8, 6, 4, ou 2 jetons, en gagner 8, 6, 4, ou 2 jetons, ou en avoir toujours le même nombre. Dans tous les cas, la parité du nombre de rouges ne change pas.
Comme il y a un nombre paire de rouges au début, en l'occurrence 0, il en est de même a tout moment.
Il est donc impossible d'arriver a la configuration ci dessus qui compterait 19 pions rouges :-)
Dommage !
#4 - 16-03-2011 09:28:07
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Echesc 9
non !
Pour s'en convaincre, prenons au hasard 4 cases formant un rectangle parallèle aux bord de l'échiquier.
Ces cases sont "animées" par 4 opérations possibles (2 lignes et 2 colonnes) qui ont pour effet de transformer 2B en 2R, 2R en 2B ou RB en BR en laissant intact l'autre rangée. Si l'on part de 4 blancs, on aura toujours un nombre pair de Blancs (et de Rouge) sur nos 4 cases.
Ce n'est pas le cas sur la figure fil (il y a plein de rectangles de 4 cases formés de 3 R et 1 B ou l'inverse), elle n'est donc pas le résultat d'une suite de retournement de lignes et de colonnes.
#5 - 16-03-2011 11:54:43
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
EEchecs 9
Encore une fois, il faut trouver l'invariant.
Ici, on a : "Le nombre de cases blanches est pair, et le nombre de cases rouges aussi".
> C'est bien le cas au début
> Sur chaque ligne ou colonne que je retourne, il y a un nombre B de blancs au départ, et 8-B rouges du coup. Après retournement, j'obtient 8-B blancs et B rouges. Le nombre Nb de blancs total passe alors à Nb -B + 8-B = Nb + 8-2b, dont la parité ne change pas. Pareil pour les rouges.
Ce n'est pas le cas à la fin (19 rouges), donc pas la peine d'essayer...
#6 - 16-03-2011 13:30:38
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#7 - 16-03-2011 16:36:34
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Ececs 9
Mon coup de "exactement deux jetons" va dans ce sens. Peux-tu néanmoins me dire si mon explication te paraît compréhensible, et dans ce cas, si elle te paraît juste ? Merci 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#8 - 16-03-2011 17:17:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
ecjecs 9
Non Mathias , ton raisonnement ne tient pas 
Chaque fois que tu choisis une case tu retounes 15=8+8-1 pions donc la parité du nombre de pions de chaque couleur change .
Vasimolo
#9 - 16-03-2011 17:57:48
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
evhecs 9
La réponse est "Oui c'est possible". Voici les retournements à effectuer
Ligne 1: 1, 3, 4, 5
Ligne 2: 3, 7, 8
Ligne 3: 1, 4, 5, 6
Ligne 4: 1, 2, 5, 6
Ligne 5: 3, 7, 8
Ligne 6: 1, 3, 4
Ligne 7: 2, 5
Ligne 8: 2, 5
"Simple" système de 64 équations booléennes à 64 inconnues
#10 - 16-03-2011 19:00:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Echecs
Oui Scarta et il y a une explication réellement très simple 
Vasimolo
#11 - 16-03-2011 19:30:14
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1971
Echhecs 9
En effet : je considère le pion (a,b), les 15 opérations de retournement sur les pions (a,i) et (j, b) nous donne le même tableau qu'au départ avec pour seul pion retourné le pion (a,b).
Il est donc possible de retourner n'importe quel pion sans modifier les autres, et du coup de réaliser cette figure (ou n'importe quelle autre d'ailleurs)
#12 - 16-03-2011 19:51:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
checs 9

Vasimolo
#13 - 16-03-2011 21:38:39
- Bamby2
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 152
ecjecs 9
hummm, si on retourne une ligne ou une colonne, on retourne 8 cases, donc le nombre restera toujours paire, ce n'est donc pas possible.
si on retourne le deux, alors en "activant" les 15 cases de la lignes et la colonne de se point, tous les points de l'échiquier sont touché un nombre paire de fois (8 fois sur la lignes/colonne, et 2 fois les autres) sauf le points central qui est touché 15 fois.
en gros on ne retourne que 1 point, celui voulu, partant de la on peut bien faire la figure que l'on veut !
#14 - 16-03-2011 23:07:00
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 378
Echecss 9
C'est possible : les petits dessins ci-dessous l'expliquent mieux qu'un long discours :
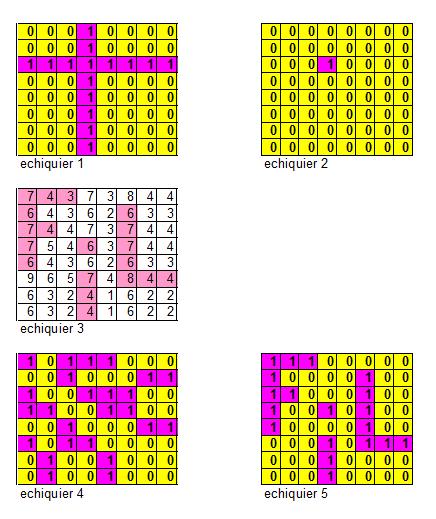
On remarque tout d'abord 2 propriétés des retournements :
l'ordre dans lequel on les effectue n'a pas d'importance,
faire 2 retournement à partir de la même case revient à ne rien faire, donc chaque case sera choisie 0 ou 1 fois.
Sur l'échiquier 1, j'ai noté les cases dont je retourne la ligne et la colonne avec un 1, les autres avec O. Le résultat est l'échiquier 2 : on peut donc retourner une seule case où on veut. Cela nous permet donc d'affirmer que l'on peut atteindre la figure finale, puisque l'on est capable de retourner individuellement chaque case.
Sur l'échiquier 3, j'ai donc noté sur chaque case le nombre de cases de la colonne ou de la ligne qui sont retournés.
Ensuite, j'ai mis sur l'échiquier 4, 1 quand ce nombre était impair et 0 quand il était pair.
Celà me définit les cases dont il faut retourner les lignes et les colonnes pour obtenir l'échiquier 5. Et voilà !
METHODE PLUS RAPIDE
On peut faire plus vite, avec le même formalisme pour trouver l'échiquier 4, en effet, il suffit de remarquer que l'échiquier 1 donne le 2 mais que, aussi, l'échiquier 2 donne le 1... et c'est vrai pour tous les échiquiers...
Donc on prend l'image de "FIL" échiquier 5 recherché qui nous donne le 4.
#15 - 17-03-2011 10:45:47
- debutant1
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 116
checs 9
Étudions le cas général.
Soit un rectangle a lignes , b colonnes.
Soit Li l'opérateur qui modifie la ligne i.
Soit Cj " " " " " " j.
Tous dessin correspond à une suite d'opérateur : Li..CJ..Lk.
On vérifie que l'ordre n' a pas d'importance (commutativité), et que chaque opérateur est unique ( car deux fois le même opérateur revient à l'opération nulle).
Soit une suite quelconque d'opérateur O=Li...Cj... l le nombre d'opérateurs Li et c le nombre d'opérateurs Cj.
Lorsqu'on étudie le dessin constitué avec la suite d'opérateur O on remarque que pour chaque ligne le nombre de carrés blancs est égal soit à b-c soit à c.
de même pour les colonnes, le nombre de carré blanc est soit a-l ou l .
Sur le dessin on vérifie que les lignes ont 4, 5 ,6 carrés blancs. donc on ne peut pas faire ce dessin avec les opérateurs Li et Cj.
Cette condition est nécessaire mais pas suffisante.
Prenons les lignes qui comptent b-c carrés blancs. Ceux ci forment une famille FL(b-c). De même les carrés blancs des lignes qui comportent c carrés blancs forment la famille FL(c). Nous faisons de même pour les colonnes .
nous avons aussi les familles FC(a-l) et FC(l).
La condition nécessaire et suffisante pour réaliser un dessin dans le rectangle est que la famille FL(b-c) soit confondue avec une des deux familles FC(a-l) ou FC(l) et la famille FL(c) avec l'autre famille FC(l) ou FC(a-l)
#16 - 17-03-2011 16:14:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Echeecs 9
Bonnes réponses de Bamby2 et Dylasse 
Débutant répond bien au premier problème ( qui est beaucoup plus simple ) .
Vasimolo
#17 - 17-03-2011 17:34:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
checs 9
Retourner tous les éléments de la ligne et de la colonne d'une case n'est pas équivalent à retourner tous les éléments de la ligne de la case puis tous les éléments de la colonne de la case 
Vasimolo
#18 - 17-03-2011 20:24:43
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Echeecs 9
Premier problème simple : on ne peut pas retourner 19 pions en les retournant 8 par 8, le nombre de pions rouges demeurant pair à chaque coup joué.
Second problème : pris note, chaque retournement concerne une ligne ET une colonne, soit 15 pions.
La parité du nombre de pions rouges, qui est la même que le nombre de retournements de pions, change à chaque fois qu'on retourne un pion.
Pour avoir 19 pions rouges à la fin (le motif), il faut donc jouer un nombre impair de fois.
(A suivre)
EDIT Battu par l'horloge.
#19 - 19-03-2011 12:45:20
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Ececs 9
Grrr... à mon tour de mériter une fessée déculottée  J'ai pas cru que c'était possible et j'ai regretté ne pas avoir un jeu d'othello sous la main. J'ai pas cru que c'était possible et j'ai regretté ne pas avoir un jeu d'othello sous la main.
#20 - 19-03-2011 13:01:04
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
rchecs 9
J'ai aussi été battu par l'horloge 
The proof of the pudding is in the eating.
#21 - 19-03-2011 13:14:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#22 - 19-03-2011 13:24:53
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
echrcs 9
C'est surtout que le WE commence aujourd'hui...
The proof of the pudding is in the eating.
#23 - 19-03-2011 15:34:19
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
Ecchecs 9
Si j'avais cru que c'était possible, j'aurais sûrement pensé à un moment où à un autre à chercher à retourner un seul pion, après c'est une question de temps et de penser au bon truc au bon moment 
Ne change rien, c'était parfait !
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









