Bonsoir,

J'ai trouvé Ausser = 40%, Bordo = 45% et Caley = 15%

Les équations :
P(B) = P(A) + P(C)/3 car on est à Bordeaux à chaque fois qu'on vient d'Ausser et une fois sur trois après Caley.
P(C) = P(B)/3 car on est à Caley une fois sur trois après Bordo.
P(A) + P(B) + P(C) = 1 car il faut bien être quelque part !

Klim.

A= 40%
B= 45%
C= 15%

nb On n'a pas besoin de supposer les probabilités initiales.

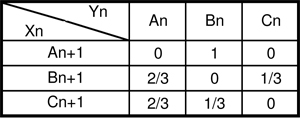
Je note [latex]a_n, b_n, c_n[/latex] les probabilités au jour n de vendre dans les villes d'Ausser, Bordo, et Caley. Je note les évènements associés [latex]A_n, B_n,C_n[/latex]

On peut regrouper les données de l'énoncé dans le taleau suivant, où chaque case vaut la probabilité [latex]P(X_n/Y_n)[/latex]



On en déduit les 3 relations de récurrence suivantes :
[TeX]
\left {
\begin{array}{ccc}
a_{n+1} & = & \frac23b_n+\frac23c_n \\
b_{n+1} & = & a_n+\frac13c_n \\
c_{n+1} & = & \frac13b_n \\
\end{array}
[/TeX]
On introduit alors la matrice A :
[TeX]
A=\left (
\begin{array}{ccc}
0 & \frac23 & \frac23 \\
1 & 0 & \frac13 \\
0 & \frac13 & 0 \\
\end{array}
\right )
[/TeX]
et le vecteur [latex]V_n[/latex] :
[TeX]
V_n=\left (
\begin{array}{ccc}
a_n \\
b_n \\
c_n \\
\end{array}
\right )
[/TeX]
Les relations de récurrence se mettent sous la forme
[TeX]V_{n+1}=A.V_n[/TeX]
Si on veut trouver les probabilités limites (quand le nombre de jours tend vers l'infini), on cherche un vecteur constant V vérifiant :
[TeX]V=A.V[/TeX]
On trouve :
[TeX]
V=\left (
\begin{array}{ccc}
\frac25 \\
\frac9{20} \\
\frac3{20} \\
\end{array}
\right )
[/TeX]
Si on veut trouver les probabilités en fonction de n, c'est un peu plus compliqué.

La matrice A a pour valeurs propres (je passe les calculs) :
[TeX]\lambda_1=1
\lambda_2=-\frac23
\lambda_3=-\frac13
[/TeX]
On peut diagonaliser la matrice, avec matrice de passage et tout le toutim, ou alors on peut utiliser le fait que chacune des suites [latex]a_n,b_n,c_n[/latex] vérifie alors une relation de la forme :
[TeX]x_n=x_1+x_2.(-\frac23)^n+x_3.(-\frac13)^n[/TeX]
où [latex]x_1,x_2,x_3[/latex] sont des constantes

Après quelques calculs, on aboutit à la forme finale :
[TeX]
\left {
\begin{array}{ccc}
a_{n} & = & \frac25-\frac1{15}(-\frac23)^n \\
b_{n} & = & \frac9{20}+\frac2{15}(-\frac23)^n-\frac14(-\frac13)^n \\
c_{n} & = & \frac3{20}-\frac1{15}(-\frac23)^n+\frac14(-\frac13)^n \\
\end{array}
[/TeX]
Et on retrouve bien les valeurs limites !

En effet, Mathias, une petite chaîne de Markov...
Vos solutions, bien que différentes, amènent toutes à la même bonne réponse. Bravo à vous ! J'ai essayé d'en trouver une inédite... qui laisse un peu de côté "matrice de transition" et "diagonalisation".

On peut chercher le vecteur de probabilité (composantes positives et somme des composantes égale à 1) qui est vecteur propre de la transposée de P pour la valeur propre 1 : c'est ce qu'on appelle le vecteur de probabilité constant. On trouve facilement le vecteur , qui s'interprète de la même façon : Jean-Pierre passe 40 jours sur 100 dans la ville d'Ausser, 45 jours sur 100 dans la ville de Bordo et 15 jours sur 100 dans la ville de Caley. Cette méthode a l'avantage d'être rapide. Elle ne nécessite pas une diagonalisation complète de P.