C'est pas une blague j'espère ?
Bon je commence mais je ne suis pas sur de trouvé quelque chose

A vu de nez je dirai au alentour de 1/9 mais je ne vie pas dans la ville de Grasse, j'ai pas un bon flaire

Sauf erreur [latex]\frac {\pi-2\sqr2+2+\arccos {\frac 1 3}}{9\pi}\approx\,0.1253477787[/latex]

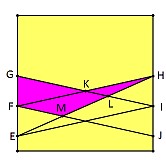
Je ramène le problème à ce dessin plus simple (en présupposant que les courbes sont bien parallèles et symétriques).

Une bande oblique courbe a la même aire qu'une bande oblique droite et qu'un rectangle (l'inclinaison n'a pas d'influence sur l'aire) : 2/9 du carré.

Les deux grandes aires roses peuvent s'assembler pour former la moitié d'une telle bande : 1/9 du carré

Le petit triangle rose a 1/3 de la base et 1/2 de la hauteur de EFH qui vaut également une demi-bande : (1/9):6 = 1/54 du carré

L'aire rose vaut donc 1/9 + 1/54 = 7/54 de l'aire du carré.

Je crois que mon raisonnement n'est pas bon pour la petite pointe rose en haut à droite

Les courbes ressemblent à des sinus/cosinus ou même à des arctangentes sans que rien ne permette d'en être sûr et rien non plus ne permet de penser que toutes les courbes sont du même type. Or la solution me semble dépendante du type de courbes.

Dès lors est-il possible d'avoir un peu plus d'explications ?

Le problème est sympa, c'est dommage de ne pas pouvoir avancer.

Merci pour l'indice par MP!

Avec cette indice, je peux supposer d'avantage qu'il s'agit de fonction cosinus.



Je prend d=1.

f(x) = 2 - cos(x)
g(x) = 3 - 2 cos(x)
h(x) = 2 + cos(x)
i(x) = 4 - cos(x)

J'ai besoin des abscisses des intersections entre d'une part g(x) et h(x) et d'autre part entre f(x) et h(x).

g(x) = h(x)
3 - 2 cos(x) = 2 + cos(x)
cos(x) = 1/3
x = 1.231 = a

f(x) = h(x)
2 - cos(x) = 2 + cos(x)
cos(x) = 0
x = pi/2

Ce qui donne:
[TeX]Aire 1 + Aire 2\\
=\int_{0}^{a}(i(x) - h(x))dx + \int_{a}^{\pi }(i(x) - g(x)) dx\\
=2\int_{0}^{a}(1 - cos(x))dx + \int_{a}^{\pi }(1 + cos(x)) dx\\
=2\left [ x-sin(x)\right ]_{0}^{a}+\left [ x+sin(x)\right ]_{a}^{\pi }\\
=2(a-sin(a))+ \pi-a-sin(a)\\
= 1,541249[/TeX]
et
[TeX]Aire 3\\
=\int_{\pi /2}^{\pi}(f(x) - h(x))dx \\
=\int_{\pi /2}^{\pi}(2 - cos(x) - 2 - cos(x))dx \\
=\int_{\pi /2}^{\pi}-2 cos(x)dx \\
= 2[sin(x)]_{\pi}^{\pi/2}\\
= 2[/TeX]
d'où

Aire 1 + Aire 2 + Aire 3 = 3,541249
Aire totale = 9pi

La pourcentage d'aire rose vaut donc 12,52%.

J'étais pas si loin avec mes segments de droites. ^^

Ahh, qu'est ce que j'aime les énigmes dont tous les éléments nécessaires sont dans l'énoncé !

@Cédric: que manquait-il ?  Deux ont réussi à résoudre ce problème.
@Kosmogol: évite de venir dans un topic pour emmener sur un des tiens, c'est assez détestable !

@Saint-Pierre : juste le fait que l'on pouvait se permettre d'approximer visuellement les courbes du dessin par des fonctions particulières. Je ne trouve pas cela très propre (du point de vue du raisonnement mathématique) mais ce n'est que mon avis !

SaintPierre a écrit:

@Cédric: que manquait-il ?  Deux ont réussi à résoudre ce problème.

Là, je me permet de te contredire. J'ai eu exactement le même problème que les autres. C'est par MP que tu m'as suggéré qu'il fallait utiliser des cosinus. J'ai joué le jeu mais rien dans l'énoncé ne permet d'affirmer qu'il s'agit bien de cosinus.

Halloduda entend les voix du seigneur , ou de l'un de ses saints , il est donc le seul à échapper à l'apocalypse

En l'état le problème n'est toujours pas complet , on entend seulement certains dire qu'il ont eu des indices,  via MP , parlant de cosinus .

Bref , c'est pas sérieux et il ne faut vraiment pas s'étonner qu'il y ait si peu de bonnes réponses

Vasimolo

Pas la peine de t'énerver contre lui, il est parti de toute façon...

MthS-MlndN a écrit:

Pas la peine de t'énerver contre lui, il est parti de toute façon...

Pourquoi est-il parti?

Et alors ? C'est bien de se moquer.