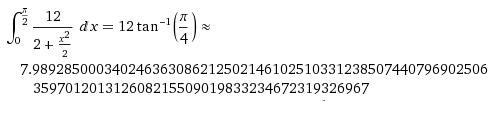Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 27-07-2011 18:42:14
Gagenr une glace au resto.Aujourd'hui dans un petit restaurent ou je suis allé manger en famille un serveur qui travaillait pendant les vacances et qui faisait des classes prépa proposait une glace payé de sa poche contre la réponse à : "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#0 Pub#2 - 27-07-2011 18:47:26#3 - 27-07-2011 18:52:55#4 - 27-07-2011 18:57:54
Gagner ue glace au resto.Le pauvre en vacances il a de DM à faire "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #5 - 27-07-2011 19:06:07#6 - 27-07-2011 19:13:33#7 - 27-07-2011 19:49:43#8 - 27-07-2011 19:53:40
Gagner une glace u resto.12 ! #9 - 27-07-2011 19:55:43#10 - 27-07-2011 20:26:39#11 - 27-07-2011 20:31:10
Gagne rune glace au resto.Au fait, je hais ce point à la place de la virgule... J'ai cru que je disais une idiotie. C'est un peu comme l'orthographe, ça dérange je trouve.
#12 - 27-07-2011 20:38:13
Ganer une glace au resto.Alors... On pose I la bête. #13 - 27-07-2011 20:41:46#14 - 27-07-2011 22:48:52
gagner une flace au resto.Bonsoir #15 - 28-07-2011 14:28:25
Gagner une glace au ersto.\int_0^{\pi/2}{24\over{4+x^2}dx}=\frac{24}{2}\int_0^{\pi/2}{1\over{2(1+(\frac{x^2}{2})}dx}=\frac{24}{2}[arctan(\frac{x}{2})]_0^{\pi/2}=\frac{24}{2}arctan(\frac{\pi}{4})=12 #16 - 28-07-2011 14:30:39
Gagne une glace au resto.@gabrielduflot tu n'as pas gagné de glace, pourtant tu étais bien parti "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #17 - 28-07-2011 19:03:52#18 - 28-07-2011 19:19:47#19 - 28-07-2011 21:14:54
gafner une glace au resto.La derivee d'arctan serait plutot de niveau terminal que de classe prepa, non? The proof of the pudding is in the eating. #20 - 28-07-2011 21:20:04
aGgner une glace au resto.Mon prof de maths m'a dit que l'étude des fonctions réciproques on ne la fait pas au lycée. "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #21 - 28-07-2011 21:20:15
Gagne une glace au resto.C'est effectivement du niveau de la terminale. Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.