 |
#1 - 06-07-2012 23:20:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dés
Bonsoir
Un problème proposé par Clydevil en prolongement des dés 4 et 5 
On construit un cube avec 27 petits cubes blancs et on peint toutes ses faces en rouge . On détruit le cube et on le reconstruit de façon à ce que toutes ses faces soient blanches et on les peint à nouveau en rouge .
Avec ces 27 cubes peut-on encore reconstruire un cube dont toutes les faces sont blanches ???
Amusez-vous bien 
Vasimolo
#2 - 07-07-2012 00:15:02
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
sés 6
Il y a 54 faces visibles sur le grand cube, pour 162 faces en tout (27 dés, 6 faces par dé), soit pile le triple. Si c'est possible, ça rentre juste.
Quelques grattages de papier plus tard : bah ouais, ça rentre. En écrivant entre parenthèses, pour chaque dé ou type de dé du troisième cube (tout blanc), le nombre de faces peintes lors de la peinture du premier cube, puis lors de la peinture du deuxième cube, sous la forme (x+y) :
Le dé central a été dé d'angle les deux fois précédentes (3+3), chacun des six centres de faces a été une fois dé d'angle et une fois dé de milieu d'arête (3+2), six des 12 dés de milieu d'arête ont déjà été à la même place les deux fois précédentes (2+2), les six autres ont été une fois sur un angle et une fois en centre de face (3+1), six des 8 dés d'angle ont été une fois en centre d'arête et une fois en centre de face (2+1), les deux qui restent ont été une fois en angle et une fois au centre du cube (3+0).
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#3 - 07-07-2012 07:20:58
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
sés 6
On commence par un petit calcul pour ne pas se fatiguer inutilement :
54 faces colorées à chaque fois , soit 108.
Les cubes totalisent 6 x 27 = 162 faces. Il en reste 54, ça peut peut-être passer...
Et ça passe ! 
Mais il faut faire attention à l'orientation des cubes la seconde fois. pour que 2 faces + 2 faces colorées en laissent 2 adjacentes et non opposées par exemple.
Allez, un petit tableau pour expliquer comment :
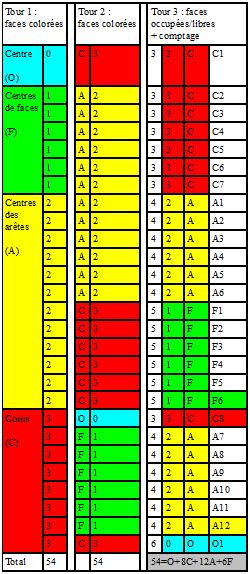
#4 - 07-07-2012 07:57:41
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Dés
Bonjour,
Au premier coup de peinture, les petits cubes situés aux huit sommets du grand cube auront trois faces rouges. Si à la reconstruction, l'un (ou plusieurs) de ces huit petits cubes se retrouvent de nouveau sur un sommet avec une orientation toute blanche, alors au second coup de peinture ce (ou ces) petits cubes auront six faces rouges et il sera alors impossible (sauf si ce petit cube unique rouge se retrouve à l'intérieur) de reconstruire un grand cube blanc.
Bonne journée.
#5 - 07-07-2012 09:39:11
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
fés 6
Le cube contient 27 dés de 6 faces.
les faces extérieures du cube peint sont au nombre de 6x9=54
on repeint à nouveau 54 faces blanches et il reste exactement 54 faces non peintes.
Peuvent-elles etre toutes sur l'exterieur? reciproquement, peut-on avoir toutes les faces cachées peintes en rouge?
le cube interieur est un coin peint deux fois,
les 6 centres de face ont un seul blanc et 5 rouges donc furent une arête puis un coin ou inversement,
les 8 coins (3 rouges et 3 blancs) furent 4 faces puis 4 aretes ou inversement,
les 12 aretes (4 rouges et 2 blanc) furent deux fois arêtes ou face/coin.
Cela laisse pas mal de possibilités pour que la construction soit possible, donc très probablement oui. Je vais en chercher une...
The proof of the pudding is in the eating.
#6 - 07-07-2012 11:27:06
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
és 6
La réponse est oui, si à la 2eme repeinture on prend soin de choisir quelles sont les faces que l'on positionnent dans quels emplacement précis.
Voici une solution:
3 représente les 3 faces peintes dans un coin (et il y a 8 coins)
2 représente les 2 faces peintes sur un bord (et il y a 12 bords)
1 représente la face peinte dans le milieu d'une face (et il y a 6 centres de face)
0 représente le petit cube au centre du grand cube. (et il y a 1 seul milieu)
De gauche à droite sont les 3 arangements de cubes:
3 - 2 - 1
3 - 2 - 1
3 - 2 - 1
3 - 2 - 1
3 - 2 - 1
3 - 2 - 1
2 - 2 - 2
2 - 2 - 2
2 - 2 - 2
2 - 2 - 2
2 - 2 - 2
2 - 2 - 2
2 - 1 - 3
2 - 1 - 3
2 - 1 - 3
2 - 1 - 3
2 - 1 - 3
2 - 1 - 3
1 - 3 - 2
1 - 3 - 2
1 - 3 - 2
1 - 3 - 2
1 - 3 - 2
1 - 3 - 2
0 - 3 - 3
3 - 0 - 3
3 - 3 - 0
horizontalement la somme de tous les chiffres fait 6, donc toutes les faces de chaque cube peuvent etre peintes en 3 arangements.
Notez egalement:
- que 27 cubes * 6 faces font exactement 162 faces a peindre.
- que le grand cube a 9*6 soit 54 faces exposées, 3 fois de suite, soit 162 faces également.
- que pour la sequence 2 - 2 - 2, il faut egalement prendre soin de laisser les 2 dernieres faces non peintes de maniere a ce quelle se touchent (ne pas peindre 4 faces en couronne autour du sube) sinon on ne pourrais pas ré-arranger le cube pour l'étape finale.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#7 - 07-07-2012 12:04:08
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Déés 6
C'est impossible !
Un petit dessin avec les liens possibles, 6 essais de répartition, tous échouent.
#8 - 07-07-2012 12:13:09
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dés
Que des bonnes réponses 
On peut aussi reformuler le problème de la façon plus distrayante :
Les faces de 27 cubes sont astucieusement colorées en rouge , vert ou bleu . Peut-on envisager trois assemblages de ces cubes ne laissant apparaître que des faces rouges , que des faces vertes , que des faces bleues ?
Vasimolo
@Nodgim : cherche un peu plus 
#9 - 07-07-2012 15:08:10
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1015
Dés 66
En réponse au problème initial, et en espérant que cette présentation soit compréhensible, j'arrive à ceci:

http://www.prise2tete.fr/upload/elpafio-Des6.PNG
Avec ces 27 petits cubes, on peut au final encore reconstruire un grand cube dont toutes les faces sont blanches.
Merci Vasimolo 
#10 - 08-07-2012 08:03:08
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Dé 6
Ah ben oui si on oublie le dé central....
-8 emplacements de sommet S
-12 emplacements de milieu d'arête A
-6 emplacements de milieu de face F
-1 emplacement central C
On peut réaliser 9 boucles indépendantes de 3 emplacements.
6 boucles S--->F---->A
<----------
1 boucle S---->C---->S
<------------
2 boucles A---->A---->A
<------------
Et on a bien fait tourner tous les dés. La somme des faces peintes de chaque dé est exactement de 6 après 3 séquences de coloriage.
C'était une question très originale, bravo au concepteur.
#11 - 08-07-2012 08:54:00
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
éDs 6
Zut, j'arrive en retard.
Oui--)27 cubes, 6 faces par cubes=162 faces
Maintenant, 2 fois la couleur rouge+1 fois le blanc=3
162/3=54
6 faces
54/6=9
9 faces apparentes sur chaque grande face, c'est gagné!
Un promath- actif dans un forum actif
#12 - 09-07-2012 19:52:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
éDs 6
Je n'ai pas tout compris Promath 
Vasimolo
#13 - 09-07-2012 23:31:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dé 6
Une belle idée de Clydevil 
Un jeu de cubes tricolores que je proposerais volontiers aux classes primaires !
Merci aux participants 
Vasimolo
#14 - 09-07-2012 23:50:06
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
#15 - 10-07-2012 12:55:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#16 - 10-07-2012 13:02:38
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
Dsé 6
Je serais même tenté de dire qu'on peut le faire n fois pour un cube de dimension n
1 : 1 fois
2 : 2 fois
3 : 3 fois
4 : 4 fois ?
#17 - 10-07-2012 13:34:29
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
éDs 6
je dirais plutot:
2: 1 fois
3 : 3 fois
4 : 9 fois
puisque un tesseract a 24 faces, un petit cube a donc 24 faces, et un grand cube a 24*9 faces = 216.
il y a 81 petits cubes dans un tesseract ce qui nous fait au total 81*24 = 1944 faces a peindre.
et 1944 / 216 = 9
Je crois qu'un grand tesseract ainsi decoupé a trois err... un certain nombre de petits tesseracts non visibles.
A moins qu'on divise chaque face en 16 petits carrés au lieu de 9.
PS: Vous m'excuserais si je ne fais pas de dessin... faire du 4-dimensions en 2 dimensions ca ne marche pas tres bien...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#18 - 10-07-2012 13:44:08
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,996E+3
#19 - 12-07-2012 04:41:07
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
déd 6
oui effectivement, j'avais mal compris... des qu'on parle de "dimensions" je pense aussitot "dimensions"... 
Ceci dit, ca vaut bien un nouveau sujet
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#20 - 12-07-2012 19:08:15
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Dé 6
Gwen, peut être avec la manière dont j'ai traité le problème, par le biais de boucles, ça serait possible de trouver une preuve formelle.
Cube de coté n----> boucles de longueur n.
#21 - 14-07-2012 12:15:32
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Déés 6
La preuve pour n>=6.
On désigne les emplacements des dés par le nombre de faces extérieures: 0,1,2 ou 3.
Pour n>=6, on dénombre:
dé0=(n-2)^3
dé1=6(n-2)²
dé2=12(n-2)
dé3=8
On construit des boucles. Une boucle est représentée par n chiffres compris entre 0 et 3, chiffres qui correspondent aux emplacements des dés dans le cube. Dans une boucle donnée, chaque position de chiffre correspond à une couleur. Chaque dé au rang k prendra successivement les positions k, k+1, k+2, ..n, 1, 2, ...k-1.
La somme des chiffres d'une boucle vaut 6: correspond aux 6 faces peintes de chaque dé.
Exemple pour n=6, on fait tourner 6 dés:
330000
Ainsi, le dé en 1ère position est dans un angle, on lui peint 3 faces, ensuite le même dé passe en 2ème position, on lui peint les 3 autres faces, ensuite pour les 3 à 6 èmes positions, il est en 0, à l'intérieur, on lui peint 0 faces. Même démarche pour les 5 autres dés.
Nombre de faces pour un cube de coté n= 6n^3
Nombre de faces visibles: 6 n²
Nombres de couleurs: 6n^3/6n²=n
Boucles de n dés à établir:
4 boucles 33000.. (n-2) zéros
4(n-2) boucles 222000.. (n-3) zéros
(n-2)² boucles 1111110000...(n-6) zéros
Nombre de dé3: 4*2=8
Nombre de dé2: 4(n-2)3=12(n-2)
Nombre de dé1: 6(n-2)²
Nombre de dé0=4(n-2)+4(n-2)(n-3)+(n-2)²(n-6)=(n-2)^3
Avec ces boucles, on retrouve bien les n^3 dés.
CQFD
#22 - 14-07-2012 18:42:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dé s6
@Nodgim
J'ai bien lu tes explications mais je n'arrive pas à comprendre ton idée : c'est sûrement de ma faute 
Vasimolo
#23 - 14-07-2012 20:00:54
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Déss 6
L'idée est de choisir judicieusement des groupes de n dés, qui resteront inchangés pendant toute l'opération de coloriage, chaque dé d'un groupe est relié fictivement à ses voisins comme les perles d'un collier . On peint une 1ère fois le cube. Ensuite, on va faire un décalage d'une position de chaque dé de chaque groupe, de sorte que chacun d'eux prenne la position de son voisin dans chaque collier. On peint alors une seconde fois le nouveau cube obtenu et on recommence l'opération "décalage".
Bien entendu, à l'intérieur d'un groupe de n dés, la somme des faces doit être exactement de 6. Ainsi, en faisant décaler n fois les dés du collier, on aura peint à la fin 6n faces, donc toutes les faces de tous les dés du collier.
#24 - 15-07-2012 09:53:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dé 6
Bon , j'ai compris le principe et c'est plutôt très malin:)
Je reformule pour voir si on est d'accord !
Il y a trois types de chaînes , toutes de longueur [latex]n[/latex] .
Type S :SSII...II : 4 chaînes en tout .
Type A :AAAII...II : 4(n-2) chaînes en tout .
Type F :FFFFFFII...II : (n-2)² chaînes en tout .
On retrouve bien les [latex]n^3[/latex] petits cubes .
Maintenant comment faire tourner les cubes dans les chaînes pour laisser apparaître les [latex]n[/latex] couleurs .
Initialement on voit 2 , 3 ou 6 cubes de chaque chaîne ( les autres sont à l'intérieur du grand cube ) . On peint toutes les faces visibles dans la première couleur et on fait apparaître les couleurs suivantes ?
Couleur 2 : on fait tourner tous les cubes apparent et on peint .
Couleur 3 : on fait tourner tous les cubes de type A et F , on avance de 2 rangs dans les chaînes de type S et on peint .
Couleur 4 : on fait tourner tous les cubes de type F et S , on avance de 3 rangs dans les chaînes de type A ...
Couleur 5 : on fait tourner tous les cubes de type F et A , on avance de 2 rangs dans les chaînes de type S ...
Couleur 6 : on fait tourner tous les cubes apparent ...
Couleur 7 : on avance de 2 , 3 ou 6 rangs dans les chaînes de type S , A ou F ...
et ainsi de suite .
On voit que les boucles ne se referment correctement que si [latex]n[/latex] est un multiple de 6 .
Y-a-t-il moyen de modifier le modèle pour le faire coller aux autres cas ?
Vasimolo
#25 - 15-07-2012 12:03:48
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
déq 6
Attention, initialement, il y a 2,3 ou 6 cubes apparents, selon les types de chaine. Et ce n'est pas initialement que ça passe, c'est à chaque opération de coloriage. Seulement, ce sont à chaque fois des cubes différents qui viennent prendre la place du précédent selon l'ordre établi dès le départ par le chainage.
En fait la démonstration se fait sur une seule chaine, et ensuite il ne reste plus qu'à prouver qu'on peut affecter à chaque cube une seule chaine.
J'ai généralisé à partir de n=6 parce qu'on peut dans ce cas grouper les cubes qui ne présentent qu'une seule face, c'est à dire mettre 6 cubes extérieurs dans une chaine.
Sinon, pour les cas n=4 et n=5, ça ne pose aucun problème particulier.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum






