 |
#1 - 20-05-2011 08:15:14
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Dés truuqés
C'est une énigme due à Halmos P.
Est-il possible de truquer deux dés, de manière différente si on le souhaite, pour que la probabilité d'apparition de chaque somme possible de 2 à 12 (total de ce qui apparaît sur le premier et deuxième dé après un lancé simultané) soient les mêmes?
(Je n'ai pas pu vérifier toutes les énigmes sur les dés proposées.)
Un mathématicien complet est topologiquement fermé!
#2 - 20-05-2011 11:13:19
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
fés truqués
Bonjour,
Même en truquant les dés, on a 6 x 6 = 36 sommes possibles.
Pour que les apparitions soient équiprobables (de 2 à 12 = 11), il faudrait que 36/11 soit un entier, ce qui n'est pas le cas.
Je pense donc que c'est impossible.
Bonne journée.
Frank
#3 - 20-05-2011 11:33:57
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
Dés truquéés
Soit A et B les deux dés, Ai les probabilités d'obtenir i avec le dé A et Bi la probabilité d'obtenir i avec le dé B. Il y a donc 12 inconnues
On a un système de 13 équations, une pour chaque somme ( de 2 à 12) et une pour chaque dé.
On a donc un système de 13 équations et 12 inconnues.
A1 + A2 + A3 + A4 + A5 + A6 = 1
B1 + B2 + B3 + B4 + B5 + B6 = 1
A1.B1 = 1/36
A1.B2 + A2.B1 = 2/36
A1.B3 + A2.B2 + A3.B1 = 3/36
A1.B4 + A2.B3 + A3.B2 + A4.B1= 4/36
A1.B5 + A2.B4 + A3.B3 + A4.B2 + A5.B1= 5/36
A1.B6 + A2.B5 + A3.B4 + A4.B3 + A5.B2 + A6.B1 = 6/36
A2.B6 + A3.B5 + A4.B4 + A5.B5 + A6.B2 = 5/36
A3.B6 + A4.B5 + A5.B4 + A6.B5 = 4/36
A4.B6 + A5.B5 + A6.B4 = 3/36
A5.B6 + A6B5 = 2/36
A6.B6 = 1/36
Voilà, j'ai une équation en trop. Et comme le problème est symétrique, j'ai peur que si j'ai une équation en trop, j'en ai au moins deux en trop et je resterai alors avec un problème avec plus d'inconnues que d'équation. ceci impliquerai une possible multiplicité dans les probabilités possibles.
Je regarderai ça plus en profondeur quand j'aurai plus de temps.
Je pense que je peux montrer qu'il y a 12 équations indépendantes, mais je sais pas encore comment.
#4 - 20-05-2011 11:36:02
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
déd truqués
Bonjour,
Prenons des dés "traditionnels" cubiques numérotés de 1 à 6

On notera aussi (voir photo) que cette définition "traditionnelle" suppose :
- que les faces 1,2,3 et 4,5,6 se touchent par un coin
- leur orientation (ici dans le sens inverse des aiguilles d'une montre)
- que la somme des faces opposées est toujours égale à 7
La meilleure réponse que j'obtiens pour l'instant donne encore une probabilité double d'obtenir 7 dans une série de 2 à 12 :
Avec de tels dés, si nous induisons "juste" un balourd égal sur la face "1" et la face "6" d"un dé, un tirage avec un deuxième dé "normal" donnera : 2,3,4,5,6,7,7,8,9,10,11,12
Bof:/ , donc si la solution existe, il faut proposer mieux !
Mes idées pour truquer les dés sont :
Lestage
- d'un coin / de plusieurs coins
- d'une arête / de plusieurs arêtes
- d'une face / de plusieurs faces
et/ou
Variantes de numérotation
Je suppose qu'il faut garder une numérotation de 1 à 6 sur chaque dé (sinon le trucage serait flagrant)
En revanche, on peut certainement (si utilité quelconque) déroger à la présentation "traditionnelle" (= faces adjacentes, orientation, sommes des faces opposées différentes de 7 ..)
....
A suivre !
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#5 - 20-05-2011 11:52:29
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Dés truqué
J'ai posé le problème mathématiquement je ne me suis pas demander si physiquement c'est réalisable avec du plomb reparti dans un cube.
Un mathématicien complet est topologiquement fermé!
#6 - 20-05-2011 12:19:00
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Dés trruqués
Si je suppose que la probabilité qu'un dé donne k est égale à la probabilité que l'autre dé donne 7-k, je vais aboutir ?
J'ai ainsi 6 équations à 5 inconnues, si la solution existe elle est unique.
En notant [latex]a_k[/latex] la probabilité que le premier dé donne k :
[TeX]a_1a_6[/TeX]
[TeX]=a_1a_5+a_2a_6[/TeX]
[TeX]=a_1a_4+a_2a_5+a_3a_6[/TeX]
[TeX]=a_1a_3+a_2a_4+a_3a_5+a_4a_6[/TeX]
[TeX]=a_1a_2+a_2a_3+a_3a_4+a_4a_5+a_5a_6[/TeX]
[TeX]=a_1^2+a_2^2+a_3^2+a_4^2+a_5^2+a_6^2[/TeX]
[TeX]=\frac1{11}[/TeX]
et bien sûr [latex]a_1+a_2+a_3+a_4+a_5+a_6=1[/latex]
#7 - 20-05-2011 12:34:56
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Dés truqué
En gros, on veut une loi de probabilité pour le dé A, c'est-a-dire des probabilités [latex]p^A_i[/latex] pour [latex]i \in \{ 1 ; \dots ; 6 \}[/latex] de tomber sur chaque face, telles que [latex]\sum_{i=1}^6 p^A_i = 1[/latex] bien sûr, et de la même façon les probas [latex]p^B_i[/latex] des faces du dé B, soumises bien sûr a la même contrainte de somme, telles que les probas de la somme des deux dés soient toujours les mêmes :
[TeX]p^A_1 p^B_1 = \frac1{36}[/TeX]
[TeX]p^A_1 p^B_2 + p^A_2 p^B_1 = \frac2{36}[/TeX]
[TeX]p^A_1 p^B_3 + p^A_2 p^B_2 + p^A_3 p^B_1 = \frac3{36}[/TeX]
[TeX]p^A_1 p^B_4 + p^A_2 p^B_3 + p^A_3 p^B_2 + p^A_4 p^B_1 = \frac4{36}[/TeX]
[TeX]p^A_1 p^B_5 + p^A_2 p^B_4 + p^A_3 p^B_3 + p^A_4 p^B_2 + p^A_5 p^B_1 = \frac5{36}[/TeX]
[TeX]p^A_1 p^B_6 + p^A_2 p^B_5 + p^A_3 p^B_4 + p^A_4 p^B_3 + p^A_5 [latex]p^B_2 + p^A_6 p^B_1 = \frac6{36}[/TeX]
[TeX]p^A_2 p^B_6 + p^A_3 p^B_5 + p^A_4 p^B_4 + p^A_5 p^B_3 + p^A_6 p^B_2 = \frac5{36}[/TeX]
[TeX]p^A_3 p^B_6 + p^A_4 p^B_5 + p^A_5 p^B_4 + p^A_6 p^B_3 = \frac4{36}[/TeX]
[TeX]p^A_4 p^B_6 + p^A_5 p^B_5 + p^A_6 p^B_4 = \frac3{36}[/TeX]
[TeX]p^A_5 p^B_6 + p^A_6 p^B_5 = \frac2{36}[/TeX]
[TeX]p^A_6 p^B_6 = \frac1{36}[/TeX]
Ca nous fait 13 contraintes pour 12 inconnues ; le fait qu'il y ait au moins une solution (celle où toutes les probas valent [latex]\frac16[/latex]) signifie qu'il y a interdépendance entre les contraintes. On peut ramener ces 13 équations a "seulement" 12. Si on peut les ramener a seulement 11 (voire éventuellement moins), alors il y a une façon de piper les dés qui conserve les probabilités de la somme.
Pas facile...
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#8 - 20-05-2011 12:40:12
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Dés trquués
Il y a de bonnes idées, je dirais ce soir à chacun ce qui ne va pas ou ce qui le bloque.
Un mathématicien complet est topologiquement fermé!
#9 - 20-05-2011 12:48:18
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
Dés ruqués
OK, oublions le trucage "physique", et regardons alors si une numérotation particulière de deux dés permet de répondre à la question :
> il y a 11 sommes de 2 à 12
> un tirage de deux dés cubiques représentent 36 possibilités.
Il faudrait donc un trucage qui donne une probabilité unitaire (de voir apparaitre 2, 3, ....11) de 11/36, mais 11/36 n'étant pas un entier, la réponse est donc "non" !
maintenant, rien dans l'énoncé ne précise que les dés soient cubiques ....!
Il faudrait un dé à 11 faces et un dé quelconque.
Or je ne pense pas qu'il existe d'hendécaèdre (polyèdre à 11 faces) régulier !
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#10 - 20-05-2011 12:56:08
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Dés truqéus
NickoGecko, as tu déjà vu des probabilités entières autres que 0 et 1?
Un mathématicien complet est topologiquement fermé!
#11 - 20-05-2011 13:57:14
- Milou_le_viking
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 446
dés ttuqués
Yanyan a écrit:NickoGecko, as tu déjà vu des probabilités entières autres que 0 et 1?
Oui, pour des très grandes valeurs de 1, 1=2.
Mouhahahahaha, j'en peu plus de cette blague débile...
#12 - 20-05-2011 14:05:07
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1968
Dés truuqués
L'idée est d'associer au premier dé 6 valeurs P1, P2, ... , P6, dont la somme fait 1; d'associer au second des valeurs P'1, P'2, ... , P'6 dont la somme fait aussi 1 et enfin de résoudre le système d'équations suivantes
P1*P'1 = 1/11
P1*P'2+P2*P'1 = 1/11
P1*P'3+P2*P'2+P3*P'1 = 1/11
...
Bon, j'ai déjà réussi à vérifier que les deux dés ne sont pas truqués de la même manière (les Pi et les P'i ne peuvent pas être égaux deux à deux).
J'essayerai de résoudre ça un peu plus tard
#13 - 20-05-2011 15:18:21
- Bamby2
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 152
Dé truqués
notons a1..a6 les proba d'obtenir 1..6 avec le 1er dé, et de meme b1..b6 pour le 2eme
alors
P(2) = a1*b1
P(12) = a6*b6
p(7) = a1b6+a2b5+a3b4+a4b3+a5b2+a6b1 = a1b6+a6b1 + X
avec X positif.
or ces trois sommes sont identiques
des deux premières on peut obtenir:
a1=a6b6/b1
b1=a6b6/a1
et
a6= a1b1/b6
b6=a1b1/b6
en reportant
les 2 premières et les 2 secondes dans P(7), on obtient:
p(7) = a6b6(b6/b1+a6/a1) + X = P(12) = a6b6
et
p(7) = a1b1(a1/a6+b1/b6) + X = P(1) = a1b1
pour avoir l’égalité on doit donc avoir
que les deux sommes entre parenthèses soient <1 car X est positif.
or ces deux sommes ne peuvent être en même temps <1,
si a1/a6 est <1 alors a6/a1 ne peut l’être.
ce n'est donc pas possible d'avoir des probabilités égales pour 2, 7 et 12.
EDIT2 avec clarification: il m'avait paru évident que toutes les proba (a1,a2,b1,b6) sont strictement supérieur a zéro, en effet si une proba est égale a zéro, il faudrait que toutes les probas P(2),p(3) ... P(12) le soient pour satisfaire les égalités, or leur somme est égale a 1. donc aucune n'est égale à 0.
#14 - 20-05-2011 17:28:36
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Dés truqqués
Des excuses à NickoGecko dont je n'ai peut-être pas compris l'argument.
Un mathématicien complet est topologiquement fermé!
#15 - 20-05-2011 19:21:37
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Ds truqués
Une petite aide pour MthS-MlndN et Scarta et d'autres:
Ne reconnaissez-vous pas les coefficients d'un polynôme dans vos équations?
Un mathématicien complet est topologiquement fermé!
#16 - 20-05-2011 19:34:33
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Dés truquéss
Très bien pour Bamby2 sauf peut-être des divisions par un éventuel 0!
Un mathématicien complet est topologiquement fermé!
#17 - 20-05-2011 19:41:51
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Dés truqés
Ils sont fous ces matheux 
Bravo, continuez !
http://enigmusique.blogspot.com/
#18 - 20-05-2011 19:51:06
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Dés trqués
Mmh mmh ... Il faut donc décomposer [latex]X^2\frac{X^{11}-1}{X-1}[/latex] en produits de 2 polynomes de degré 6 sur R ? Il doit y avoir des cosinus de racines 11-èmes de l'unité, là-dedans ! Ca sent le calcul bien bourrin 
#19 - 21-05-2011 02:34:07
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Dés rtuqués
Je note [latex]a_k[/latex] les probabilités d'obtenir k+1 pour le premier dé (k entre 0 et 5)
Je note [latex]b_k[/latex] les probabilités d'obtenir k+1 pour le second dé (k entre 0 et 5)
Soient les deux polynômes suivants de degré 5 :
[TeX]A(X)=\sum_{n=0}^5a_nX^n
B(X)=\sum_{n=0}^5b_nX^n[/TeX]
Je calcule le produit A(X)B(X) :
[TeX]A(X)B(X)=\sum_{n=0}^{10}\left(\sum_{k=0}^n a_k b_{n-k}\right)X^n[/TeX]
Les coefficients de ce polynômes sont exactement les probabilités d'obtenir n comme somme des deux dés.
On doit alors trouver deux polynômes A et B, à coefficients réels entre 0 et 1 , vérifiant :
[TeX]A(X)B(X)=\frac{X^{11}-1}{11(X-1)}[/TeX]
C'est impossible !
En effet, les racines 11-èmes de l'unité (sauf 1) sont des complexes non réels. Les polynômes réels divisant [latex]X^{11}-1[/latex] sont donc de degré pair, et on ne peut pas trouver deux polynômes de degré 5 répondant au problème.
La réponse est donc : non 
#20 - 21-05-2011 05:19:24
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1821
dés trusués
Re-bonjour !
Je reformule ....
Dit autrement, il apparaît impossible de distribuer équitablement 11 sommes différentes (entiers de 2 à 12) dans 36 cases (6*6),
11 n'étant pas un diviseur de 36 ...
et ceci quelle que soit la re-numérotation d'un ou des deux dès
Illustrations sans valeurs de démonstration ...
Tirages avec deux dés traditionnels :
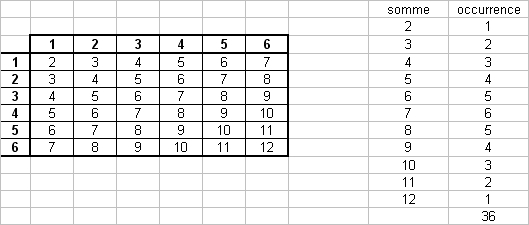
Recherche de trucage : idée avec un dé ayant trois faces "1' et trois faces "6" ....
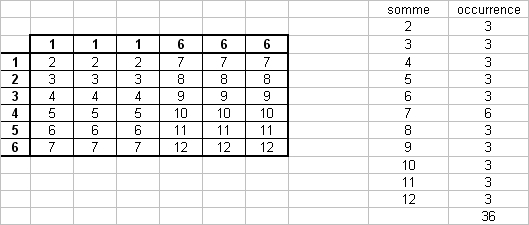
Aussi, tout trucage "physique" (lestage) est également vain, à moins de pouvoir influencer le tirage du second dé en fonction du premier, difficile avec un lancé simultané ...
A suivre ...
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#21 - 21-05-2011 10:40:18
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
DDés truqués
Les probabilités de chacune des 11 sommes serait 1/11.
Donc P(1)=P(6)=[latex]\frac 1 {\sqr {11}}\approx0.30[/latex]
Et P(2)=P(5)=[latex]\frac 1 {2\sqr {11}}\approx0.15[/latex] car il ya deux façons d'obtenir S=3 ou 11
Il reste P(3)=P(4)=[latex]\frac 12-\frac 3 {2\sqr {11}}\approx0.05[/latex]
#22 - 21-05-2011 12:16:21
- ksavier
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 166
déd truqués
Je pense que cela n'est pas possible.
Notons respectivement [latex]a_1,a_2,a_3,...,a_6[/latex] les probabilités d'obtenir 1,2,3,...,6 avec le premier dé.
Notons respectivement [latex]b_1,b_2,b_3,...,b_6[/latex] les probabilités d'obtenir 1,2,3,...,6 avec le second dé.
Notons S la variable aléatoire : somme des deux dés.
Notons [latex]p=\frac{1}{11}[/latex].
Par l'absurde, supposons qu'il existe des nombres réels [latex]a_1,a_2,...,a_6,b_1,b_2,...,b_6[/latex] dans [0;1] tels que :
[TeX]{P(S=2)=P(S=3)=...=P(S=12)=p}[/TeX]
D'une part, [latex]P(S=2)=P(S=12)=p[/latex] est équivalent à écrire que :
[TeX]a_1b_1=a_6b_6=p[/latex] Donc [latex]a_1b_6=\frac{p^2}{b_1a_6}[/TeX]
D'une autre part, [latex]P(S=7)=p[/latex] implique qu'il existe un réel s <p tel que :
[TeX] a_1b_6 + s + a_6b_1 = p [/latex] [latex](E)[/TeX]
Posons [latex]\mu=b_1a_6[/latex]
D'abord, [latex]\mu[/latex] est un réel strictement positif.
Ensuite, L'équation (E) devient [latex] \frac{p^2}{\mu} + s+ \mu = p [/latex]
Ce qui est équivalent à :
[TeX] \mu^2 +(s-p)\mu + p^2 = 0 [/TeX]
Absurde !! Car [latex]s<p[/latex] implique que ce polynôme de degré 2 en [latex]\mu[/latex] est de discriminant négatif et ne peut donc pas avoir une racine [latex]\mu[/latex] réelle positive.
#23 - 21-05-2011 13:03:54
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
Dés truqué
Pour tout le monde : avez pensez au cas où certaines probabilités sont nulles? Cela sera plus facile chez certains que chez d'autres.
Un mathématicien complet est topologiquement fermé!
#24 - 22-05-2011 01:30:31
- Alexander Bogomolny
- Visiteur
#25 - 22-05-2011 13:38:02
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Dés trqués
je peux deja dire qu'il est impossible de modifier 2 dés de maniere identique est d'avoir la meme probabilité d'apparition de chaque somme possible de 2 à 12.
Pour cela il faudrait que la probabilité du 1 et du 6 soit la meme pour avoir la meme probabilité d'avoir un 1+1 et un 6+6 et donc le 1+6 aurait une probabilité au moins double...
Il est donc necessaire que les dés soient truqués de maniere differente.
En modifiant les 2 des de maniere differente, le mieux que j'obtienne est ceci:
pour le dé numero 1:
probabilité de 1: 0.170702
probabilité de 2: 0.085463
probabilité de 3: 0.101788
probabilité de 4: 0.135718
probabilité de 5: 0.169647
probabilité de 6: 0.339294
pour le dé numero 2:
probabilité de 1: 0.339294
probabilité de 2: 0.169647
probabilité de 3: 0.135718
probabilité de 4: 0.101788
probabilité de 5: 0.085463
probabilité de 6: 0.170702
pour la somme des dés:
probabilite d'un 2: 0.057918
probabilite d'un 3: 0.057956
probabilite d'un 4: 0.072202
probabilite d'un 5: 0.092291
probabilite d'un 6: 0.117687
probabilite d'un 7: 0.209124
probabilite d'un 8: 0.117687
probabilite d'un 9: 0.092291
probabilite d'un 10: 0.072202
probabilite d'un 11: 0.057956
probabilite d'un 12: 0.057918
le rapport entre la probabilite d'un 7 par rapport a un 12: 3.6106909
a comparer avec les probabilités classiques:
pour faire un 2 ou un 12: 1/36 = 0.027777777
pour faire un 7: 1/6 = 0.166666667
avec un rapport de 6.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









