|
#26 - 03-01-2015 18:47:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteeau 87
Non Nodgim , là je ne comprends plus 
Vasimolo
#27 - 03-01-2015 19:24:35
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
gâtzau 87
Salut Vasimolo,
Je reprends un petit morceau de ton gâteau, ça fait longtemps que je n'y avais pas goûté.
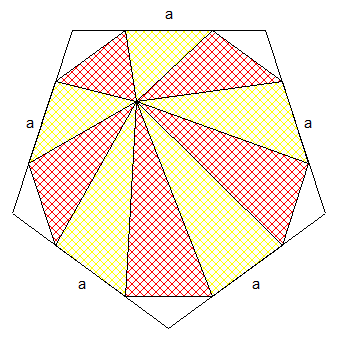
Si c est le côté du polygone et m la longueur de sa médiane, la somme des aires de deux parts opposées vaut :
ch/2 + cg/2 = c(h+g)/2 = cm/2 ( g et h sont les hauteurs respectives de ces deux triangles, donc h+g=m )
cm/2 est constant et ne dépend pas du point intérieur choisi.
Le partage est donc équitable 
#28 - 04-01-2015 06:04:49
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâetau 87
Oui je me suis planté, et même mon histoire de symétrie boîte....
On agrandit par prolongement les cotés rouges au détriment des cotés blancs jusqu'à les rejoindre et former un polygone à n cotés au lieu du 2n d'origine. Comme le polygone d'origine est régulier, tous les cotés sont agrandis dans un rapport de k, et donc le total de l'aire aussi, car chaque triangle rouge conserve sa hauteur, seule la base est uniformément agrandie dans un rapport de k.
Si l'aire rouge est R au départ elle devient kR
Si on fait la même chose pour les cotés blancs, pareil: aire B de départ devient kB.
Comme les 2 nouveaux polygones sont entièrement rouge pour l'un, blanc pour l'autre, et de même taille:
kR=kB d'où R=B les aires sont identiques au départ.
#29 - 04-01-2015 11:09:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtaeu 87
@Looozer : je ne comprends pas ton calcul , qu'appelles-tu médiane ?
@Nogim : je ne vois pas comment tu conclus avec l'une ou l'autre de tes deux idées . Exprime simplement l'aire rouge ou jaune dans tes polygones à n côtés .
Vasimolo
#30 - 04-01-2015 11:17:19
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
Gâteau 8
Pour ne pas embrouiller, j'ai mis de coté ma seconde idée. En revanche, je ne vois pas trop ce qu'il manque à la 1ère. J'ai ajouté une chose ou 2, mais ça me semble assez clair.
#31 - 04-01-2015 11:28:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteu 87
Oui , maintenant c'est clair 
Vasimolo
#32 - 04-01-2015 11:58:54
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3828
gâtzau 87
J'étais en train de me demander, lorsque le polygone est irrégulier, mais la longueur totale des cotés rouges est égale à la longueur totale des cotés blancs, quelle forme pouvait avoir la ligne des pts de concourance d'égalité entre les couleurs rouge et blanche. Sans doute une seule ligne, pas droite et qui rejoint obligatoirement les cotés (ne peut former une boucle) ?
#33 - 04-01-2015 12:20:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gteau 87
Ca a l'air intéressant mais on va attendre que le sujet soit visible par tous 
J'ai toujours trouvé particulièrement pénibles les "machins2" proposés à la communauté alors que "machin1" restait encore caché pendant plusieurs jours .
Vasimolo
#34 - 04-01-2015 16:32:10
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
gâtrau 87
J'appelle médiane le segment de droite joignant les milieux de deux côtés opposés.
#35 - 04-01-2015 17:33:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtea u87
Dans ce cas je ne vois pas pourquoi g+h=m entraîne que Somme{g} = Somme{h} ?
Vasimolo
#36 - 04-01-2015 18:57:03
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâteua 87
Tu as raison, je me suis à moitié trompé.
Partant d'un octogone, comme toi, j'ai vu que les parts opposées avaient même couleur et une somme des aires constante. Ce qui rend équitable le partage.
Hélas, ce n'est vrai que pour les polygones réguliers dont le nombre de côtés est multiple de 4. Dans les autres cas, les parts opposées sont de couleurs différentes.
Faut que je cherche encore...
Voici une autre idée :
1. Dans un polygone régulier donné, la somme des distances d'un point intérieur aux côtés est constante (théorème de Viviani)
2. Or, ces distances correspondent aux hauteurs des parts triangulaires découpées à partir de ce point intérieur.
3. Dans un polygone régulier ayant un nombre pair de côtés (2n), si l'on prolonge les côtés de rang pair (ou de rang impair) on obtient encore un polygone régulier à n côtés.
4. La somme S des distances du point intérieur aux côtés de ce polygone (et donc la somme des hauteurs des parts triangulaires de chacun des protagonistes) est constante (Voir 1.)
5. La part de chacun sera donc égale à la moitié du produit du demi-périmètre du gâteau et de cette constante S.
#37 - 04-01-2015 19:27:30
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gââteau 87
salut.
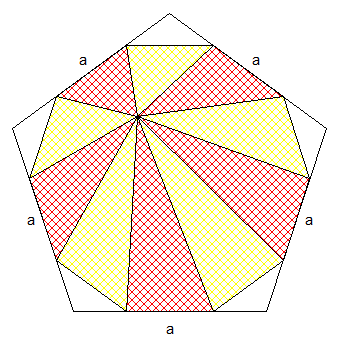
quelque soit la position du point P , la somme des hauteurs est constante et sur la figure à 10 côtés les 3 plus grandes hauteurs sont dans les triangles blancs c'est donc la partie blanche la plus importante .
#38 - 05-01-2015 17:34:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
#39 - 05-01-2015 22:25:48
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Gâteau 7
Génial, merci Vasimolo pour ce gâteau !
|
 |

 Accueil
Accueil
 Forum
Forum