|
#1 - 07-03-2015 19:06:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
#2 - 07-03-2015 22:15:41
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâteau 995
Si c'est pour dire à peu près 1/2 je suis d'accord. Maintenant, si c'est pour trouver la valeur exacte, il y a un calcul d'intégrale pas piqué des vers à sortir, et c'est pas pour moi...
#3 - 08-03-2015 00:03:22
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Gâteau 995
Par calculs relativement simples en prenant des rapport de surface, je trouve que le pourcentage où aucun joint n'est chevauché est :
minoré par: 31/27-4*racine(3)/9 = 0.378347789228647 et
majoré par : 28/27-2*racine(3)/9 = 0.652136857577287.
A partir d'un milliard de lancées aléatoires de gâteaux, mon petit code me donne les résultats suivants:
Cas où ça coupe un joint : 0.474116261
Cas où ça ne coupe aucun joint : 0.525883739
Reste à retrouver ces résultats par calcul d'ici la fin du temps imparti 
#4 - 08-03-2015 10:26:38
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâtea 95
@Nodgim : le calcul est un peu long mais surtout méticuleux , la seule intégrale à calculer est :

Le résultat s'obtient facilement avec un changement de variable et une intégration par partie .
@Kossi : j'ai une différence de 1 millième par rapport à ton résultat . J'ajouterai du temps au besoin 
Bon courage , c'est un peu laborieux mais le résultat exact est simple ( si je ne me suis pas trompé ) .
Vasimolo
#5 - 08-03-2015 10:53:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâtteau 95
Merci Vasimolo, mais je n'ai jamais fait ce genre de choses. Bon, je regarderai la solution avec plaisir.
@+
#6 - 10-03-2015 10:44:57
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâteau 995
Quand le barycentre du triangle équilatéral est éloigné de plus de (2/3).h = V3/3.c [respectivement de moins de (1/3).h = V3/6.c], alors il y a une probabilité de 100% [respectivement de 0%] que le gâteau ne chevauche aucun joint. Entre ces deux valeurs, je cherche toujours la fonction correspondante. Affaire à suivre ...
Edit: En approximant linéairement la zone intermédiaire, j’obtiens la valeur fausse de:
{(3-2.V3/3)².1 + [(3-V3/3)²-(3-2.V3/3)²].0,5 + [(3-V3/3)²-(3-2.V3/3)²].0} / 9
= [(31/3-4V3) + (V3-1/2)] / 9 = 59/54 - V3/3 = 0,5152 env.
#7 - 10-03-2015 19:54:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâteua 95
Je m'étais posé ce problème lorsque j'étais en terminale ( j'ai trouvé une solution l'année suivante ) quand j'ai découvert l'aiguille de Buffon .
L'approche de Franky était aussi la mienne ( à l'époque je n'avais pas de calculatrice et bien sûr pas d'ordinateur ) .
Vasimolo
#8 - 11-03-2015 19:29:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâetau 95
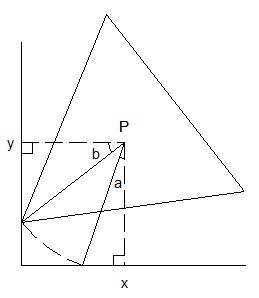
Je donne un petit indice visuel pour ceux que le calcul intéresse :
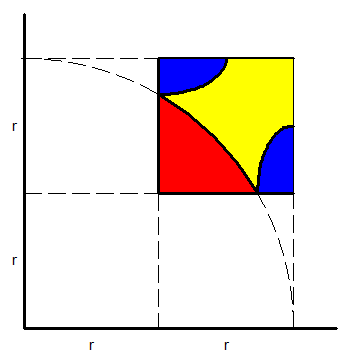
Voici un quart de maille de la paillasse :
J'ai choisi un triangle de côté 2 pour une maille de 6 , r est le rayon du cercle inscrit dans le triangle .
Vasimolo
#9 - 12-03-2015 17:31:49
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
hâteau 95
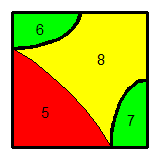
Le problème c'est ce sale petit carré numéroté "5". Une jolie courbe en forme de slip le partage en 5 zones, dont deux symétriques. Mais impossible de me dépatouiller de ces 5 intégrales ; je m'en sors pour deux d'entre elles, mais c'est tout.
Je suis également curieux de voir la solution, je dois avoir raté une astuce d'intégration.
#10 - 12-03-2015 17:58:37
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gtâeau 95
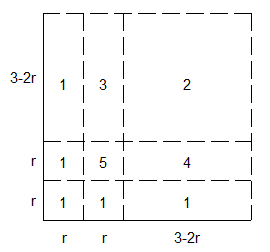
C'est en effet les zones 3 , 4 et 5 qui sont les plus délicates ( attention j'ai changé la numérotation du petit carré ) .
Les zones 1 et 2 ne posent aucun problème 
Vasimolo
#11 - 12-03-2015 19:13:11
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gâteau 59
Les zones 3 et 4 ne sont-elles pas les mêmes ? Je pensais qu'il y aurait une symétrie par rapport à la diagonale.
#12 - 12-03-2015 21:51:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
gâtrau 95
Oui, les zones sont symétriques par rapport à la diagonale . J'ai choisi deux noms différents car a intervient dans les zones 4 et 5 et b dans 3 et 5 .
Vasimolo
#13 - 14-03-2015 19:55:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâteau 59
J'ai repris mes calculs qui dataient de Mathusalem et il y a une erreur dans la zone 5 que je voyais découpée en quatre parties bordées par quatre segments et un douzième de cercle . Deux des segments sont en fait des quarts d'ellipses le calcul est donc "un peu" plus compliqué ( et explique sans-doute le millième d'écart avec Kossi ) . D'autre part je ballotte un peu dans le slip d'Echibu ( il me manque la partie basse ) , j'ai sans doute encore raté quelque chose 
Une illustration ?
Pour résumer : le problème est ouvert 
Vasimolo
#14 - 14-03-2015 20:27:01
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Gâteauu 95
Ok, vasimolo
Faut que je m'y remette 
#15 - 15-03-2015 12:37:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
#16 - 15-03-2015 15:35:55
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Gâtau 95
Si on donnait de la hauteur aux points en fonction du pourcentage d'échappement du triangle en rotation, ça doit donner une drôle de forme dans les angles: pas d'arêtes d'angle, que de l'arrondi.
#17 - 15-03-2015 17:41:31
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteaau 95
@Vasimolo
Ton dernier message m'a fait prendre conscience d'une erreur de ma part qui compliquait mes intégrales. Je vais donc retourner à mes calculs des fois que maintenant, ce soit possible.
Par contre, à voir ton dessin, j'ai l'impression qu'il y a aussi une erreur dans ton raisonnement. D'abord, je ne suis pas sûr de la forme des parties bleues, mais surtout, je pense qu'il manque une toute petite 5e zone, en haut à droite, où la proba serait plutôt (a+b)/60. Concrètement, c'est la zone où placer le centre du triangle pour qu'il ne soit jamais possible de couper en même temps les deux lignes, quelle que soit l'orientation du triangle.
C'est peut-être ça qui explique le millième manquant ?
#18 - 15-03-2015 18:04:52
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
gâtzau 95
Quand la distance du barycentre du triangle équilatéral au bord de cette grille est comprise entre (V3/6).c et (V3/3).c, alors le gâteau a une "liberté angulaire" de: pi/3-Arccos(x.V3/c), soit une proportion de: 1-Arccos(x.V3/c)/(pi/3)
J’intègre: 1-Arccos(x.V3/c)/(pi/3), entre (V3/6).c et (V3/3).c,
ce qui revient à intégrer: 1-Arccos(x)/(pi/3), entre 1/2 et 1,
ce qui donne: 1/2-[(pi/3)-V3/2]/(pi/3)=3V3/2.pi-1/2
Au final, j’obtiens une probabilité de:
{(3-2.V3/3)².1+[(3-V3/3)²-(3-2.V3/3)²].[3V3/2.pi-1/2]+[(3-V3/3)²-(3-2.V3/3)²].0}/9
=[(31/3-4V3)+(2V3-1).(3V3/2.pi-1/2)]/9=65/54-5V3/9+1/pi-V3/6.pi=0,467875 env.
#19 - 15-03-2015 18:28:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
#20 - 15-03-2015 19:09:42
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3222
- Lieu: Luxembourg
Gââteau 95
C'est la probabilité que le gâteau balancé ne chevauche aucun joint.
Mon erreur provient surement de la zone d'angle (la n°5).
Je vois à peu près comment corriger ça, mais je reviendrai demain.
Affaire à suivre ...
#21 - 15-03-2015 19:20:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâtea 95
Il est clair que cette zone 5 pose problème et je ne suis absolument pas convaincu qu'elle ne soit constituée que de 4 parties .
Vasimolo
#22 - 16-03-2015 14:38:15
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâtea u95
@Vasimolo : la zone 8 pose problème, puisque si on fait tendre un point vers le coin supérieur droit, la probabilité tend vers 1/4 au lieu de 0.
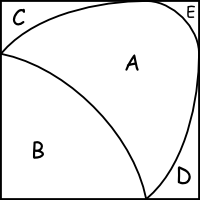
Voici à quoi ressemble ma case 5. Dans la zone E, il y a la proba (a+b)/60.
Sinon, j'ai enfin terminé mes intégrales. À la fin, je tombe sur une proba de Spoiler : [Afficher le message] 33/(18pi) - racine(3)/36 , mais les calculs sont tellement horribles que je serais surpris que ce soit juste.
#23 - 16-03-2015 20:32:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,427E+3
Gâteau 59
Beau travail Echibu 
Je suis d'accord avec ton découpage ( je n'avais pas vu que dans la partie E le triangle décollait deux fois des joints dans sa rotation de 120° ) .
La bordure des parts C et D sont des quarts d’ellipse , celle de B est un arc de cercle . Je pense que le bord de E est aussi un arc de cercle mais je n'ai pas encore pris le temps de vérifier .
Le calcul des intégrales dans les parties C et D est sûrement la plus délicate .
A suivre ...
Vasimolo
PS : j'ai du mal à croire en ta formule mais je peux me tromper .
#24 - 16-03-2015 21:33:51
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâyeau 95
D'après mes calculs, la frontière entre A et B est effectivement un arc de cercle centré sur l'intersection du quadrillage. Quant aux autres frontières (entre A et C, D, E), il s'agit d'une seule et même courbe, un morceau d'ellipse tournée à 45°, et elle aussi centrée sur l'intersection du quadrillage.
Pour vérification, je soumets les contributions de chaque morceau à la probabilité totale :
* zones de type 1 : Spoiler : [Afficher le message] \frac{2\sqrt{3}}{9}-\frac{1}{27}
* zones de type 3 et 4 : Spoiler : [Afficher le message] \frac{2}{\pi}-\frac{2\sqrt{3}}{9}-\frac{4\sqrt{3}}{9\pi}+\frac{4}{27}
* 4 zones B : Spoiler : [Afficher le message] \frac{1}{27}-\frac{\sqrt{3}}{27}+\frac{\pi}{81}
* 4 zones de chaque type C, D, E : Spoiler : [Afficher le message] -\frac{4}{27}+\frac{4\sqrt{3}}{9\pi}-\frac{1}{6\pi}-\frac{\pi}{81}
* 4 zones de type A : Spoiler : [Afficher le message] \frac{\sqrt{3}}{108}
* total : Spoiler : [Afficher le message] \frac{11}{6\pi}-\frac{\sqrt{3}}{36}
#25 - 16-03-2015 22:14:17
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
gâtrau 95
Une grosse boulette dans mon code, un signe moins qui traiait à un endroit où il n'a rien à y faire 
J'écrivais ceci:
A partir d'un milliard de lancées aléatoires de gâteaux, mon petit code me donne les résultats suivants:
Cas où ça coupe un joint : 0.474116261
Cas où ça ne coupe aucun joint : 0.525883739
ce résultat est donc erroné. mea maxima culpa   
Après une bonne vérification et toujours sur le milliard de lancées aléatoires, je trouve ceci:
Cas où ca coupe : 0.535469636
Cas où ca ne coupe pas : 0.464530364
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum