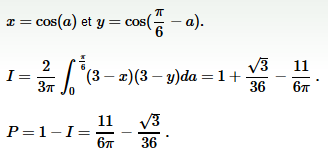|
#26 - 16-03-2015 22:33:17
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâteay 95
@kossi_tg
J'avais des doutes sur ton ancien calcul, je ne voyais pas comment il était possible de trouver une proba que ça coupe inférieure à 1/2.
Ton nouveau calcul confirme le mien, merci, je suis beaucoup plus convaincu de sa validité désormais.
#27 - 16-03-2015 22:42:01
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
GGâteau 95
Voici le code en java pour ceux que cela pourrait intéresser:
Spoiler : [Afficher le message] public class PaillasseGateau {
static double pi=Math.PI;
public static void main(String[] args) {
double a=Math.sqrt(3.0), n=1E9, c=3.0*a, h=0.5*Math.sqrt(3.0)*a, r=h/3.0, cpn=0.0, cp=0.0;
for(int i=0;i*1.0<n;i++){
double x=c*Math.random(), y=c*Math.random(); // choix aléatoire du centre du cercle insrit noté O
double al=(2*pi)*Math.random(); // choix aléatoire de l'angle de fait le vecteur OB avec l'axe des x
double xOB=2.0*r*Math.cos(al), yOB=2.0*r*Math.sin(al); // les coordonnées du vecteur OB sachant que ||OB||=2*r
//calcul des coordonnées des vecteurs OA et OC par rotation resp. de 2*ip/3 de OB et OA
double co=Math.cos(2.0*pi/3.0), si=Math.sin(2.0*pi/3.0), xOA=co*xOB-si*yOB, yOA=si*xOB+co*yOB, xOC=co*xOA-si*yOA, yOC=si*xOA+co*yOA;
//déduction des coordonnées de A, B et C.
double xC=xOC+x, yC=yOC+y,xB=xOB+x, yB=yOB+y, xA=xOA+x, yA=yOA+y;
// test sur A, B et C, si au moins des 3 est à l'extérieur de la maille, cp est incrémenté de 1
if(!interne(c,xA,yA)||!interne(c,xB,yB)||!interne(c,xC,yC)){
cp+=1.0;
}
}
//calcul des parts en divisant cp et n-cp par le nombre de tirage qui est n
double pro=cp*1.0/n , pri=(n-cp)/n;
System.out.println("Cas où ca coupe : "+pro);
System.out.println("Cas où ca ne coupe pas : "+pri);
}
//cette méthode prend le coté de la maille et les coordonnées d'un point M(xm,ym) et teste si ce point est à l'intérieur ou pas de la maille
private static boolean interne(double c, double xm, double ym){
boolean ret=true;
if(xm<=0.0 || ym<=0.0 || xm>=c || ym>=c){
ret=false;
}
return ret;
}
}
Pour le confort de lecture, je mets une capture d'écran à ce lien:
http://www.prise2tete.fr/upload/kossi_tg-Paillasses.png
J'ai mis le lien car l'affichage en photo n'est pas génial.
Je dirais BIGO au résultat d'Ebichu pour le coup 
.
#28 - 16-03-2015 23:04:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâtau 95
L'ellipse unique et l'arc de cercle , je suis convaincu 
Pour les calculs , il faudra que je trouve un peu de temps pour vérifier , ce qui va être très dur en ce moment mais je ne lâche pas le morceau .
L'absence de LaTeX est toujours aussi pénible 
Vasimolo
#29 - 17-03-2015 19:45:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gâteauu 95
Je vais avoir très peu de temps libre durant les trois semaines à venir mais je reviendrai sur le problème plus tard 
Il est clair que l'intérieur des différentes zones de la case 5 est parfaitement défini par des inégalités sur les angles a et b , idem pour la probabilité que le triangle touche les joints . En bref on doit pouvoir travailler directement sur les angles plutôt que sur les coordonnées cartésiennes ce qui devrait alléger fortement les calculs .
A bientôt 
Vasimolo
#30 - 21-03-2015 11:57:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâtzau 95
Il y a bien une approche simple du problème qui m'a été soufflée car je restais empêtré dans mes ellipses et autres arc cosinus ...
On note a ( entre 0° et 30° ) l'angle formé par un côté du triangle avec l'horizontale et on inscrit le triangle dans un rectangle dont les côtés sont parallèles aux mailles .
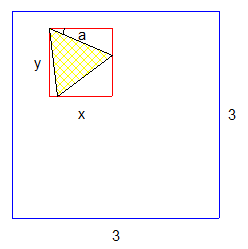
Le triangle ne touche aucune ligne si et seulement si son centre se situe dans un rectangle de côtés 3-x et 3-y .
La probabilité I pour qu'il ne traverse aucun joint ou P pour qu'il en traverse au moins un peut alors se calculer très facilement :
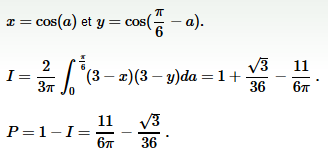
Vasimolo
#31 - 22-03-2015 18:06:47
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
gâyeau 95
Effectivement : fixer l'angle, puis déterminer les coordonnées qui conviennent, est incomparablement plus efficace que fixer les coordonnées, puis déterminer les angles qui conviennent. Les calculs sont au moins 10 fois plus rapides. La différence de complexité entre les deux méthodes est vraiment surprenante 
Intuitivement, on a tendance à se diriger vers la deuxième façon de faire et à se compliquer la vie. C'est là la plus grosse difficulté de ce problème, et c'est une bonne leçon.
#32 - 23-03-2015 20:28:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
Gteau 95
Une remarque : dans le problème proposé on jette un triangle équilatéral de périmètre 1 sur une paillasse de maille 1 . Que se passe-t-il si on jette un polygone régulier à n côtés et de périmètre 1 sur la même paillasse ? Et si on fait tendre n vers l'infini ?
Vasimolo
#33 - 24-03-2015 08:11:57
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
gâteai 95
Pour n infini, là c'est tout de suite plus facile, je crois.
#34 - 24-03-2015 09:35:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,447E+3
gâyeau 95
Oui , à l'infini le polygone est un cercle et la probabilité pour qu'il ne touche pas les lignes est (1-1/pi)² . Le cas n quelconque semble beaucoup plus compliqué car les côtés du rectangle enfermant le polygone dépendent de plusieurs cosinus .
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum