|
#1 - 25-10-2015 10:50:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#2 - 25-10-2015 11:05:57
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
gâtezu 109
Plusieurs solutions toutes de la forme: 4^N, avec N entier.
#3 - 25-10-2015 11:55:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâtaeu 109
Il n'y a qu'une solution Franky 
Vasimolo
#4 - 25-10-2015 12:22:15
- Moriss
- Professionnel de Prise2Tete
- Enigmes résolues : 37
- Messages : 460
Gâeau 109
Ils n'étaient pas 4 modulo 3, sinon il aurait réussi son défi.
Je vais me pencher un peu plus sérieusement sur le pb.
EDIT :
J'explique ma démarche.
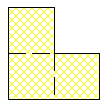
Le "L" ne peut être divisé qu'en 4.
Mais chaque part peut être sub-divisée elle-même en 4. La part sub-divisée ne compte plus mais on compte les 4 parts qu'on a faites avec elle. Donc le nombre total de parts est augmenté de -1+4 = 3.
Donc on peut découper 4 parts, 7, 10, etc. Soit 4 (mod3) parts possibles.
Donc, s'il y a n participants et que n = 4(mod3), alors on fait 1 part par personne.
Si n <> 4(mod3), alors on fait un grand nombre de parts tel que ce nombre ait n parmi ses facteurs possibles.
Exemple : 2 participants. On ne peut pas faire 2 parts. Pas grave, on en fait 4 (car 2 factorise 4) et on en donne 2 à chacun.
5 participants : on fait 10 parts, on en donne 2 à chacun.
Etc.
Le seul nombre de participant pour lequel on ne trouvera jamais un multiple dans 4(mod3) c'est justement 3. En effet, le nombre de part est égal à tous les multiples de 3 augmentés de 1, jamais à ces multiples eux-mêmes.
Il y avait donc 3 participants.
Oui mais, oui mais... Avec cette stratégie, tout le monde n'a pas forcément la même quantité de gâteau... 
#5 - 25-10-2015 13:53:50
- PvD47
- Habitué de Prise2Tete
- Enigmes résolues : 20
- Messages : 19
#6 - 25-10-2015 14:55:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
âteau 109
Pas de bonne réponse pour le moment 
Je précise que les parts ne sont pas nécessairement toutes de la même taille mais elles doivent être une réplique exacte du gâteau ( ie: une réduction ) .
Bon courage .
Vasimolo
#7 - 25-10-2015 15:16:06
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 1009
On considère un gâteau en L constitué de 3 carrés ou n'était-ce qu'un exemple ?
#8 - 25-10-2015 15:18:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâreau 109
Le "L" est forcément formé de 3 carrés et donc même chose pour les différentes parts .
Vasimolo
#9 - 25-10-2015 15:21:21
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3230
- Lieu: Luxembourg
Gtâeau 109
Avec 4^N, je pensais à ça:
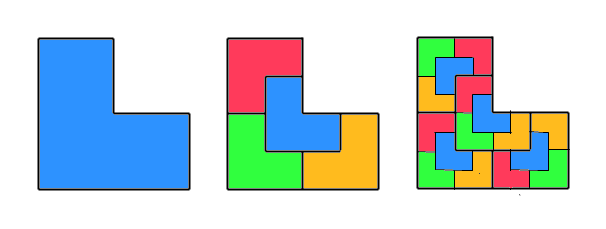
#10 - 25-10-2015 15:26:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteu 109
Je l'avais bien vu comme ça Franky : le but est de trouver un nombre de parts pour lequel le partage du triangle est possible mais pas celui du "L" .
Vasimolo
#11 - 25-10-2015 15:53:46
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâteau 09
Avec les triangles, je peux faire toutes le sommes de 2 impairs dont 1, et les mêmes +3, 6 9 12 ... .
A priori, je ne vois que 2 et 3 qui soient impossibles. EDIT : et 5
Avec le carré : On peut faire tous les multiples de 4 modulo 3 6 9 12 ...
Ca ne laisse que 6 ? ou 8 ? mais alors pour faire 6, c'est coton, je ne vois pas...
#12 - 25-10-2015 15:59:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteeau 109
Il te manque un cas d'impossibilité pour le triangle et la réponse n'est pas la bonne 
Vasimolo
#13 - 25-10-2015 17:46:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteua 109
@Gwen : il faut partir d'un découpage tout neuf ( pas d'un redécoupage d'un partage existant ) , sans oublier que les parts peuvent être de tailles différentes .
Vasimolo
PS : quand tu parles du carré du veux dire du L ?
#14 - 25-10-2015 18:26:40
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
Gâteauu 109
Oui le L et avec le triangle, comme pour le L on peut faire +3 par récurrence. Donc je pars d'un partage existant si je veux pour raisonner.
#15 - 25-10-2015 18:32:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteeau 109
D'accord , il faut donc que tu trouves un nouveau partage "primaire" du "L" .
Vasimolo
#16 - 25-10-2015 18:57:13
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Gâteau 19
Théorème trivial tous les triangles sont sécables en un nombre indéfini de plus petits triangles. Il reste à trouver pour les L 
Pour le moment je trouve pas de possibilité de faire 13 parts avec des L.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#17 - 25-10-2015 19:54:45
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteeau 109
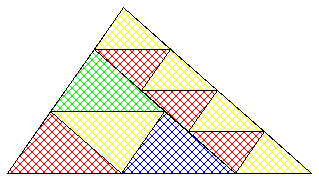
On sait partager le triangle en 1+3x+5y+7z+... parts triangulaires.
Les seules configurations impossibles sont 2, 3, 5.
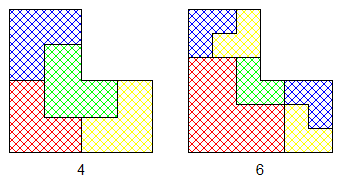
On sait partager le L initial en 1, 4, 9, 16, etc... parts égales.
http://www2.stetson.edu/~efriedma/LinL/
Parmi ces parts égales, une ou plusieurs peuvent à leur tour être partagées de la même façon, donnant 3x et/ou 8y et/ou 15z etc... parts supplémentaires.
On ne sait pas faire 6 ni 8, ni 11, ni 13, alors qu'on peut avec des triangles.
#18 - 25-10-2015 20:14:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
GGâteau 109
@Shadock : on peut faire avec 13 .
@Halloduda : on n'impose pas aux parts d'avoir la même taille .
Vasimolo
#19 - 26-10-2015 08:21:15
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
gâteai 109
Pour les triangles:
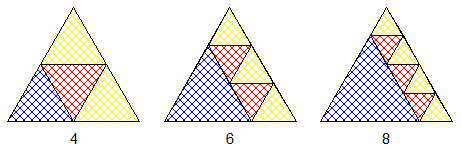
On partage le triangle en bandes parallèles à la base et toutes d'égale épaisseur.
Avec 2 bandes, on découpe en 1+3 triangles. Et comme chaque triangle peut lui même être remplacé par 4 autres triangles, on peut découper en 4+3k triangles.
Avec 3 bandes:1+3+5, mais on peut grouper 1+3 en 1 donc 6, puis 6+3k.
Avec 4 bandes: 1+3+5+7, mais en groupant 1+3+5 en 1 , donc 8, donc 8 + 3k.
4+3k, 6+3k et 8+3k peut être ramené 1,2, ou 3 modulo 3 , c'est à dire tous les entiers à partir de 6.
Pour les L j'ai une question: s'agit il d'un trimono (3 carrés accolés) ou la forme du L est elle libre ?
#20 - 26-10-2015 09:38:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
gâreau 109
C'est bon pour le triangle et oui les L sont nécessairement formés de trois carrés identiques comme sur le modèle .
Pour le moment seul Gwen a mis le doigt sur la solution mais il lui manque encore une pièce .
Bon courage à tous 
Vasimolo
#21 - 26-10-2015 15:51:00
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,039E+3
gâreau 109
Avec les triangles comme avec les L on peut faire +3 ou +5
Cela permet d'atteindre
1
4 (1+3)
6 (1+5)
7 (4+3)
9 (6+3)
10 (7+3)
11 (6+5)
et la suite de manière évidente modulo 3.
Il manque 2, 3 , 5 et 8.
2, 3 et 5 semble inatteignables avec des triangles comme avec des carrés (à moins d'un triangle rectangle isocèle). Mais 8 peut être atteint avec une bande de 7 triangles semblables, seulement dans le cas des triangles.

#22 - 26-10-2015 18:51:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
Gâteau 1109
C'est ça Gwen et en effet j'aurais dû préciser que le gâteau de l'an dernier n'était pas isocèle-rectangle : bravo !
Vasimolo
#23 - 28-10-2015 11:57:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3814
Gââteau 109
Bravo à Gwen, c'est bien le meilleur.
Il reste cependant à fabriquer un L avec 11 L pour l'unicité de la solution.
On sait que les solutions pour L sont 4+3k et 6+3k. On n'a pas le 8+3k comme pour le triangle.
#24 - 28-10-2015 12:04:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
#25 - 28-10-2015 12:13:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,433E+3
âGteau 109
@Nodgim : 6+5=11 
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum