Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#26 - 27-09-2016 08:44:23
Nomrbes serrésOK, Ebichu. Ce n'est pas destructeur du tout, c'est ce que je redoutais vaguement, mais sans pouvoir construire un tel contre-exemple, sans même savoir si ça pouvait exister. La preuve avancée est donc un beau sophisme ! #0 Pub#27 - 27-09-2016 12:33:06#28 - 27-09-2016 14:45:02
Nombres serréés1, 2, 4, 6, 8, 9, 12, 15, 18, 16, 20, 24, 28, 32, 25, 30, 35, 40, 45, 50, 36, 42, 48, 54, 60, 66, 72, 49, 56, 63, 70, 77, 84, 91, 98, 64, 72, 80, 88, 96, 81, 90, 99, 100 #29 - 27-09-2016 15:36:24
Noombres serrésIl faudrait revoir les definitions : #30 - 27-09-2016 17:33:36
Nombrse serrésUne donnée intéressante. #31 - 28-09-2016 22:44:51
Nmbres serrésPuisque la demonstration de tendre vers Zéro ne tient plus, on peut encore supposer (esperer?) que la densité des nombres serrés ne tend effectivement pas vers zéro. Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #32 - 29-09-2016 00:47:54
Nobmres serrésUn nombre de la forme 2k(k+1) reste serre a l`infini. #33 - 29-09-2016 08:10:52#34 - 29-09-2016 08:49:46
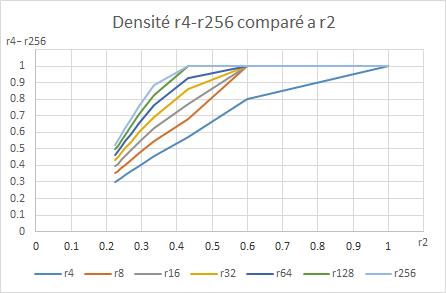
Nombres serrsAutre chose sur le second tableau: la courbe r4, en la projetant en ligne droite, est clairement coupée par les autres lignes. Ce qui est impossible. Il faut donc s'attendre à un brusque changement de courbe. Peut être même que le point de convergence est donc bien plus tôt que le 0,1. Ce pourrait être plus proche de 0,2. #35 - 29-09-2016 11:04:19
Nmbres serrésAprès réflexion, ce second tableau m'inspire autre chose. #36 - 29-09-2016 13:24:43
nombrzs serrésJe crois que pour que la limite tende vers 1, il faut changer un peu l'énoncé. Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #37 - 29-09-2016 15:16:17
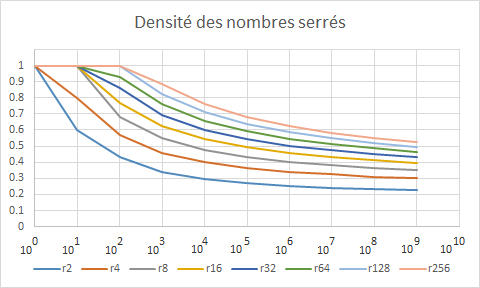
Nombre sserrésVoici les données réelles avec lesquelles j'ai fait les courbes: Code:10^0 1 1 1 1 1 1 1 1 1 10^1 3 6 8 10 10 10 10 10 10 10^2 10 43 57 68 77 86 93 100 100 10^3 31 336 455 547 624 692 762 822 886 10^4 100 2932 3985 4759 5415 6007 6570 7106 7608 10^5 316 26870 36406 43311 49131 54340 59120 63687 68067 10^6 1000 252756 340887 403836 456429 503193 546006 586034 624345 10^7 3162 2409731 3235797 3820725 4306486 4734660 5125341 5487449 5829598 10^8 10000 23169860 30994196 36497122 41035968 45009982 48626915 51973356 55114235 10^9 31622 224059958 298722912 350883783 393743606 431111287 464928289 496179897 525431229 et voici les données preliminaires sur une echelle logarithmic basée sur 2: Code:2^0 1 1 1 1 1 1 1 1 1 1 1 2^1 1 2 2 2 2 2 2 2 2 2 2 2^2 2 3 4 4 4 4 4 4 4 4 4 2^3 2 5 6 8 8 8 8 8 8 8 8 2^4 4 9 12 14 16 16 16 16 16 16 16 2^5 5 16 21 25 27 32 32 32 32 32 32 2^6 8 29 38 45 52 57 64 64 64 64 64 2^7 11 52 70 85 96 108 115 128 128 128 128 2^8 16 97 132 157 180 200 220 233 256 256 256 2^9 22 181 246 294 337 375 410 446 469 512 512 2^10 32 343 464 559 639 708 779 840 906 949 1024 2^11 45 652 890 1068 1214 1350 1479 1605 1718 1836 1911 2^12 64 1256 1713 2044 2330 2589 2837 3065 3291 3492 3704 2^13 90 2427 3297 3939 4483 4978 5441 5886 6299 6713 7081 2^14 128 4701 6387 7622 8670 9607 10496 11333 12150 12904 13655 2^15 181 9148 12416 14800 16809 18616 20304 21924 23456 24936 26323 2^16 256 17861 24212 28811 32696 36186 39416 42492 45440 48251 50974 2^17 362 34946 47323 56221 63754 70503 76683 82574 88209 93637 98826 2^18 512 68522 92632 110006 124586 137600 149534 160816 171668 182072 192110 2^19 724 134562 181719 215561 243877 269036 292137 313841 334692 354731 374036 2^20 1024 264705 357018 422946 477979 526912 571704 613572 653668 692285 729602 2^21 1448 521401 702134 830854 938183 1033384 1120444 1201391 1278675 1353285 1425426 2^22 2048 1027859 1382321 1634153 1843818 2029185 2198419 2355608 2504899 2649167 2788640 2^23 2896 2028019 2724099 3217604 3627434 3988532 4318220 4624151 4913572 5192483 5462382 2^24 4096 4004729 5373100 6340748 7142363 7847267 8490547 9087282 9649262 10189059 10712435 pour aller jusqu'a 2^31, ca prendra plus de 60 heures de calculs... Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #38 - 29-09-2016 17:46:40#39 - 29-09-2016 17:51:01#40 - 03-10-2016 15:16:50
nomnres serrésApres 90 heures de calculs, j'ai finalement atteint 2^31. Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #41 - 03-10-2016 16:35:51#42 - 03-10-2016 22:17:19
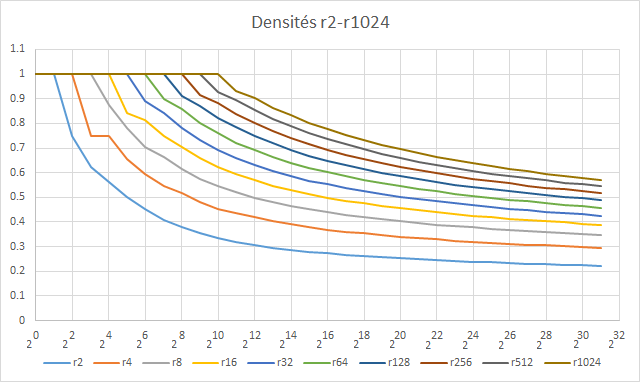
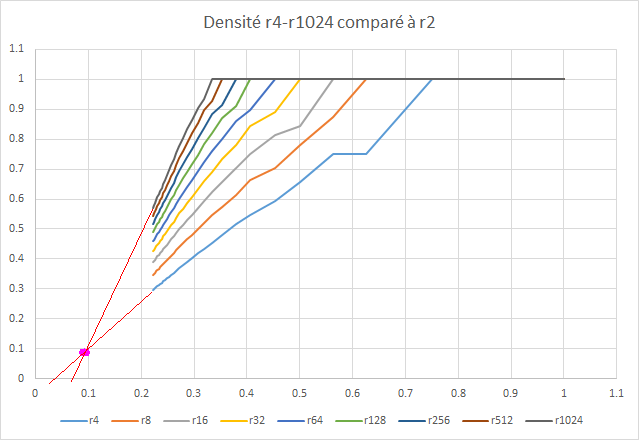
Nmbres serrésVoila déjà les résulats numériques: Code:2^0 1 1 1 1 1 1 1 1 1 1 1 2^1 1 2 2 2 2 2 2 2 2 2 2 2^2 2 3 4 4 4 4 4 4 4 4 4 2^3 2 5 6 8 8 8 8 8 8 8 8 2^4 4 9 12 14 16 16 16 16 16 16 16 2^5 5 16 21 25 27 32 32 32 32 32 32 2^6 8 29 38 45 52 57 64 64 64 64 64 2^7 11 52 70 85 96 108 115 128 128 128 128 2^8 16 97 132 157 180 200 220 233 256 256 256 2^9 22 181 246 294 337 375 410 446 469 512 512 2^10 32 343 464 559 639 708 779 840 906 949 1024 2^11 45 652 890 1068 1214 1350 1479 1605 1718 1836 1911 2^12 64 1256 1713 2044 2330 2589 2837 3065 3291 3492 3704 2^13 90 2427 3297 3939 4483 4978 5441 5886 6299 6713 7081 2^14 128 4701 6387 7622 8670 9607 10496 11333 12150 12904 13655 2^15 181 9148 12416 14800 16809 18616 20304 21924 23456 24936 26323 2^16 256 17861 24212 28811 32696 36186 39416 42492 45440 48251 50974 2^17 362 34946 47323 56221 63754 70503 76683 82574 88209 93637 98826 2^18 512 68522 92632 110006 124586 137600 149534 160816 171668 182072 192110 2^19 724 134562 181719 215561 243877 269036 292137 313841 334692 354731 374036 2^20 1024 264705 357018 422946 477979 526912 571704 613572 653668 692285 729602 2^21 1448 521401 702134 830854 938183 1033384 1120444 1201391 1278675 1353285 1425426 2^22 2048 1027859 1382321 1634153 1843818 2029185 2198419 2355608 2504899 2649167 2788640 2^23 2896 2028019 2724099 3217604 3627434 3988532 4318220 4624151 4913572 5192483 5462382 2^24 4096 4004729 5373100 6340748 7142363 7847267 8490547 9087282 9649262 10189059 10712435 2^25 5792 7913696 10605736 12503799 14074126 15452814 16710217 17873973 18968369 20015444 21030745 2^26 8192 15648166 20945873 24674407 27753872 30454733 32912248 35185333 37321603 39356567 41328281 2^27 11585 30956618 41391477 48721757 54769828 60060244 64867734 69317238 73490808 77456886 81288116 2^28 16384 61270396 81839243 96264952 108143233 118519325 127938355 136651268 144818542 152563411 160014184 2^29 23170 121326262 161898427 190292716 213640942 234020841 252487337 269564551 285559925 300704209 315228442 2^30 32768 240351455 320410652 376332077 422277455 462328162 498570611 532062390 563407776 593068498 621440415 2^31 46340 476311400 634364179 744605630 835045490 913821933 985008325 1050716884 1112229904 1170365055 1225892663 Pour les courbes... à suivre... Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #43 - 04-10-2016 00:10:26#44 - 04-10-2016 08:42:22
Nombres serréésOK Dhrm. #45 - 09-10-2016 09:06:01
Nombres serérsUn "a" donné génère (a+1)(a+2)/2 nombres serrés dans l'intervalle [a^2; 4a^2] #46 - 11-10-2016 13:39:42#47 - 11-10-2016 16:46:43#48 - 11-10-2016 16:56:18
Nobmres serrésUn "a" donné génère (a+1)(a+2)/2 nombres serrés dans l'intervalle [a^2; 4a^2] Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.